数学分析笔记3：函数的极限

函数极限的定义与性质

定义3.1 (1) $f(x)$在 $x_0$的某个去心邻域上有定义，若存在实数 $A$，对任意的 $\varepsilon>0$，存在正数 $\delta>0$，当 $0<|x-x_0|<\delta$时，都有 $|f(x)-A|<\varepsilon$则称函数 $f(x)$在 $x_0$处极限存在，A是 $f(x)$在 $x_0$处的极限，记为 $\lim_{x\to{x_0}}{f(x)}=A$
(2)如果对任意的正数 $M>0$，存在正数 $\delta>0$，当 $0<|x-x_0|<\delta$时，有 $f(x)>M(<-M)$则称函数 $f(x)$是 $x_0$处的正(负)无穷大量，记为 $\lim_{x\to{x_0}}{f(x)}=+\infty(-\infty)$
(3)如果 $|f(x)|$是 $x_0$处的正无穷大量，则称 $f(x)$是 $x_0$处的无穷大量

除了定义某个点的极限，还可以定义趋于无穷的极限
定义3.2 (1) $f(x)$在 $(a,+\infty)((-\infty,a))$上有定义，若存在实数 $A$，对任意的 $\varepsilon>0$，存在正数 $M>0$，当 $x>M(<-M)$时，都有 $|f(x)-A|<\varepsilon$则称函数 $f(x)$在 $x\to +\infty(\to -\infty)$的过程极限存在，A是 $f(x)$在过程 $x\to +\infty(\to -\infty)$的极限，记为 $\lim_{x\to +\infty}{f(x)}=A(\lim_{x\to -\infty}{f(x)}=A)$
(2)如果对任意的正数 $M>0$，存在正数 $M_2>0$，当 $x>M_2(x<-M_2)$时，都有 $|f(x)|\ge M$则称函数 $f(x)$是 $x\to +\infty(\to -\infty)$过程的正无穷大量，记为 $\lim_{x\to +\infty}{f(x)}=+\infty(\lim_{x\to -\infty}{f(x)}=+\infty)$
(3)如果对任意的正数 $M>0$，存在正数 $M_2>0$，当 $x>M_2(x<-M_2)$时，都有 $|f(x)|\le -M$则称函数 $f(x)$是 $x\to +\infty(\to -\infty)$过程的负无穷大量，记为 $\lim_{x\to +\infty}{f(x)}=-\infty(\lim_{x\to -\infty}{f(x)}=-\infty)$
(4)如果 $|f(x)|$是 $x\to +\infty(\to -\infty)$过程的正无穷大量，则称 $f(x)$是 $x\to +\infty(\to -\infty)$过程的无穷大量

这样，对函数而言，有三种趋近过程，如果考虑广义极限，还有三种极限（有限实数、正负无穷），三种过程有三种无穷小量，三种无穷大量，这是和数列极限的区别。下面我们考虑收敛于有限实数的情形，我们统一记成 $\lim{f(x)}$，统一给出性质，当然，这些性质的证明和数列情形是类似的，这里我们就不给出具体的证明过程。
定理3.1
(1)函数极限是唯一的
(2)(局部有界性)函数 $f(x)$在某个过程的极限存在，那么在某个时刻之后函数是有界的
(3)(不等式性质)函数 $f(x)$和 $g(x)$在某个过程的极限存在，并且存在某个时刻，在该时刻之后，有 $f(x)\le{g(x)}$，则 $\lim{f(x)}\le\lim{g(x)}$
(4)(不等式性质2)函数 $f(x)$和 $g(x)$在某个过程的极限存在，并且 $\lim{f(x)}<\lim{g(x)}$，则存在某个时刻，在该时刻之后，有 $f(x)<{g(x)}$
(5)(局部保号性1)函数 $f(x)$在某个过程的极限存在，在某个时刻之后，有 $f(x)\le 0(\ge 0)$，则 $\lim{f(x)}\le 0(\lim{f(x)}\ge 0)$
(6)(局部保号性2)函数 $f(x)$在某个过程的极限存在， $\lim{f(x)}> 0(\lim{f(x)}< 0)$，则在某个时刻之后，有 $f(x)> 0(<0)$
(7)函数极限的四则运算性质都成立
(8)(夹逼准则)函数 $f(x)$和 $g(x)$在某个过程的极限都等于 $A$，并且在该过程的某个时刻之后，都有 $f(x)\le h(x) \le g(x)$，则 $h(x)$在该过程的极限存在，并且 $\lim{h(x)}=A$

所谓某个时刻，我们可以列表加以说明

过程	"在某个时刻之后"的含义
$\lim_{x\to x_0}$	$\exist \delta>0$,当 $0<$| $x-x_0$| $<\delta$时
$\lim_{x\to +\infty}$	$\exist M>0$,当 $x>M$时
$\lim_{x\to -\infty}$	$\exist M>0$,当 $x<-M$时
$\lim_{x\to \infty}$	$\exist M>0$,当 $x>$| $x$|时

无穷小量和无穷大量也有类似的性质
定理3.2
(1) $f(x)$是某个过程的无穷小量， $g(x)$是该过程中某个时刻之后的有界变量，则 $f(x)g(x)$是该过程的无穷小量
(2) $\lim{f(x)}=A$的充要条件是 $f(x)-A$是该过程的无穷小量
(3) $f(x)$是该过程的无穷小量的充分必要条件是 $\frac{1}{f(x)}$是该过程的无穷大量
(4) $f(x)$是某个过程的无穷大量(正无穷大量、负无穷大量)， $g(x)$是该过程中某个时刻之后的有界变量，则 $f(x)\pm g(x)$是该过程的无穷大量(正无穷大量、负无穷大量)
(5) $f(x)$是某个过程的无穷大量，存在正数 $m>0$， $g(x)$在该过程的某个时刻之后满足 $|g(x)|>m$，则 $f(x)g(x)$是该过程的无穷大量
(6)两个正(负)无穷大量的和还是正(负)无穷大量
(7)正(负)无穷大量和负(正)无穷大量的差是正(负)无穷大量

下面，我们对函数极限的无穷大量和无穷小量的阶作一个统一的定义：
定义3.3
$f(x)$和 $g(x)$是某个过程的两个无穷小量
(1)如果 $\lim{\frac{f(x)}{g(x)}}=0$，则称 $f(x)$是 $g(x)$的高阶无穷小，记为 $f(x)=o(g(x))$
(2)如果 $\lim{\frac{f(x)}{g(x)}}=A\neq 0$，则称 $f(x)$和 $g(x)$是同阶无穷小
(3)如果 $\lim{\frac{f(x)}{g(x)}}=1$，则称 $f(x)$和 $g(x)$是等价无穷小

作为函数极限的例子，我们来证明一个重要的极限：
例3.1 $\lim_{x\to 0}{\frac{\sin(x)}{x}}=1$

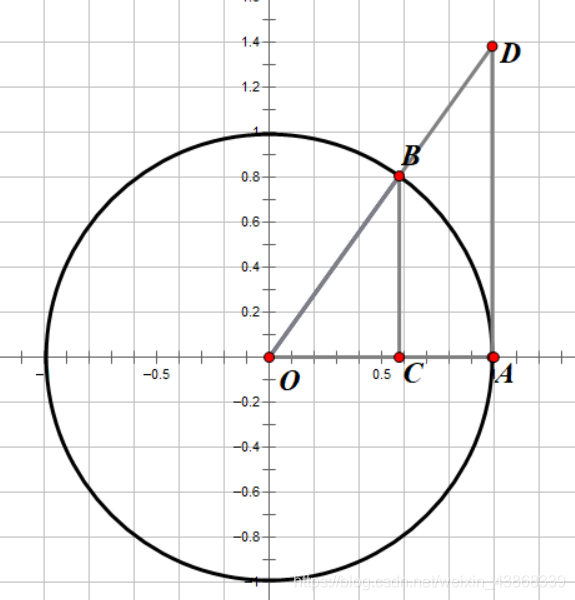
证：
实际上，由几何关系，在 $0<x<\frac{\pi}{2}$时，有 $\sin(x)<x<\tan(x)$在三角形 $\triangle ABC$中， $|BC|=\sin(x) < |AB|$,而两点之间线段最短，因此 $|AB|$又比弧长 $x$小，因此，有 $\sin(x)<x$，而扇形的面积小于 $\triangle OAD$的面积，就直接有 $x<\tan(x)$为了应用夹逼准则，我们还要证明 $\lim_{x\to 0}{\cos(x)}=1$考察 $|\cos{x}-1|=|2\sin(\frac{x}{2})^2|\le{\frac{x^2}{2}}$
再由夹逼准则，有 $\lim_{x\to 0}{\cos(x)}=1$同时，有以下不等式 $\frac{1}{\cos{x}} < \frac{\sin{x}}{x} < 1$（注意到 $\frac{\sin{x}}{x}$是偶函数)
再应用夹逼准则可以证得结论

在这里，我们再引入两个极限过程：
定义3.4
(1) $f(x)$在 $x_0$的某个右(左)半去心邻域有定义，如果存在实数 $A$，对任意的 $\varepsilon>0$，存在 $\delta>0$，对任意的 $x\in(x_0,x_0+\delta)(x\in(x_0-\delta,x_0))$，都有 $|f(x)-A|<\varepsilon$，则称 $f(x)$在 $x_0$处的左(右)极限存在，记为 $\lim_{x\to {x_0}^{+}}{f(x)}=A(\lim_{x\to {x_0}^{-}}{f(x)}=A)$ (2) $f(x)$在 $x_0$的某个右(左)半去心邻域有定义，如果对任意的正数 $M>0$，存在正数 $\delta>0$，对任意的 $x\in(x_0,x_0+\delta)(x\in(x_0-\delta,x_0))$，都有 $f(x)>M$，则称 $f(x)$是 $x\to {x_0}^{+}(x\to {x_0}^{-})$过程的正无穷大量，记为 $\lim_{x\to {x_0}^{+}}{f(x)}=+\infty(\lim_{x\to {x_0}^{-}}{f(x)}=+\infty)$(3) $f(x)$在 $x_0$的某个右(左)半去心邻域有定义，如果对任意的正数 $M>0$，存在正数 $\delta>0$，对任意的 $x\in(x_0,x_0+\delta)(x\in(x_0-\delta,x_0))$，都有 $f(x)<-M$，则称 $f(x)$是 $x\to {x_0}^{+}(x\to {x_0}^{-})$过程的正无穷大量，记为 $\lim_{x\to {x_0}^{+}}{f(x)}=-\infty(\lim_{x\to {x_0}^{-}}{f(x)}=-\infty)$

对左右极限，前面的定理都是成立的，形式也是类似的，这里就不一一列出
实际上，左右极限是逼近某个点的两个方向，那么，如果在某个点的极限存在，那么理所应当地，无论以何种方式逼近这个点，极限都应当是相同的，就有如下定理：
定理3.3 $f(x)$在 $x_0$处极限等于 $A$的充分必要条件是 $f(x)$在 $x_0$处的左右极限都等于 $A$

证明是容易的，这里省略

函数极限也有相应地单调收敛定理，证明和数列极限是类似的，我们这里仅列出，证明过程省略
定理3.4
(1)如果存在 $\delta>0$, $f(x)$在 $(x_0,x_0+\delta)$上单调上升(单调下降)并且有下界(有上界)，则 $f(x)$在 $x_0$出的右极限存在
(2)如果存在 $\delta>0$, $f(x)$在 $(x_0-\delta,x_0)$上单调上升(单调下降)并且有上界(有下界)，则 $f(x)$在 $x_0$出的左极限存在
(3)如果 $f(x)$在实轴上单调上升有上界，则 $\lim_{x\to +\infty}{f(x)}$存在
(4)如果 $f(x)$在实轴上单调上升有下界，则 $\lim_{x\to -\infty}{f(x)}$存在

函数极限与数列极限的关系

前面谈到：函数在某个过程的极限存在，那么，无论以何种路径实现该过程 ，都应当只有唯一的极限，这一个路径在实轴上就体现为点列。
定理3.5 A为有限实数或正负无穷
(1) $f(x)$在 $x_0$处的右极限为 $A$的充分必要条件是:对任意的点列 $\{x_n\}$， $x_n > x_0$， $\lim_{n\to \infty}{x_n}=x_0$，都有 $\lim_{n\to\infty}{f(x_n)}=A$(2) $f(x)$在 $x_0$处的左极限为 $A$的充分必要条件是:对任意的点列 $\{x_n\}$， $x_n < x_0$， $\lim_{n\to \infty}{x_n}=x_0$，都有 $\lim_{n\to\infty}{f(x_n)}=A$(3) $f(x)$在 $x_0$处的极限为 $A$的充分必要条件是:对任意的点列 $\{x_n\}$， $x_n \neq x_0$， $\lim_{n\to \infty}{x_n}=x_0$，都有 $\lim_{n\to\infty}{f(x_n)}=A$(4) $\lim_{x\to +\infty}{f(x)}=A$的充分必要条件是：对任意的点列 $\{x_n\}$， $\lim_{n\to \infty}{x_n}=+\infty$，都有 $\lim_{n\to\infty}{f(x_n)}=A$(5) $\lim_{x\to -\infty}{f(x)}=A$的充分必要条件是：对任意的点列 $\{x_n\}$， $\lim_{n\to \infty}{x_n}=-\infty$，都有 $\lim_{n\to\infty}{f(x_n)}=A$

证：
我们仅以有限实数为例证明(1)，其他证明是相当类似的。
必要性，如果 $\lim_{x\to {x_0}^{+}}{f(x)}=A$，则任意的 $\varepsilon>0$，存在 $\delta>0$，当 $0<x-x_0<\delta$时，有 $|f(x)-A|<\varepsilon$对任意的点列 $\{x_n\}$， $x_n \neq x_0$， $\lim_{n\to \infty}{x_n}=x_0$，存在 $N$， $n\ge N$时，有 $|x_n-x_0|<\delta$，从而 $|f(x_n)-f(x_0)|<\varepsilon$充分性，如果对任意的点列 $\{x_n\}$， $x_n < x_0$， $\lim_{n\to \infty}{x_n}=x_0$，都有 $\lim_{n\to\infty}{f(x_n)}=A$反证法证明，如果 $\lim_{x\to {x_0}^{+}}{f(x)} \neq A$，那么存在正数 $\varepsilon_0>0$，对任意 $n\ge 1$，存在 $x_0<x_n<x_0+\frac{1}{n}$，并且： $|f(x_n)-A|\ge {\varepsilon_0}$而 $\lim_{n\to\infty}{x_n}=x_0$，矛盾

定理3.5提供了一种判断极限不存在的方法，也就是取一个数列，证明这个数列的极限不存在，就可以证明函数的极限不存在。

连续情形下的柯西收敛原理

连续情形下也有柯西收敛原理，只不过在连续情形下，极限过程有5种，相应的柯西收敛原理也有5种，我们一一列举出来，并证明右极限情形，其他极限过程的柯西收敛原理原理是类似的。
定理3.6（连续情形下的柯西收敛定理）
(1) $\lim_{x\to{x_0}^{+}}{f(x)}$存在的充分必要条件是：对任意的 $\varepsilon>0$，存在 $\delta>0$，对任意的 $x_1,x_2\in (x_0,x_0+\delta)$，都有 $|f(x_1)-f(x_2)|<\varepsilon$(2) $\lim_{x\to{x_0}^{-}}{f(x)}$存在的充分必要条件是：对任意的 $\varepsilon>0$，存在 $\delta>0$，对任意的 $x_1,x_2\in (x_0-\delta,x_0)$，都有 $|f(x_1)-f(x_2)|<\varepsilon$(3) $\lim_{x\to{x_0}}{f(x)}$存在的充分必要条件是：对任意的 $\varepsilon>0$，存在 $\delta>0$，对任意的 $x_1,x_2 \in (x_0-\delta,x_0)\cup(x_0,x_0+\delta)$，都有 $|f(x_1)-f(x_2)|<\varepsilon$(4) $\lim_{x\to{+\infty}}{f(x)}$存在的充分必要条件是：对任意的 $\varepsilon>0$，存在 $M>0$，对任意的 $x_1,x_2\ge M$，都有 $|f(x_1)-f(x_2)|<\varepsilon$(5) $\lim_{x\to{-\infty}}{f(x)}$存在的充分必要条件是：对任意的 $\varepsilon>0$，存在 $M>0$，对任意的 $x_1,x_2\le -M$，都有 $|f(x_1)-f(x_2)|<\varepsilon$

证：
仅证明(1)，其他证明类似
必要性是显然的，仅证明充分性：
任取一个点列 $\{x_n=x_0+\frac{1}{n}\}$，那么显然， $\{f(x_n)\}$是柯西列。
由数列极限的柯西收敛原理， $\{f(x_n)\}$收敛，令 $\lim_{n\to\infty}{f(x_n)}=A$
下面证明： $\lim_{x\to{x_0}^{+}}{f(x)}=A$
考察估计式： $|f(x)-A|\le |f(x)-f(x_n)| + |f(x_n)-A|$对任意的 $\varepsilon>0$，存在 $\delta>0$，对任意的 $x_1,x_2\in (x_0,x_0+\delta)$，都有 $|f(x_1)-f(x_2)|<\frac{\varepsilon}{2}$存在正整数 $n$，满足， $\frac{1}{n}<\delta$，同时， $|f(x_n)-A|<\frac{\varepsilon}{2}$
当 $0<x-x_0<\delta$时，都有 $|f(x)-A|\le |f(x)-f(x_n)| + |f(x_n)-A|<\varepsilon$

函数的连续性

连续性与间断点

定义3.5 $f(x)$在 $x_0$的某个邻域上有定义，如果 $\lim_{x\to x_0}{f(x)}=f(x_0)$，则称 $f(x)$在 $x_0$点处连续，如果 $f(x)$在区间 $I$上每个点都连续，那么称 $f(x)$在 $I$上连续

按左右极限的关系，有
定义3.6
$f(x)$在 $x_0$的右(左)半邻域上有定义，如果 $\lim_{x\to {x_0}^{+}}{f(x)}=f(x_0)(\lim_{x\to {x_0}^{-}}{f(x)}=f(x_0))$，则称 $f(x)$在 $x_0$点处右(左)连续

有如下定理
定理3.7 $f(x)$在 $x_0$上连续的充要条件是 $f(x)$在 $x_0$上左连续且右连续

如果 $f(x)$在 $x_0$上不连续，称 $x_0$是 $f(x)$的间断点，那么间断的情况有哪几种呢？
按照定理3.7，连续需要左右极限都存在，并且都等于 $f(x_0)$
第一种情况：如果左右极限都存在，但至少有一个不等于 $f(x_0)$，此时， $f(x)$在 $x_0$处是跳跃的
第二种情况：如果左右极限其中之一不存在，但是是广义收敛的，那么此时我们就称 $x_0$是无穷间断点
第三种情况：左右极限其中之一不存在，并且不是广义收敛的，那么 $f(x)$在 $x_0$的一侧像三角函数一样上下波动，但是波动幅度不会缩小

定义3.7
(1) $f(x)$在 $x_0$处左右极限存在，但不全等于 $f(x_0)$，则称 $x_0$是 $f(x)$的第一类间断点
(2) $f(x)$在 $x_0$处左右极限存在且相等，但不等于 $f(x_0)$，则称 $x_0$是 $f(x)$的可去间断点
(3) $f(x)$在 $x_0$处左右极限存在但不相等，则称 $x_0$是 $f(x)$的跳跃间断点
(4) $f(x)$在 $x_0$处左右极限至少有其一不存在，则称 $x_0$是 $f(x)$的第二类间断点
(5) $f(x)$在 $x_0$处有， $\lim_{x\to {x_0}^{+}}=\pm \infty$或 $\lim_{x\to {x_0}^{-}}=\pm \infty$，
则称 $f(x)$是无穷间断点

由极限的四则运算法则，连续函数也对四则运算封闭
定理3.8
(1) $f(x)$和 $g(x)$在 $x_0$上连续，则 $f(x)\pm g(x)$在 $x_0$上连续
(2) $f(x)$和 $g(x)$在 $x_0$上连续，则 $f(x)g(x)$在 $x_0$上连续
(3) $f(x)$和 $g(x)$在 $x_0$上连续, $g(x_0)\neq 0$，则 $\frac{f(x)}{g(x)}$在 $x_0$上连续

另外，连续函数还对复合函数和反函数运算封闭
定理3.9
$g(y)$在 $y=y_0$处连续， $y_0=f(x_0)$， $f(x)$在 $x=x_0$处连续，则 $g(f(x))$在 $x=x_0$处连续

证：
对任意的 $\varepsilon>0$，存在 $\delta_1>0$， $|y-y_0|<\delta_1$时,有 $|g(y)-g(y_0)|<\varepsilon$又存在 $\delta_2>0$， $|x-x_0|<\delta_2$时，有 $|f(x)-f(x_0)|<\delta_1$此时，有 $|g(f(x))-g(f(x_0))|<\varepsilon$

实际上，定理3.9还有更弱的形式：
定理3.10 $g(y)$在 $y=y_0$处连续， $\lim_{x\to {x_0}^{+}}{f(x)}=y_0 (\lim_{x\to {x_0}^{-}}{f(x)}=y_0)$，则 $\lim_{x\to {x_0}^{+}}{g(f(x))}=g(y_0) (\lim_{x\to {x_0}^{-}}{g(f(x))}=g(y_0))$

证明是类似的，这里我们就不给出具体的证明
为了讨论连续函数的反函数性质，我们首先要明确，反函数存在的条件，我们在证明了闭区间上连续函数的性质之后，我们将证明闭区间 $[a,b]$上连续函数反函数存在的条件是 $f(x)$在 $[a,b]$上严格单调，下面的证明用到一个事实： $[a,b]$上连续函数的值域都是闭区间，我们先承认这个事实，在下一节进行证明。
定理3.11 $f(x)$是 $[a,b]$上严格单调上升(下降)的连续函数，则 $f^{-1}(y)$是 $[f(a),f(b)]$上严格单调上升(下降)的连续函数

证：
仅证明单调上升的情形
首先证明 $f^{-1}$是严格单调上升的，对任意的 ${f(a)}\le{y_1}<y_2\le{f(b)}$，令 $x_1=f^{-1}(y_1)$， $x_2=f^{-1}(y_2)$
按照反函数的定义， $y_1=f(x_1),y_2=f(x_2)$
如果 $x_1\ge{x_2}$，由 $f$的单调性，应有 $y_1=f(x_1)\ge f(x_2) = y_2$，与 $y_1<y_2$矛盾。
其次证明 $f^{-1}$的连续性，由单调性，对任意的 $y\in[f(a),f(b)]$， $f^{-1}$在 $y$处的左右极限都是存在的（如果在端点则只有左极限或右极限）
我们证明右极限情形，左极限是类似的
对任意的 $\varepsilon>0$，不妨设 $f^{-1}(y)+\varepsilon<b$，就有 $y<f(f^{-1}(y)+\varepsilon)$对任意的 $y<y^{\prime}<f(f^{-1}(y)+\varepsilon)$，由严格单调性，有 $f^{-1}(y)<f^{-1}(y^{\prime})<f^{-1}(y)+\varepsilon$
这就证明了： $\lim_{y^{\prime}\to y }{f^{-1}(y^{\prime})}=f^{-1}(y)$

闭区间上连续函数的性质

下面我们讨论闭区间上连续函数的性质
定理3.12（有界性定理和最值定理） $f(x)$是闭区间 $[a,b]$上的连续函数，则 $f(x)$在闭区间 $[a,b]$上有界，并且上下界可以取到

证：
(1)先证有界性：如果 $f(x)$在 $[a,b]$上无界，那么可以取得 $[a,b]$的一个数列 $\{x_n\}$， $\lim_{n\to \infty}{|f(x_n)|}=+\infty$，由魏尔斯特拉斯定理， $\{x_n\}$存在收敛子列 $\{x_{n_k}\}$， $\lim_{k\to\infty}{x_{n_k}}=x_0$，则 $\lim_{k\to \infty}{|x_{n_k}|}=+\infty$，而由连续性，应当有 $\lim_{k\to \infty}{|x_{n_k}|}=f(x_0)$，矛盾
(2)再证明上下确界可以取到：记 $M=\sup\{f(x):x\in[a,b]\}$，取 $[a,b]$的一个数列 $\{x_n\}$，满足： $M\ge{f(x_n)}>M-\frac{1}{n}$，再由魏尔斯特拉斯定理，取 $\{x_n\}$的收敛子列 $\{x_{n_k}\}$，有 $M\ge{f(x_{n_k})}>M-\frac{1}{n_k}$两边对 $k\to \infty$取极限，再由夹逼准则，有 $\lim_{k\to\infty}{f(x_{n_k})}=M$而设 $\lim_{k\to\infty}{x_{n_k}}=x_0$，又有 $\lim_{k\to\infty}{f(x_{n_k})}=f(x_0)=M$下确界情形的证明是类似的

定理3.13 $f(x)$是闭区间 $[a,b]$上的连续函数， $M,m$为 $f(x)$在闭区间 $[a,b]$的最大值和最小值，对任意的 $m\le{y}\le{M}$，存在 $x\in[a,b]$，使得 $y=f(x)$

证：
如果 $f(a)=y$，那么结论自然成立，在假设 $y<M$，否则结论显然成立
不失一般性，设 $f(a)<y$，而 $f(a)>y$的证明是类似的。
令 $S=\{t\in[a,b]:\forall x \in[a,t],f(x)<y\}$，首先 $S$是非空并且由上界的，同时， $b\notin S$
令 $t_0=\sup(S)$，这意味着，对任意的 $a<t<t_0$，都有 $f(t)<y$，那么，由函数极限的不等式性质，应当有 $f(t_0)\le {y}$。
但是，按照 $S$的构造，又不能有 $f(t_0)<y$，假设 $f(t_0)<y$
首先， $t_0<b$，否则对任意的 $x\in[a,b]$，都有 $f(x)\le y$，与 $M$是最大值矛盾
其次，由 $f(t_0)<y$，就可以取得 $t_0$的一个右半邻域，在这个右半邻域上都有 $f(x)<y$，这又与 $t_0=\sup(S)$矛盾
综上， $f(t_0)=y$

综合定理3.12及定理3.13，就可以得到如下推论
推论3.1 闭区间上连续函数的值域是闭区间

接下来，我们给出一个更强的连续性，对于连续函数来说，对任意的 $\varepsilon>0$，都存在 $\delta>0$， $|x-x_0|<\delta$时，有 $|f(x)-f(x_0)|<\varepsilon$
但给定 $\varepsilon$， $\delta$是和 $x_0$有关的，可以认为 $\delta$是 $x_0$的函数
然而，很多时候，我们需要这个 $\delta$和点的选取无关，而闭区间上的连续函可以做到这一点
定义3.8
$f(x)$是定义在区间 $I$上的函数，如果对任意的 $\varepsilon>0$,存在正数 $\delta>0$，对任意的 $x_1\in I,x_2\in I,|x_1-x_2|<\delta$，都有 $|f(x_1)-f(x_2)|<\varepsilon$则称 $f(x)$在区间 $I$上一致连续

定理3.14 $f(x)$是闭区间 $[a,b]$上的连续函数，则 $f(x)$在闭区间 $[a,b]$上一致连续

证：
用反证法证明。
假设 $f(x)$在闭区间 $[a,b]$上不一致连续，则存在正数 $\varepsilon_0>0$，可以取到 $[a,b]$中的两个点列 $\{x_n\}$和 $\{y_n\}$，满足 $|x_n-y_n|<\frac{1}{n}$，但 $|f(x_n)-f(y_n)|\ge{\varepsilon_0}$取子列使得 $\{x_{n_k}\}$和 $\{y_{n_k}\}$都收敛，则 $\lim_{k\to\infty}{x_{n_k}}=\lim_{k\to\infty}{y_{n_k}}=x_0$有 $|f(x_{n_k})-f(y_{n_k})|\ge{\varepsilon_0}$两边对 $k\to\infty$取极限，由连续性，有 $|f(x_0)-f(x_0)|\ge{\varepsilon_0}$矛盾

初等函数的连续性

接下来，我们来证明初等函数的连续性，只要证明了基本初等函数的连续性，那么再由连续函数的四则运算及复合函数法则，对基本初等函数进行有限次四则运算及复合函数运算，得到的都是连续函数，这样就证明了全体初等函数都是连续。我们再日常遇到的大多都是初等函数，这就说明了连续函数就足以满足我们许多需求。

三角函数的连续性

对任意的 $\Delta x$，对任意的 $x$，由两角和的公式，有 $\sin{(x+\Delta x)}-\sin{x}\\ =\sin{x}\cos{\Delta x}+\cos{x}\sin{\Delta x}-\sin{x}\\ =\sin{x}(\cos{\Delta x}-1)+\cos{x}\sin{\Delta x}\\ =2\sin{x}(\sin{\frac{\Delta x}{2}})^2+ \cos{x}\sin{\Delta x}$对上式进行放缩 $0\le|\sin{(x+\Delta x)}-\sin{x}|\\ \le 2|(\sin{\frac{\Delta x}{2}})^2|+|\sin{\Delta x}|\\ \le \frac{{\Delta x}^2}{2} + |{\Delta x}|$应用夹逼准则，就有 $\lim_{\Delta x\to 0}{|\sin{(x+\Delta x)}-\sin{x}|}=0$这就证明了 $\sin{x}$在整个数轴上都是连续的

对任意的 $\Delta x$，对任意的 $x$，由两角和的公式，有 $\cos{(x+\Delta x)}-\cos{x}\\ =\cos{x}\cos{\Delta x}-\sin{x}\sin{\Delta x}-\cos{x}\\ =\cos{x}(\cos{\Delta x}-\cos{x})-\sin{x}\sin{\Delta x}\\ =2\cos{x}(\sin{\frac{\Delta x}{2}})^2-\sin{x}\sin{\Delta x}$当然，由以上等式的形式，再沿用上面的证明方法，就可以知道， $\cos{x}$在整个数轴上都是连续的
全体三角函数都可以由 $\sin{x}$和 $\cos{x}$通过四则运算表出，因此，全体三角函数都是连续的，再由反函数的连续法则，反三角函数也是连续函数

指数函数与对数函数

对 $a>0$，我们首先要给出 $a^b(b\in R)$的定义。因为我们再初等数学中，只学过 $b$为有理数情形下的定义
我们先来回顾指数是有理数情形该如何定义？首先，当 $b$是正整数时，就定义为 $b$个 $a$相乘。
当 $b=\frac{1}{n}$，就定义为实数 $c\ge 0$，满足： $c^n=a$，实际上，这样的实数可以通过二分法找到，首先，找一个完全平方数 $N^2>a$，令 $I_0=[0,N^2]$
令 $I_0=[a_0,b_0]$，考察区间的中点 $c_0$，如果 $c_0^n=a$就找到满足条件的 $c$，否则，如果 $c_0^n<a$，令 $I_1=[c_0,b_0]=[a_1,b_1]$，如果 $c_0^n>a$，令 $I_1=[a_0,c_0]=[a_1,b_1]$
考察区间 $I_1$的中点 $c_1$，如果 $c_1^n=a$就找到满足条件的 $c$，否则，如果 $c_1^n<a$，令 $I_2=[c_1,b_1]=[a_2,b_2]$，如果 $c_1^n>a$，令 $I_2=[a_1,c_1]=[a_2,b_2]$
依此类推 $\cdots$
如果以上步骤能在有限步内结束，那么就找到了 $a^b$，否则，就得到一个闭区间套 $\{I_n\}$，由闭区间套定理，存在唯一的 $c\in \bigcap_{n=1}^{\infty}{I_n}$
只要验证其满足 $c^n=a$，实际上，函数 $f(x)=x^n$是连续函数
这是因为 $f(x+\Delta x)-f(x) \\=\sum_{k=0}^{n}{C_n^k x^{n-k}{\Delta x}^k}-x^n \\=\sum_{k=1}^{n}{C_n^k x^{n-k}{\Delta x}^k}$ $x^k$在 $0$处连续
事实上， $x^k$在 $(0,+\infty)$上的严格单调上升的，并且有下界0，有单调有界收敛原理， $x^k$在 $0$处的右极限存在，而 $0 < \frac{1}{n^k} <\frac{1}{n}$再由夹逼准则，有 $\lim_{n\to\infty}{(\frac{1}{n})^k}=0$由函数极限与数列极限的关系， $x^k$在 $0$点连续
因此， $x^n$在整个实轴上连续
按照构造，有 $b_k\to c$，并且， $b_k^n>a$，再由构造 $a_k \to c$，并且， $a_k^n<a$，由极限的不等式性质， $c^n\ge a$，同时 $c^n\le a$，于是， $c^n=a$
再由 $x^n$的严格单调性， $c$是一意的
对正有理数 $q=\frac{m}{n}$，并且 $m,n$互素， $a^q$就定义为 $a^q=(a^m)^{\frac{1}{n}}$
对负有理数 $q$， $a^q$定义为 $\frac{1}{a^{-q}}$
对互质的两个正整数 $m,n$，有 $a^{\frac{m}{n}}=(a^{\frac{1}{n}})^m$实际上，如果 $c=a^{\frac{1}{n}}$，那么： $(c^m)^n=(c^n)^m=a^m$这样， $c^m= (a^{\frac{1}{n}})^m = (a^m)^{\frac{1}{n}}=a^{\frac{m}{n}}$
从而， $a^{-\frac{m}{n}}=(a^{\frac{1}{n}})^{-m}$
我们再验证：对任意的正整数 $k$， $a^{\frac{1}{kn}}=(a^{\frac{1}{n}})^{\frac{1}{k}}$
令 $c=a^{\frac{1}{kn}}$， $d=c^k$，则 $d^n=(c^k)^n=c^{kn}=a$因此， $d=a^{\frac{1}{n}}$， $c=d^{\frac{1}{k}}$
这样，有 $a^{\frac{m}{n}}=(a^{\frac{1}{n}})^m=((a^{\frac{1}{kn}})^k)^m=(a^{\frac{1}{kn}})^{km}$ $a^{-\frac{m}{n}}=(a^{\frac{1}{n}})^{-m}=((a^{\frac{1}{kn}})^k)^{-m}=(a^{\frac{1}{kn}})^{-km}$下面证明：以上定义的指数幂有如下性质：
(1)对任意的两个有理数 $r,s$，对任意正实数 $a$，都有 $a^{r+s}=a^r a^s$(2)对任意的两个有理数 $r,s$，对任意正实数 $a>1$， $r<s$，有 $a^r<a^s$

证：
(1)设 $r=\frac{m}{n}$, $s=\frac{k}{t}$，其中， $s,t$是正整数， $m,n$
是整数。\
有
$a^r=(a^{\frac{1}{nt}})^{mt}$
$a^s=(a^{\frac{1}{nt}})^{kn}$
$r+s=\frac{mt+kn}{nt}$，故
$a^{r+s}=(a^{\frac{1}{nt}})^{mt+kn}$
$a^r a^s = (a^{\frac{1}{nt}})^{mt} (a^{\frac{1}{nt}})^{kn} = (a^{\frac{1}{nt}})^{mt+kn}$
因此， $a^{r+s}=a^r a^s$
(2) $a^s = a^r a^{s-r}$，容易验证， $a^{s-r}>1$，因此 $a^s > a^r$

对实数 $r$，对实数 $a>1$，定义： $a^r = \inf\{a^q:q\in Q,q> r\}$，这样，对实数 $r$, $a^r$都是有意义的。容易验证，当 $r$是有理数时，两个定义都是相等的。下面我们验证：对任意两个实数 $r,s$，都有 $a^{r+s}=a^r a^s$成立

证：
首先，对任意的 $c>1$，取有理数 $q_1>r,q_2>s$，满足：
$a^{q_1}<c a^r$
$a^{q_2}<c a^s$
有
$a^{r+s}\le a^{q_1+q_2} =a^{q_1} a^{q_2} < c^2 a^r a^s$
由 $c$的任意性，得到
$a^{r+s} \le a^r a^s$
在证明反向不等式：
对任意的 $c>1$，取有理数 $q>r+s$，取有理数 $q_1>r$, $q_2>s$，
同时， $q=q_1+q_2$。\
有 $c a^{r+s} > a^{q} = a^{q_1} a^{q_2} \ge a^r a^s$
由 $c$的任意性，就可证得反向不等式

对 $a>1$，对任意的实数 $x$，及增量 $\Delta x$，有： $\frac{a^{x+\Delta x}}{a^{x}} = a^{\Delta x}$由以上等式，可以得到 $f(x)=a^x$在整个实轴是严格单调上升的，因为：当 $\Delta x>0$时，任取有理数 $q>\Delta x$，再取有理数 $0<q_2<\Delta x$，一定有 $1<a^{q_2}<a^q$对任意的 $c>1$，不妨取 $a^q<c a^{\Delta x}$，于是 $1<a^{q_2}<c a^{\Delta x}$由 $c$的任意性，得到 $1<a^{q_2}\le a^{\Delta x}$当 $\Delta x>0$时，必有 $\frac{a^{x+\Delta x}}{a^{x}} >1$再证明 $f(x)=a^x(a>1)$在整个实轴上是连续的 $a^{x+\Delta x}-a^{x}=a^x(a^{\Delta x}-1)$只要验证 $f(x)$在 $x=0$处连续即可。
下面我们证明以下极限： $\lim_{n\to\infty}{a^{\frac{1}{n}}}=1(a>1)$

证：
首先， $a^{\frac{1}{n}}>1$\
其次，由均值不等式， $a^{\frac{1}{n}} \le \frac{a-1+n}{n}$
再由夹逼准则可以证得结论

于是
$\lim_{n\to\infty}{a^{-\frac{1}{n}}}= \lim_{n\to\infty}{\frac{1}{a^{\frac{1}{n}}}}=1$由单调收敛原理， $f(x)$在 $0$处左右极限都存在。再由两个极限，有 $\lim_{x\to 0^{+}}{a^x}=\lim_{x\to 0^{-}}{a^x}=1=a^0$这样就证得了 $f(x)$在整个实轴上严格单调上升且连续

对 $0<a<1$， $a^x$定义为 $\frac{1}{(\frac{1}{a})^x}$，此时， $f(x)=a^x$在整个实轴上单调下降且连续
对数函数定义为指数函数的反函数，记为 $\log_a{y}$，按照定义，有 $a^{\log_a{y}}=y(y>0)$因此， $a^{\log_a{y_1}}a^{\log_a{y_2}}=a^{\log_a{y_1}+\log_a{y_2}}=y_1 y_2$从而对数函数有如下性质： $log_a{y_1 y_2}=log_a{y_1}+log_a{y_2}$有当 $0<a<1$时，对数函数在 $(0,+\infty)$上单调下降且连续
有当 $a>1$时，对数函数在 $(0,+\infty)$上单调上升且连续

幂函数

首先，容易验证：在 $p,q$都是有理数， $a>1$情况下，有 $a^{pq}=(a^p)^q$再由指数函数的连续性，对任意的实数 $r,s$， $a>1$，都有 $a^{rs}=(a^r)^s$当 $x>0$，对任意的 $\alpha$，都有： $x^\alpha = e^{\alpha \ln{x}}$由复合函数的连续性法则： $f(x)=x^\alpha$就在 $(0,+\infty)$上连续。
但当 $x\le 0$时， $x^\alpha$不一定有意义，因此，要特别注意幂函数的定义域。
我们仅对指数时有理数情况进行讨论：当 $\alpha = \frac{m}{n}$，其中 $m,n$互质,当 $n$是奇数时才有意义，此时， $x<0$时， $x^\alpha = (-1)^m (-x)^\alpha$
由复合函数连续性，幂函数也在定义域内连续。综合以上全部论述，有：
定理3.15 初等函数在其定义域内是连续的

常用的等价无穷小

例3.2 $x\to 0$时 $\sin{x} \sim x \sim \tan{x} \sim \arcsin{x} \sim \arctan{x}$

证：
(i) $\sin{x}\sim\tan{x}$ $\lim_{x\to 0}{\frac{\sin{x}}{\tan{x}}}=\lim_{x\to 0}{\cos{x}}=1$
(ii) $x\sim\arcsin{x}$ $\lim_{t\to 0}{\frac{t}{\arcsin{t}}}=\lim_{t\to 0}{\frac{\sin{(\arcsin{t})}}{\arcsin{t}}}$注意到 $\lim_{t\to 0}{\arcsin{t}}=\arcsin{0}=0$ $g(x)= \begin{cases} 1 & x=0\\ \frac{\sin{x}}{x} & x\neq 0 \end{cases}$ $g(x)$在 $x=0$处连续， $f(t)=arcsin{t}$在 $t=0$处连续，因此 $\lim_{t\to 0}{\frac{t}{\arcsin{t}}}=g(f(0))=1$(iii)同理可证 $\arctan{x}\sim x$

例3.3 $x\to 0$时 $e^x - 1 \sim x \sim \ln{(x+1)}$

证：
考察函数 $f(x)=(1+x)^{\frac{1}{x}}(x\in(-1,0)\cup(0,+\infty))$， $x>0$时 $(1+x)^{[\frac{1}{x}]} \le (1+x)^{\frac{1}{x}} \le (1+x)^{[\frac{1}{x}]+1}$ $(1+x)^{[\frac{1}{x}]} \ge (1+\frac{1}{1+[\frac{1}{x}]})^{[\frac{1}{x}]}$ $(1+x)^{[\frac{1}{x}]+1} \le (1+\frac{1}{[\frac{1}{x}]})^{[\frac{1}{x}]+1}$而： $\lim_{x\to 0^{+}}{(1+\frac{1}{1+[\frac{1}{x}]})^{[\frac{1}{x}]}} =\lim_{n\to\infty}{(1+\frac{1}{1+n})^n}=e$ $\lim_{x\to 0^{+}}{(1+\frac{1}{[\frac{1}{x}]})^{[\frac{1}{x}]+1}} =\lim_{n\to\infty}{(1+\frac{1}{n})^{n+1}}=e$由夹逼准则： $\lim_{x\to 0^{+}}{(1+x)^{\frac{1}{x}}}=e$当 $0<x<1$时，有估计式： $f(x)=\frac{1}{(1+x)^{-\frac{1}{x}}}=\frac{1}{(1-\frac{1}{-\frac{1}{x}})^{-\frac{1}{x}}}$ $(1-\frac{1}{-\frac{1}{x}})^{-\frac{1}{x}} \le (1-\frac{1}{1+[-\frac{1}{x}]})^{[-\frac{1}{x}]}$ $\lim_{x\to 0^{-}}{(1-\frac{1}{1+[-\frac{1}{x}]})^{[-\frac{1}{x}]}} =\lim_{n\to\infty}{(1-\frac{1}{n+1})^n} =\lim_{n\to\infty}{\frac{1}{(1+\frac{1}{n})^n}} =\frac{1}{e}$ $(1-\frac{1}{-\frac{1}{x}})^{-\frac{1}{x}} \ge (1-\frac{1}{[-\frac{1}{x}]})^{[-\frac{1}{x}]+1}$ $\lim_{x\to 0^{-}}{(1-\frac{1}{[-\frac{1}{x}]})^{[-\frac{1}{x}]+1}} =\lim_{n\to\infty}{(1-\frac{1}{n})^{n+1}} =\lim_{n\to\infty}{(1-\frac{1}{n})^2\frac{1}{(1+\frac{1}{n-1})^{n-1}}} =\frac{1}{e}$由夹逼准则： $\lim_{x\to 0^{-}}{(1+x)^{\frac{1}{x}}}=e$在 $x=0$处补充定义 $e$，即： $f(x)= \begin{cases} e & x=0\\ (1+x)^{\frac{1}{x}} & x \in (-1,0)\cup (0,+\infty) \end{cases}$ $f(x)$在 $x=0$处连续。 $\lim_{x\to 0}{\frac{\ln{(1+x)}}{x}} =\lim_{x\to 0}{\ln{(1+x)^{\frac{1}{x}}}} =\lim_{x\to 0}{\ln{f(x)}} =\ln(f(0))=1$ $\begin{aligned} \lim_{x\to 0}{\frac{e^x-1}{x}} =\lim_{x\to 0}{\frac{e^x-1}{\ln{(e^x-1+1)}}} =\lim_{t\to 0}{\frac{t}{\ln{(t+1)}}} =1 \end{aligned}$

例3.4 $x\to 0$时 $1-\cos{x} \sim \frac{1}{2} x^2$

证：
$\begin{aligned} \lim_{x\to 0}{ \frac{1-\cos{x}}{\frac{1}{2} x^2} } =\lim_{x\to 0}{ \frac{2(1-\cos{x})}{x^2} }= \lim_{x\to 0}{ \frac{4(\sin{\frac{x}{2}})^2}{x^2} } =\lim_{x\to 0}{(\frac{\sin{\frac{x}{2}}}{\frac{x}{2}})^2}=1 \end{aligned}$

例3.5 $x\to 0$时，对任意的 $\alpha$，都有 $(1+x)^{\alpha} -1 \sim \alpha x$

证：
实际上，有 $\lim_{x\to 0} \frac{(1+x)^{\alpha}-1}{\alpha x} = \lim_{x\to 0}\frac{e^{\alpha \ln{(1+x)}}-1}{\alpha x}=\lim_{x\to 0}\frac{\alpha \ln{(1+x)}}{\alpha x} = 1$