虽然学习了机器学习的一些算法,其中涉及的数学知识虽然也能看明白,但是为了加强记忆与理解以及提高对机器学习的认识,特又跟着老师们一起具体学习一下相关的数学知识,当然了刚考完研或者数学专业的孩子对下面的数学知识还是可以略过的。
首先了解什么是机器学习
对于某给定的 任务T,在合理的性能度量方案P的前提下,某计算机程序可以自主学习 任务T的经验E,随着提供合适、优质、大量的 经验 E,该程序对于任务T的性能逐步提高。
这里最重要的是机器学习的对象:
1.任务 Task,T,一个或者多个
2.经验 Experience,E
3.性能 Performance,P
即:随着任务的不断执行,经验的累积会带来计算机性能的提升。
换个表述什么是机器学习
机器学习是人工智能的一个分支。我们使用计算机设计一个系统 ,使它能够根据提供的训练数据按照一定的方式来学习;随着训练次数的增加,该系统可以在性能上不断学习和改进;通过参数优化的学习模型,能够用于预测相关问题的输出。
机器学习的内涵与外延
机器学习可以解决什么
给定数据的预测问题:数据清洗/特征选择、确定算法模型、参数优化、结果预测
不能解决什么
大数据存储 并行计算、做一个机器人
机器学习的建模过程:
1.给出训练数据与对应标签,训练的数据包括文本、声音、图像、交易等。
2.进行数据的清洗/特征选择
3.选择适当的机器学习算法,对数据开始训练,并在验证集上进行验证
4.得出对应的回归或分类模型
5.给出全新的一组数据括文本、声音、图像、交易等,使用模型进行预测或分类。
机器学习的一般流程概括的表示:数据收集→数据清洗→特征工程→数据建模
下面是相关的数学知识点的介绍,这里有三次课,所以分了三次笔记:
首先来看一个例子:求S的值
![]()
问题分析:
令:![]() ,对f(x)求导
,对f(x)求导
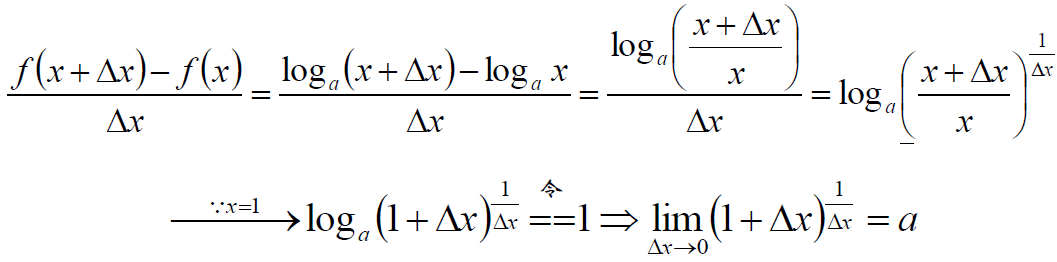
可以作出这样疑问:
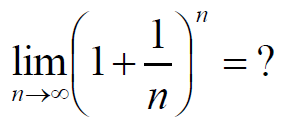
构造数列{xn}

所以:![]() 有上界,因此,必有极限,记做e。
有上界,因此,必有极限,记做e。
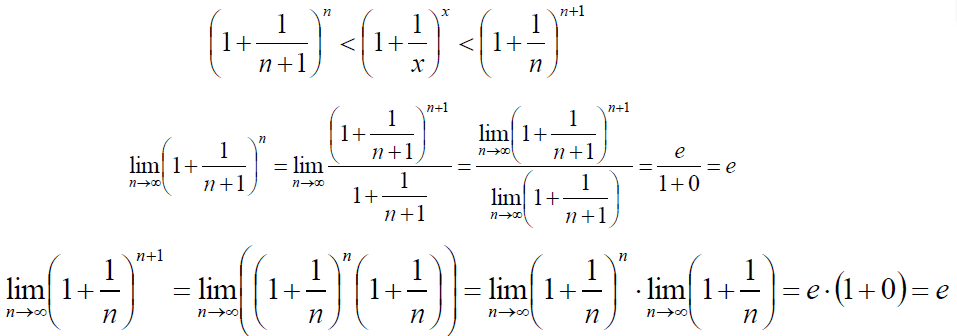
根据两边夹定理,函数![]() 的极限存在,为e。
的极限存在,为e。
导数在机器学习中尤为常见
简单的说,导数就是曲线的斜率,是曲线变化快慢的反应
二阶导数是斜率变化快慢的反应,表征曲线凸凹性
二阶导数连续的曲线,往往称之为“光顺”的。
还记得高中物理老师时常念叨的吗:加速度的方向总是指向轨迹曲线凹的一侧。
根据![]() 可以得到函数f(x)=lnx的导数,进一步根据换底公式、反函数求导等,得到其他初等函数的导数。
可以得到函数f(x)=lnx的导数,进一步根据换底公式、反函数求导等,得到其他初等函数的导数。
常用函数的导数
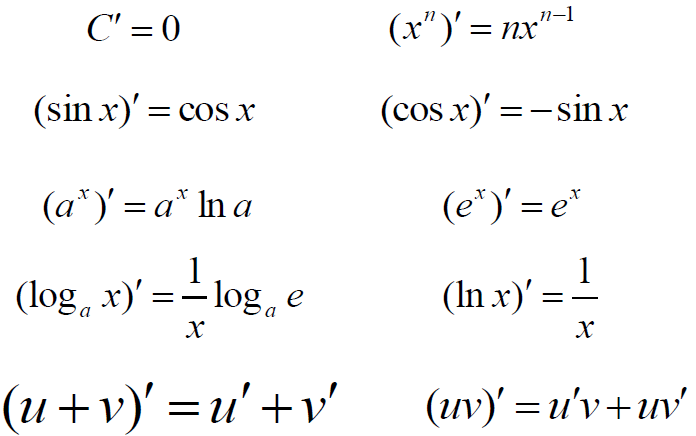
导数应用
已知函数f(x)=xx,x>0,求f(x)的最小值
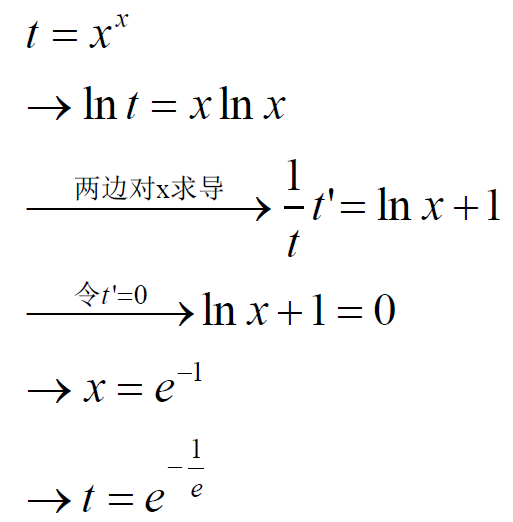
幂指函数的求导,是先要将其转化为对数形式这样比较方便,或者直接转化为以e指数形式。
积分应用N→∞→lnN!→N(lnN-1)

Taylor公式– Maclaurin公式
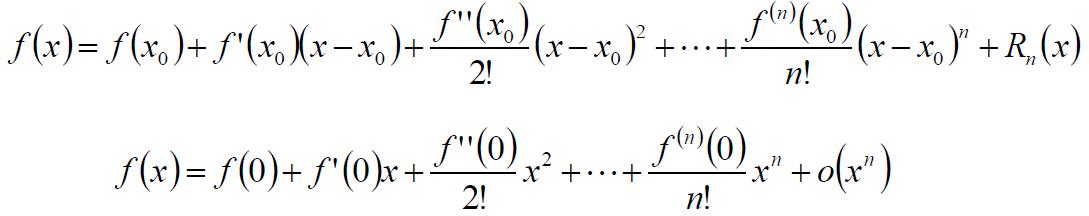
Taylor公式的应用1
数值计算:初等函数值的计算(在原点展开)

Taylor公式的应用2
考察Gini系数的图像、熵、分类误差率三者之间的关系
将f(x)=-lnx在x=1处一阶展开,忽略高阶无穷小,得到f(x)≈1-x
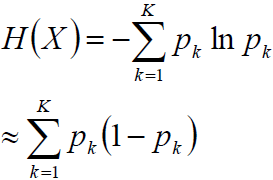

上述结论,在决策树章节中会进一步讨论
方向导数
如果函数 z=f(x,y) 在点 P(x,y) 是可微分的,那么,函数在该点沿任一方向 L 的方向导数都存在,且有: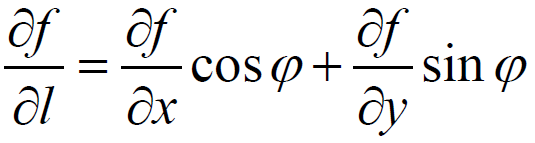
其中, ψ 为 x 轴到方向 L 的转角。
梯度
设函数 z=f(x,y) 在平面区域 D 内具有一阶连续偏导数,则对于每一个点 P(x,y)∈D ,向量
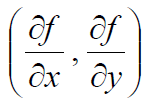
为函数z=f(x,y) 在点 P 的梯度,记做 grad f(x,y)
梯度的方向是函数在该点变化最快的方向
考虑一座解析式为 z=H(x,y) 的山,在 (x0, y0)的梯度是在该点坡度变化最快的方向。
Γ函数
![]()
Γ函数是阶乘在实数上的推广:
![]()
凸函数
若函数 f 的定义域 domf 为凸集,且满足
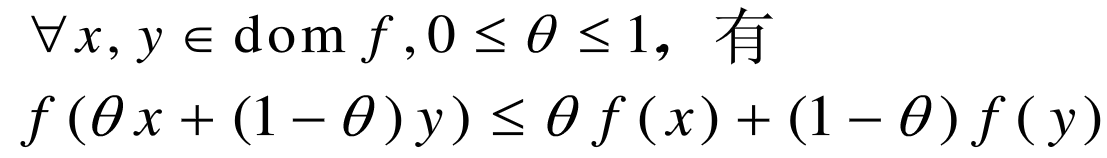
一阶可微
若 f 一阶可微,则函数 f 为凸函数当前仅当 f 的定义域 domf 为凸集,且
![]()

二阶可微
若函数 f 二阶可微,则函数 f 为凸函数当前仅当 dom 为凸集,且
![]()
若 f 是一元函数,上式表示二阶导大于等于 0
若 f 是多元函数,上式表示二阶导 Hessian 矩阵半正定。
凸函数举例:

概率论
对概率的认识: P(x)∈[0,1]
P=0 事件出现的概率为 0,但不一定不发生
若 x 为离散连续变量,则 P(x=x0) 表示 x0发生的概率/概率密度
累计分布函数: Φ(x)=P(x≤x0)
Φ(x) 一定为 单增函数
min(Φ(x))=0 ,max(Φ(x))=1
思考:将值域为 [ 的某单增函数 y=F(x) 看成 X 事件的累积概率函数
若 y=F(x) 可导,则 f(x)=F’(x) 为某概率密度函数
古典概型
举例:将 n 个不同的球放入 N(N≥n) 个盒子中,假设盒子容量无限,求事件 A={ 每个盒子至多有 1 个球 }的概率。
解:
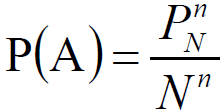
基本事件总数:
第1个球,有N种放法;
第2个球,有N种放法;
……
共:Nn种放法。
每个盒子至多放1个球的事件数:
第1个球,有N种放法;
第2个球,有N-1种放法;
第3个球,有N-2种放法;
……
共:![]()
组合数背后的秘密N→∞→lnN!→N(lnN-1)
