
定积分的定义与性质
定积分的定义
定积分的概念来源于求和运算的连续化,我们目前已知的求和手段都是有限求和,为了将求和运算扩充到无限个数求和,必须引入极限手段。扩充手段有两种——可列情形对应的是级数理论,不可列情形对应的则是积分。但我们都要首先清楚,本节所讨论的本质,就是无穷情形下的“求和”运算。
定义7.1
f(x)是定义在闭区间
[a,b]的函数,
x0,x1,⋯,xn满足:
a=x0<x1<⋯<xn=b,集合
{x0,x1,⋯,xn}称为
[a,b]的一个分划,记为
Δ
对每个小区间:
[xi−1,xi](i=1,⋯,n),取
ξi∈[xi−1,xi](i=1,⋯,n),和式:
∑i=1nf(ξi)(xi−xi−1)称为
f(x)在分划
Δ下的一个Riemann和,记为
S(Δ,f)
Riemann和有鲜明的几何意义,见下图,为了求得曲线
y=f(x)在
[a,b]区间上的曲线段下的面积,我们通常用有限矩体进行逼近。Riemann和的每一项对应一个矩形的面积,可以预见:当区间越分越细的时候,矩形面积和就逼近图形的真实面积,就是定积分的基本思想。
定义7.2
f(x)是定义在闭区间
[a,b]的函数,
Δ={x0,x1,⋯,xn}是
[a,b]的任意分划,令
λ(Δ)=max1≤i≤n(xi−xi−1),如果存在实数
I,对任意的
ε>0,存在
δ>0,当
λ(Δ)<δ时,无论小区间内点如何选取,都有
∣S(Δ,f)−A∣<ε则称
f(x)在闭区间
[a,b]上Riemann可积,简称可积,
I称为
f(x)在闭区间
[a,b]上的积分,记为
∫abf(x)dx=I
定积分的几何意义就是区间
y=f(x)与
x轴,连同
x=a,
x=b围成图形的面积。
定积分的可积性理论——达布理论
下一个问题是:满足什么条件下,
f(x)在闭区间
[a,b]是可积的?我们先从连续函数入手。
定理7.1 闭区间
[a,b]上的连续函数都是Riemann可积的
证:
为了证明闭区间
[a,b]上的连续函数
f(x)都是Riemann可积的,我们首先要找到一个实数
I,也就是
f(x)的积分值,其次,再证明
f(x)的积分就是
I。
第一步:找一个实数
I。
先取一个分划列
Δn={x0(n),x1(n),⋯,x2n(n)},其中
xk(n)=a+2nk(b−a),令区间
Ik(n)=[xk−1(n),xk(n)],
k=1,⋯,2n,
n=1,2,⋯。那么
Δn是
Δn−1的加细(即
Δn⊂Δn−1),再令
Mk(n)=maxx∈Ik(n)(f(x)),
mk(n)=minx∈Ik(n)(f(x)),作和式
S(Δn)=k=0∑2nMk(n)2nb−a
S(Δn)=k=0∑2nmk(n)2nb−a则
S(Δn)是单调下降的,
S(Δn)是单调上升。令
I=limn→∞S(Δn),
I=limn→∞S(Δn)
S(Δn)−S(Δn)=2nb−ak=0∑(Mk(n)−mk(n))由
f(x)在
[a,b]上连续,
f(x)在
[a,b]上一致连续,对任意的
ε>0,存在
δ>0,对任意的
[a,b]内两点
x1,x2
,只要
∣x1−x2∣<δ,就有
∣f(x1)−f(x2)∣<b−aε再由连续性
f(x)在
[a,b]上可取得最大值和最小值。这样,只要
2nb−a<δ就有
(Mk(n)−mk(n))<b−aε
S(Δn)−S(Δn)<ε记
I=I=I
第二步,证明:
∫abf(x)dx=I
对任意的分划
Δ,令
Δn′=Δn∪Δ,再令
Δn′={y0(n),y1(n),⋯,ykn(n)},其中
a=y0(n)<y1(n)<⋯<ykn(n)=b,任取一个Riemann和
S(Δ,f),设
ξk(n)是区间
[yk−1(n),yk(n)]在
Δ中对应的分划中,
f(x)的取点。
Mk′′(n),mk′(n)是
f(x)在区间
[yk−1(n),yk(n)]的最大值和最小值。
同时令
S(Δn′)=i=0∑knMk′(n)(yk(n)−yk−1(n))
S(Δn′)=i=0∑knmk′(n)(yk(n)−yk−1(n))由于
Δn′是
Δn的加细,就有
S(Δn)≤S(Δn′)≤S(Δn′)≤S(Δn)由夹逼准则,就有
n→∞limS(Δn′)=n→∞limS(Δn′)=I对任意的
ε>0,存在
N,
n≥N时,有
∣n→∞limS(Δn′)−I∣<2ε取定一个
n,又由一致连续性,存在
δ>0,当
∣x1−x2∣<δ时,
∣f(x1)−f(x2)<2(b−a)ε,这样,当
λ(Δ)<δ时,
∣ξk(n)−Mk′(n)∣<2(b−a)ε,于是
∣S(Δ,f)−S(Δn′)∣<2ε
∣S(Δ,f)−I∣≤∣S(Δ,f)−S(Δn′)∣+∣ξk(n)−Mk′(n)∣<ε
从正面过程可以知道,一致连续性对可积性来说是十分重要的一个性质。
对一般的函数,在每个小区间上不一定能取到最大值和最小值。然而,我们依然可以仿照以上证明过程,给出一个上和和下和的概念。
定义7.3
f(x)是闭区间
[a,b]的一个有界函数,
Δ={x0,x1,⋯,xn}是
[a,b]的一个分划,
a=x0<x1<⋯<xn=b,
Mi=supxi−1<x<xif(x),mi=infxi−1<x<xif(x),称和式
S(Δ,f)=∑i=0nMi(xi−xi−1)是
f在
[a,b]上的达布上和,
S(Δ,f)=∑i=0nmi(xi−xi−1)是
f在
[a,b]上的达布下和
容易证明如下三条引理
引理7.1
f(x)是闭区间
[a,b]的一个有界函数,
Δ={x0,x1,⋯,xn}是
[a,b]的一个分划,
a=x0<x1<⋯<xn=b,
S(Δ,f)是一切
f在
Δ上的Riemann和的上确界,
S(Δ,f)是一切
f在
Δ上的Riemann和的下确界
引理7.2
f(x)是闭区间
[a,b]的一个有界函数,
Δ1,Δ2是
[a,b]的两个分划,并且,
Δ1⊂Δ2,则
S(Δ1)≤S(Δ2)≤S(Δ2)≤S(Δ1)
引理7.3
f(x)是闭区间
[a,b]的一个有界函数,则
f(x)的任意达布下和不超过任意达布上和,即使他们对应不同的分划
这样,一切达布上和有下界,一切达布上和有上界,那么达布上和有下确界,我们记为
I,达布下和有上确界,我们记为
I,并且
I≤I。类似于连续函数可积性的证明过程,我们猜想:
I=I=I时,
I就是
f(x)在
[a,b]上的积分。
定理7.2 有界函数
f(x)在
[a,b]上可积的充要条件是:
λ(Δ)→0lim[S(Δ,f)−S(Δ,f)]=0
证:
必要性,如果
f(x)在
[a,b]上可积,设
I=∫abf(x)dx。
对任意的
ε>0,存在
δ>0,对任意的分划
Δ,当
λ(Δ)<δ时,任意
S(Δ,f)都有:
I−ε<S(Δ,f)<I+ε由引理7.2
S(Δ,f)≤I+ε
S(Δ,f)≥I−ε就有
I−ε≤S(Δ,f)≤I≤I≤S(Δ,f)≤I+ε这样,
S(Δ,f)−S(Δ,f)≤2ε这就说明了,
λ(Δ)→0lim[S(Δ,f)−S(Δ,f)]=0同时,由
ε的任意性,还可以得出
I=I的结论
充分性,如果
λ(Δ)→0lim[S(Δ,f)−S(Δ,f)]=0由不等式:
S(Δ,f)≤I≤I≤S(Δ,f)≤可以得出结论:
I=I
设
I=I=I,对任意的分划
Δ,就有
S(Δ,f)≤I≤S(Δ,f)对任意的Riemann和,都有
S(Δ,f)≤S(Δ,f)≤S(Δ,f)这样,
0<∣S(Δ,f)−I∣≤S(Δ,f)−S(Δ,f)对任意的
ε>0,存在
δ>0,
λ(Δ)<δ时,都有
S(Δ,f)−S(Δ,f)<ε这样,任意的
S(Δ,f)都有
∣S(Δ,f)−I∣<ε这就证明了
∫abf(x)dx=I
从证明的过程也可以看出,如果可积时,一定有
I=I=∫abf(x)dx但上下积分相等能不能直接得到可积性呢?实际上,我们由如下的达布定理。
定理7.3(达布定理)
f(x)是闭区间
[a,b]上的有界函数,则有
λ(Δ)→0limS(Δ)=I
λ(Δ)→0limS(Δ)=I
由达布定理,就有如下推论:
推论7.1
f(x)是
[a,b]上的有界函数,则
f(x)在
[a,b]上Riemann可积的充要条件是
I=I
下面我们证明定理7.3:
证: 我们仅证
limλ(Δ)→0S(Δ)=I,
limλ(Δ)→0S(Δ)=I的证明是类似的。
对任意
ε>0,取由上积分的定义,存在分划列
{Δ0},满足
I≤S(Δ0,f)<I+2ε对任意的分划
Δ,令
Δ0′=Δ0∪Δ,就有
I≤S(Δ0′,f)≤S(Δ0,f)<I+2ε只要考察
∣S(Δ,f)−S(Δ0′,f)∣即可
实际上,对
Δ的每一个小区间,如果其中没有
Δn的分点,
Δ和
Δn′对应的项没有差距,差别就体现在插入了
Δn分点的小区间上。
不妨设
∣f(x)∣≤M>0,如果某个小区间插入了一个分点,那么对应的上确界之差不超过
2M,设
N为
Δn的分点个数(
N>2)。那么,如果
Δ的某个区间完全含在
Δ0的某个区间内,那么,
Δ0′内的某个区间与
Δ的这个区间是相同的,不会对达布上和有影响,对达布上和有影响的只有插入了
Δ0分点的区间,最多只有
N−2个
Δ的区间对达布上和影响,假设
Δ的某个区间
[xk−1,xk]中插入了一个分点
c(c∈(xk−1,xk)),设
f(x)在
[xk−1,c]上的上确界为
M1,在
[c,xk]上上确界为
M2,在
[xk−1,xk]的上确界为
M0,从而
≤∣M1(c−xk−1)+M2(xk−c)−M0(xk−xk−1)∣≤2M(xk−xk−1)2Mλ(Δ)从而
∣S(Δ,f)−S(Δ0′,f)∣≤2M(N−2)λ(Δ)当
λ(Δ)<4M(N−2)ε时
≤∣S(Δ,f)−I∣∣S(Δ,f)−S(Δ0′,f)∣+∣S(Δ0′,f)−I∣<ε因此
λ(Δ)→0limS(Δ,f)=I
可积函数类
定积分的性质
下面,我们来证明定积分的一些性质。
定理7.4(有界性)
f(x)在
[a,b]上可积,那么
f(x)就在
[a,b]上有界。
证:
设
∫abf(x)dx=I,反证法证明,如果
f(x)无界,那么任取分划
Δ:a=x0<x1<⋯<xn=b,必然有一个小区间无界,设就是
[x0,x1]
可以取得
ξn∈[x0,x1],使得
∣f(ξn)∣>n,这样,无论
λ(Δ)有多小,都可以取得
ξn∈[x0,x1],在其他区间的取法给定的条件下,Riemann和可以任意大,与可积矛盾
因此,对积分的讨论都是建立在有界函数上的。下面我们还要证明如下的定理。
定理7.5
f(x)在
[a,b]上可积,则
∣f(x)∣在
[a,b]上可积
证:
这是因为对任意的
x1,x2∈[a,b],都有
∣∣f(x1)∣−∣f(x2)∣∣≤∣f(x1)−f(x2)∣对任意的分划
Δ:a=x0<x1<⋯<xn=n,
0≤S(Δ,∣f∣)−S(Δ,∣f∣)≤S(Δ,f)−S(Δ,f)令
λ(Δ)→0,就有
λ(Δ)→0limS(Δ,∣f∣)−S(Δ,∣f∣)=0
类似地,可以证明:
定理7.6
f(x)在
[a,b]上可积,则
f(x)在
[a,b]的任意子区间可积
证明比较简单,这里就不写出具体的证明过程了。
下面,我们就可以给出Riemann积分的一些性质。
定理7.7
(1)(线性性质)
f(x)和
g(x)在
[a,b]上Riemann可积,则对任意的实数
c,d,
cf(x)+dg(x)在
[a,b]上Riemann可积,并且
∫abcf(x)+dg(x)dx=c∫abf(x)dx+d∫abg(x)dx(2)(不等式性质)
f(x)和
g(x)在
[a,b]上Riemann可积,并且
f(x)≤g(x),∀x∈[a,b],则
∫abf(x)dx≤∫abg(x)dx(3)(绝对值性质)
f(x)在
[a,b]上Riemann可积,则
∣∫abf(x)dx∣≤∫ab∣f(x)∣dx(4)(区间可加性)对任意的
a<c<b,
f(x)在
[a,b]上可积的充要条件是
f(x)在
[a,c]和
[c,b]上都可积,并且
∫acf(x)dx+∫cbf(x)dx=∫abf(x)dx
证:
(1)对任意的分划
Δ:a=x0<x1<⋯,xn=b,对任意的
ξk∈[xk−1,xk](k=1,⋯,n),有
∣k=1∑n[cf(ξn)+dg(ξn)(xk−xk−1)]−c∫abf(x)dx−d∫abg(x)dx∣≤∣c∣∣k=1∑nf(ξn)(xk−xk−1)−∫abf(x)dx∣+∣d∣∣k=1∑ng(ξn)(xk−xk−1)−∫abg(x)dx∣对任意的
ε>0,存在
δ1>0,
λ(Δ)<δ1时,有
∣k=1∑nf(ξn)(xk−xk−1)−∫abf(x)dx∣<2∣c∣ε又存在
δ2>0,
λ(Δ)<δ2时,有
∣k=1∑ng(ξn)(xk−xk−1)−∫abg(x)dx∣<2∣d∣ε因此,当
λ(Δ)<min(δ1,δ2)时,就有
∣k=1∑n[cf(ξn)+dg(ξn)(xk−xk−1)]−c∫abf(x)dx−d∫abg(x)dx∣<ε(2)(3)的证明比较简单,省略
下面证明(4):只证明前一个命题,后一个命题比较容易,而前一命题只需要证明充分性
实际上,由达布定理,我们只需要取得一个分划列
{Δn},
λ(Δn)→0,有
S(Δn)−S(Δn)→0就可以证得可积性,而这可以通过分别取
[a,c]和
[c,b]的分划列
{Δn1}和
{Δn2},再合并成
{Δn}即可证得结论。
微积分基本定理
微积分基本定理
上一章,我们把微分的逆运算称为“不定积分”,但从定积分的定义来看,“不定积分”离真正的“积分”的定义还相去甚远。本节要证明的微积分基本定理,正是搭起微分和积分的一座桥梁。
定理7.8(微积分基本定理)
f(x)在
[a,b]上可积且原函数存在,原函数为
F(x),则
∫abf(x)dx=F(b)−F(a)
证:对
[a,b]的任意分划
Δ:a=x0<x1<⋯<xn=b,有
F(b)−F(a)=k=1∑nF(xk)−F(xk−1)(1)由拉格朗日中值定理,存在
ξk∈(xk−1,xk),满足
F(xk)−F(xk−1)=f(ξk)(xk−xk−1)
k=1,⋯,n,代入(1)中,有
F(b)−F(a)=k=1∑nf(ξk)(xk−xk−1)再令
λ(Δ)→0,按照定积分的定义,有
∫abf(x)dx=F(b)−F(a)
微积分基本定理将原函数和积分联系在一起,而原函数是微分的逆运算,因此,在原函数存在的情况下,就为定积分的计算提供了一种手段。
变上限积分的性质
微积分基本定理要求
f(x)可积,可积性问题由达布理论可以解决。还要求
f(x)原函数存在,原函数存在性问题,我们至今没有介绍,现在,我们利用定积分,可以回答这个问题。
定理7.9
(1)
f(x)在
[a,b]上可积,那么变上限积分
∫axf(x)dx是
[a,b]上的连续函数
(2)如果
f(x)在
[a,b]上连续,那么变上限积分
∫axf(x)dx在
[a,b]上可导,并且导函数为
f(x)
利用定理7.9的结论(2),就有如下推论:
定理7.10(原函数存在定理) 闭区间上的连续函数都存在原函数
在证明定理7.9之前,我们先证明积分第一中值定理:
定理7.11(积分第一中值定理)
f(x)在
[a,b]上连续,可积函数
g(x)在
[a,b]非负,则存在
ξ∈[a,b],使得
∫abf(x)g(x)dx=f(ξ)∫abg(x)dx
证:
设
f(x)在
[a,b]上的最大值和最小值分别为
M和
m,由积分的不等式性质,有
m∫abg(x)dx≤∫abf(x)g(x)dx≤M∫abg(x)dx不妨设
∫abg(x)dx>0,从而
m≤∫abg(x)dx∫abf(x)g(x)dx≤M再由连续函数的介值定理,存在
ξ∈[a,b],满足:
f(ξ)=∫abg(x)dx∫abf(x)g(x)dx
下面我们证明定理7.9:
证:(1)
∣∫ax+Δxf(x)dx−∫axf(x)dx∣≤∣∫xx+Δxf(x)dx∣≤∫xx+Δx∣f(x)∣dx由
f(x)可积,
f(x)有界,设
∣f(x)∣≤M>0,则
∣∫ax+Δxf(x)dx−∫axf(x)dx∣≤M∣Δx∣对任意的
ε>0,当
∣Δx∣<Mε时,就有
∣∫ax+Δxf(x)dx−∫axf(x)dx∣<ε(2)
Δx→0limΔx∫xx+Δxf(x)dx=Δx→0limΔxf(ξ)Δx=Δx→0limf(ξ)=f(x)以上等式中的
ξ介于
x和
x+Δx之间
定积分的换元积分法和分部积分法
由微积分基本定理,我们就可以把求原函数的换元积分法和分部积分法,推广到定积分的计算当中。
定理7.12
ϕ(t)在
[a,b]上可导,
f(ϕ(t))ϕ′(t)在
[a,b]上可积,
f(x)在
[ϕ(a),ϕ(b)]上可积且原函数存在,则
∫abf(ϕ(t))ϕ′(t)dt=∫ϕ(a)ϕ(b)f(x)dx
证:
由于
f(x)在
[ϕ(a),ϕ(b)]上的原函数存在,设为
F(x)
F(ϕ(t))是
f(ϕ(t))ϕ′(t)在
[a,b]的原函数。
由微积分基本定理,有
∫abf(ϕ(t))ϕ′(t)dt=F(ϕ(b))−F(ϕ(a))
∫ϕ(a)ϕ(b)f(x)dx=F(ϕ(b))−F(ϕ(a))因此,
∫abf(ϕ(t))ϕ′(t)dt=∫ϕ(a)ϕ(b)f(x)dx
定理7.13 如果
x=ϕ(t)的导数恒为正,
f(x)在
[a,b]上可积,
f(ϕ(t))ϕ′(t)在
[ϕ−1(a),ϕ−1(b)]上存在原函数且可积,则
∫abf(x)dx=∫ϕ−1(a)ϕ−1(b)f(ϕ(t))ϕ′(t)dt
定理7.14
f(x),g(x)可导,
g(x)原函数为
G(x),
f′(x)G(x)在
[a,b]上的原函数存在且可积,则
∫abf(x)g(x)dx=f(b)G(b)−f(a)G(a)−∫abf′(x)G(x)dx
证明是类似的,这里不证。
积分第二中值定理
积分第二中值定理在反常积分的证明中十分关键,我们先给出积分第二中值定理的内容。
定理7.15(积分第二中值定理)
g(x)在
[a,b]上可积
(1)
f(x)在
[a,b]上单调上升,
f(x)≥0,则存在
ξ∈[a,b]
∫abf(x)g(x)dx=f(b)∫ξbg(x)dx(2)
f(x)在
[a,b]上单调下降,
f(x)≥0,则存在
ξ∈[a,b]
∫abf(x)g(x)dx=f(a)∫aξg(x)dx(3)
f(x)在
[a,b]上单调,则存在
ξ∈[a,b]
∫abf(x)g(x)dx=f(a)∫aξg(x)dx+f(b)∫ξbg(x)dx
由于定理的条件十分宽松,因此,我们不妨把条件加强给出一个简单的证明,再从这个证明中寻找证明的思路。
假设
f(x)在
[a,b]上单调上升且有连续导数,
g(x)在
[a,b]连续,令
G(x)=∫xbg(t)dt,
G′(x)=−g(x),由分部积分法:
∫abf(x)g(x)dx=−∫abf(x)dG(x)=−f(x)G(x)∣ab+∫abf′(x)G(x)dx=f(a)∫abg(t)dt+∫abf′(x)G(x)dx(3)设
M,m是
G(x)在
[a,b]上的最大值和最小值,那么就有
m∫abf′(x)dx≤∫abf′(x)G(x)dxM∫abf′(x)dx即
m≤f(b)−f(a)∫abf′(x)G(x)dx≤M再由连续函数的介值定理,存在
ξ∈[a,b]
G(ξ)=f(b)−f(a)∫abf′(x)G(x)dx
再代入到(3)中,就可以得到
∫abf(x)g(x)dx=f(a)∫aξg(x)dx+f(b)∫ξbg(x)dx
虽然
g(x)不一定连续,但是只要
g(x)可积,函数
G(x)=∫axg(t)dt就是连续的,不妨设
f(x)单调下降且非负,并且设
f(a)>0,只要我们证明了
m≤f(a)∫abf(x)g(x)dx≤M在利用连续函数的介值定理,就能证得结论(2),只要证得结论(2)
∫abf(x)g(x)dx=∫ab[f(x)−f(a)]g(x)dx+f(a)∫abg(x)dx再套用结论(2),就能证得结论(3)的单调下降情形,也就是说,我们只需要证明结论(1)和(2),就能证得结论(3)。
在一般的条件下,我们不能用分部积分法,只能借助定积分的定义进行证明,在证明之前,我们先给出阿贝尔变换。
引理7.4(阿贝尔变换)
a1,⋯,an和
b1,⋯,bn是实数,
Bk=∑i=1kbk,则
k=1∑nakbk=anBn+k=1∑n−1(ak−ak+1)Bk
下面我们用阿贝尔变换来证明结论(2)
证:
设
f(x)单调下降且
f(b)≥0,对任意的
[a,b]的分划
Δ,其中
Δ:a=x0<x1<⋯<xn=b,则
∫abf(t)g(t)dt=λ(Δ)→0limk=0∑n∫xk−1xkf(t)g(t)dt设
∣g(x)∣≤M>0
∣k=1∑n∫xk−1xkf(t)g(t)dt−k=1∑nf(xk−1)∫xk−1xkg(t)dt∣≤k=1∑n∫xk−1xk∣f(t)−f(xk−1)∣∣g(t)∣dt≤Mk=1∑nwk(xk−xk−1)当
λ(Δ)→0时,
∣k=1∑n∫xk−1xkf(t)g(t)dt−k=1∑nf(xk−1)∫xk−1xkg(t)dt∣→0因此,就有
∫abf(t)g(t)dt=λ(Δ)→0limk=1∑nf(xk−1)∫xk−1xkg(t)dt由阿贝尔变换:
k=1∑nf(xk−1)∫xk−1xkg(t)dt=k=1∑n−1[f(xk−1)−f(xk)]∫axkg(t)dt+f(xn−1)∫abg(t)dt设
G(x)=∫axg(t)dt,设
M,m是
G(x)的最大值和最小值,就有
f(a)m=m[f(xn−1)+k=1∑n−1(f(xk−1)−f(xk))]≤k=1∑nf(xk−1)∫xk−1xkg(t)dt≤Mf(a)因此,有
f(a)m≤∫abf(x)g(x)dx≤f(a)M
再利用介值定理就可以证得结论
定积分的几何应用
平面图形的面积
我们知道定积分的几何意义是曲边梯形的面积,由此我们可以得到计算平面图形面积的方法。我们先引入最简单的两种情形——X型区域和Y型区域。所谓X型区域,即由两条曲线
y=f(x),y=g(x),x∈[a,b]以及两条直线
x=a,x=b围成的区域,其中
f(x)≥g(x),x∈[a,b],如下图所示:

由定积分的几何意义,阴影部分的面积为以
y=f(x)为顶边的曲边梯形的面积减去以
y=g(x)为顶边的曲边梯形的面积。于是,该X型区域的面积为
∫ab[f(x)−g(x)]dx。同样地可以给出Y型区域以及其面积的求法。这是比较简单的情形,我们常常遇到的是由某一个曲线围成的图形,而曲线常常由参数方程
γ:{x=x(t)y=y(t)其中
t∈[α,β],并且
x(α)=x(β),y(α)=y(β),除了起点和终点外没有重合的点。我们再规定
x(t),y(t)连续可导,即有连续的导数。这种情形下,围成的图形的面积应该如何计算呢?我们先对
γ进行定向,如下图所示

为何规定正定向呢,我们先来看
γ围成一个X型区域的情形

当
t从
α变动到
t1时,
x(t)严格单调上升,存在反函数
t=t−1(x),代入到
y=y(t),得到
y=y(t−1(x))=ϕ(x),这样,由
y=ϕ(x),x∈[x(t1),x(α)]为顶边的曲边梯形的面积为
S1=∫x(t1)x(α)ϕ(x)dx作变换
x=x(t),得到
S1=∫t1αy(t)x′(t)dt=−∫αt1y(t)x′(t)dt同理,当
t从
t1变动到
β时,
x(t)单调上升,其反函数
t=t2−1(x)代入到
y=y(t)中,得到
ϕ2(x)=y(t2−1(x)),以
y=ϕ2(x)为顶边的曲边梯形的面积为
S2=∫x(t1)x(β)ϕ2(t)dt=∫t1βy(t)x′(t)dt从而X型区域的面积为
S=S1−S2=−∫αβy(t)x′(t)dt类似地,如果围成的区域是一个Y型区域,那么,计算公式为
∫αβx(t)y′(t)dt。在上面求解过程中,正定向移动起到面积正负抵消的作用,对于一般的图形,若在某个过程
[t1,t2]中,
x(t)单调下降,那么按照公式,其曲边梯形的面积取正值,若单调下降,按公式,其曲边梯形的面积取负值,运动一周后,正负相抵,恰好得到
γ所围成的图形的面积。我们以下面的图形来说明这一点

令
S(t)=−∫αty(t)x′(t)dt,则随着
t从
α增大到
β,有
S(t1)S(t2)S(t3)S(β)=S1+S2+S3+S4+S5+S6=S1+S2+S6=S1+S2+S6+S3+S4=S1+S4+S6可见,对于一般的曲线围成的区域,其面积计算公式
S=−∫αβy(t)x′(t)dt=∫αβx(t)y′(t)dt=21∫αβ[x(t)y′(t)−y(t)x′(t)]dt简记为
S=21∫γxdy−ydx
例7.1 推导椭圆
a2x2+b2y2=1的面积公式
解:用参数方程表示
{x=acosθy=bsinθ,θ∈[0,2π]椭圆的面积为
S=21∫02π[(acosθ).(bcosθ)−(bsinθ)(−asinθ)]dθ=abπ
微元法
定积分解决的是连续量连续变化的积累或连续作用的总和,这个积累或总和表现出来的是一个量,记为
A。比如在物理学中求解变速直线运动的位移,应当如何做呢?在时间
[0,T]内,速度
v(t)连续变化,为了求解整个过程的位移,我们首先要对
[0,T]进行划分
Δ:0=t0<t1<⋯<tn=T,分别求解
[tk−1,tk]时间段内的位移
Sk
(k=1,2,⋯,n),设总的位移为
S,则
S=k=1∑nSk。只要
λ=1≤i≤nmaxΔtk足够小,
v(t)在
[tk−1,tk]振幅极小(由一致连续性),从而我们将其视为匀速直线运动,任取
ζk∈[tk1,tk],估计
Sk≈v(ζk)Δtk,从而估计
S≈k=1∑nv(ζk)Δtk令
λ→0,这时取精确值
S=∫0Tv(t)dt。为什么可以这么取呢?实际上,有估计式:
mkΔtk≤Sk≤MkΔtk其中
mk和
Mk是
v(t)在
[tk−1,tk]上的最小值和最大值,则
k=1∑nmkΔtk≤S≤k=1∑nMkΔtk而
λ→0时,不等式两边都趋于
∫0Tv(t)dt,这就说明了
S=∫0Tv(t)dt。我们总结一下以上用定积分求解的过程:要考察某个连续量在区间
[a,b]上的累积作用
S,首先要要求这个量是和某个区间相联系的,并且具有区间可加性
第一步:划分区间
a=x0<x1<⋯<xn=b
第二步:假设连续量在区间
[xk−1,xk]上的作用为
Sk,估计
Sk为
Sk=f(ζk)Δxk这其中
f(x)是以连续函数,
ζk∈[xk−1,xk],至于
f(x)如何确定,需要由相应的物理规律或几何知识加以确定,这是最关键的一步
第三步:求和取极限,解得
S=∫abf(x)dx
第二步我们可以写成
dS=f(x)dx,两边积分就有
∫abdS=∫abf(x)dx这很类似于微分的形式,因此我们把这种方法称为微元法,
dS称为微元
极坐标下平面图形的面积
对极坐标下的曲线
r=r(θ)≥0,θ∈[α,β],β−α<2π,求
r=r(θ),θ=α,θ=β围成的图形的面积。我们用微元法来求解:
- 将
[α,β]划分为
α=a0<a1<⋯<an=β,令
S为
r=r(θ),θ=α,θ=β围成的图形的面积,
Sk为
r=r(θ),θ=ak−1,θ=ak围成的图形的面积,
S=k=1∑nSk(k=1,⋯,n)
- 估计
Sk=21r2(ζk)Δθ(k=1,2,⋯,n)
- 加总,求极限,得到
S=21∫αβr2(θ)dθ
如图,上述的第二步实际上就是取某一个半径,以一个扇形取估计
Sk,如下图所示

实际上,设
r(θ)在
[ak−1,ak]上的最小值的最大值分别为
mk,Mk,则
21mk2Δθk≤Sk≤21Mk2Δθk21k=1∑nmk2Δθk≤S≤21k=1∑nMk2Δθk令
λ→0,得到
S=21∫αβr2(θ)dθ
从微元的观点看,
dS=21r2(θ)dθ
例7.2 求心脏线
r=a(1+cosθ),θ∈[0,2π]所围成的面积,其中
a>0
解:
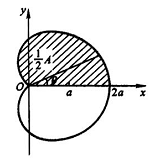
S=2a2∫02π(1+cosθ)2dθ=23a2π
旋转体体积
对于
[a,b]上的连续函数
f(x),曲线
y=f(x),x∈[a,b]绕着
x轴旋转一周,得到的几何体的体积该如何求呢?我们将
[a,b]作分划
Δ:a=x0<x1<⋯<xn=b,设
V为
y=f(x),x∈[a,b]绕着
x轴旋转一周,得到的几何体的体积,
Vk为
y=f(x),x∈[xk−1,xk]绕着
x轴旋转一周
(k=1,⋯,n),按微元法,下面需要对
Vk进行估计,假设在
[xk−1,xk]上
f(x)是常数,得到的几何图形是一个圆柱体,从而
dV=πf2(x)dx,由微元法
V=π∫abf2(x)dx从另一个角度看,设
f(x)在
[xk−1,xk]上的最大值和最小值为
Mk,mk,这样
πmk2Δxk≤Vk≤πMk2Δxkπk=1∑nmk2Δxk≤V≤πk=1∑nMk2Δxk两边令
λ→0,就有
V=π∫abf2(x)dx。类似地,
x=g(y),y∈[a,b]绕着
y轴旋转得到的旋转体的体积应该为
V=π∫abg2(y)dy。
平面曲线的长度
对于一段平面曲线
{x=x(t)y=y(t),t∈[a,b]如何求解其长度呢,求解线段的长度是容易的,因此我们首先想到先将
[a,b]作一个分划
Δ:a=t0<t1<⋯<tn=b,设
[tk−1,tk]段的长度为
sk,
[a,b]段的长度为
s,就有
s=k=1∑nsk,对于
sk,我们采用两端点之间线段的长度来估算
sk≈(x(tk)−x(tk−1))2+(y(tk)−y(tk−1))2
我们设
x(t),y(t)有连续的导数,此时这段曲线是光滑的曲线,由拉格朗日中值定理,存在
ζk,ξk∈[xk−1,xk],满足
x(tk)−x(tk−1)=x′(ζk)Δtk,y(tk)−y(tk−1)=y′(ξk)Δtk,从而
sk≈x′2(ζk)+y′2(ξk)
Δtks≈k=1∑nx′2(ζk)+y′2(ξk)
Δtk由于
x′(t)在
[a,b]上连续,因此一致连续,对任意的
ε>0,存在
δ1>0,当
∣t′−t′′∣<δ1时,
∣f(t′)−f(t′′)∣<2(b−a)ε,当
λ(Δ)<δ时
∣∣∣∣∣k=1∑nx′2(ζk)+y′2(ξk)
Δtk−k=1∑nx′2(ξk)+y′2(ξk)
Δtk∣∣∣∣∣≤k=1∑nx′2(ζk)+y′2(ξk)
+x′2(ξk)+y′2(ξk)
∣x′(ξk)−x′(ζk)∣(∣x′(ξk)∣+∣x′(ζk)∣)Δtk≤k=1∑n∣x′(ξk)−x′(ζk)∣Δtk<2ε因此,我们估计
s≈k=1∑nx′2(ξk)+y′2(ξk)
Δtk存在
δ2>0,当
λ(Δ)<δ2时
∣∣∣∣∣k=1∑nx′2(ξk)+y′2(ξk)
Δtk−∫abx′2(t)+y′2(t)
dt∣∣∣∣∣<2ε从而当
λ(Δ)<min(δ1,δ2)时
∣∣∣∣∣k=1∑nx′2(ζk)+y′2(ξk)
Δtk−∫abx′2(t)+y′2(t)
dt∣∣∣∣∣<ε从而
=λ(Δ)→0limk=1∑n(x(tk)−x(tk−1))2+(y(tk)−y(tk−1))2
∫abx′2(t)+y′2(t)
dt若
y=f(x)在
[a,b]上有连续的导数,其参数方程为
{x=xy=f(x)其弧长为
L=∫ab1+f′2(x)
dx
若是极坐标系表示曲线
r=r(θ),θ∈[α,β],可以改写为参数方程形式
{x=r(θ)cosθy=r(θ)sinθ则弧长为
L=∫αβr′2(θ)+r2(θ)
dθ
这在微元法中,相当于微元为
dS=x′2(t)+y′2(t)
dt,我们称为弧长微元
旋转体的侧面积
下面我们来讨论旋转体侧面积的求解,对曲线
γ:{x=x(t)y=y(t),t∈[a,b]并且
x(t),y(t)都有连续的导数,同时,
x′(t)>0,x∈[a,b],首先,取分划
Δ:a=t0<t1<⋯<tn=b,我们令
Mk(x(tk),y(tk))(k=0,1,⋯,n),利用
M1,M2,⋯,Mn将曲线分隔开若干段。在
[tk−1,tk]段绕
x轴旋转一周所得的旋转体的侧面积为
Sk,整段曲线绕
x轴旋转一周所得的旋转体的侧面积为
S,有
S=k=1∑nSk。下面我们来估算
Sk(k=1,⋯,n)。连接
Mk−1,Mk所得的线段
Mk−1Mk绕
x轴旋转一周的旋转体是一个圆台。圆台的上底面半径为
r1,下底面半径为
r2,母线长为
l,则圆台的侧面积为
π(r1+r2)l,我们就以
Mk−1Mk绕
x轴旋转一周形成的圆台的侧面积作为
Sk的估计,对
k=1,⋯,n,容易写出
Sk的估计为
Sk≈π(y(tk−1)+y(tk))[x(tk)−x(tk−1)]2+[y(tk)−y(tk−1)]2
由介值定理,存在
ξk∈[tk−1,tk],满足
y(ξk)=2y(tk−1)+y(tk),由拉格朗日中值定理,存在
ζk,γk∈[tk−1,tk],满足
x(tk)−x(tk−1)=x′(ζk)Δtky(tk)−y(tk−1)=y′(γk)Δtk则
=π(y(tk−1)+y(tk))[x(tk)−x(tk−1)]2+[y(tk)−y(tk−1)]2
2πy(ξk)x′2(ζk)+y′2(γk)
Δtk设
∣y(t)∣≤M>0,t∈[a,b],再由
x′(t),y′(t)在
[a,b]上连续,故一致连续,对任意的
ε>0,存在
δ1>0,当
∣t′−t′′∣<δ1时,有
∣x′(t′)−x′(t′′)∣<8πM(b−a)ε,∣y′(t′)−y′(t′′)∣<8πM(b−a)ε。则当
λ(Δ)<δ1时
≤≤+<2π∣∣∣∣∣k=1∑ny(ξk)x′2(ζk)+y′2(γk)
Δtk−k=1∑ny(ξk)x′2(ξk)+y′2(ξk)
Δtk∣∣∣∣∣2πk=1∑n∣y(ξk)∣∣∣∣∣∣x′2(ζk)+y′2(γk)
+x′2(ξk)+y′2(ξk)
x′2(ζk)−x′2(ξk)+y′2(γk)−y′2(ξk)∣∣∣∣∣Δtk2Mπk=1∑n[∣x′(ζk)−x′(ξk)∣x′2(ζk)+y′2(γk)
+x′2(ξk)+y′2(ξk)
∣x′(ζk)∣+∣x′(ξk)∣∣y′(γk)−y′(ξk)∣x′2(ζk)+y′2(γk)
+x′2(ξk)+y′2(ξk)
∣y′(γk)∣+∣y′(ξk)∣]Δtk2Mπk=1∑n[4M(b−a)πεΔtk]=2ε再由定积分的定义,存在
δ2>0,当
λ(Δ)<δ2时
2π∣∣∣∣∣k=1∑ny(ξk)x′2(ξk)+y′2(ξk)
Δtk−∫aby(t)x′2(t)+y′2(t)
dt∣∣∣∣∣<2ε当
λ(Δ)<min(δ1,δ2)时
=≤+<π∣k=1∑n(y(tk−1)+y(tk))[x(tk)−x(tk−1)]2+[y(tk)−y(tk−1)]2
−2∫aby(t)x′2(t)+y′2(t)
dt∣2π∣k=1∑ny(ξk)x′2(ζk)+y′2(γk)
Δtk−∫aby(t)x′2(t)+y′2(t)
dt∣2π∣k=1∑ny(ξk)x′2(ζk)+y′2(γk)
Δtk−k=1∑ny(ξk)x′2(ξk)+y′2(ξk)
Δtk∣2π∣k=1∑ny(ξk)x′2(ξk)+y′2(ξk)
Δtk−∫aby(t)x′2(t)+y′2(t)
dt∣2ε+2ε=ε即
=λ(Δ)→0limπk=1∑n(y(tk−1)+y(tk))[x(tk)−x(tk−1)]2+[y(tk)−y(tk−1)]2
2π∫aby(t)x′2(t)+y′2(t)
dt侧面积就为
2π∫aby(t)x′2(t)+y′2(t)
dt,从微元法的角度看,即是
dS=2πy(t)x′2(t)+y′2(t)
dt。利用这个结果,可以得到直角坐标系下旋转体的侧面积为
2π∫aby(x)1+y′2(x)
dx,同理也可以写出极坐标系下的公式,这里就不再赘述了。






