数学分析笔记11：幂级数

幂级数相关概念

幂级数收敛域

幂级数，就是形如 $\sum_{n=1}^{\infty}{a_nx^n}$的函数项级数，其中 $\{a_n\}$是实数列。对幂级数而言，我们收敛要考察幂级数的收敛域，其次，要考察其一致收敛性，再由一致收敛性，就可以得到幂级数的相关性质。首先我们考察幂级数的收敛域。
假设幂级数在 $x=x_0\neq 0$处收敛，那么，对于 $|x|<|x_0|$的点，就有 $\tag{1} a_nx^n=a_nx_0^n(\frac{x}{x_0})^n$由 $\sum_{n=1}^\infty{a_nx_0^n}$收敛，则通项 $\lim_{n\to\infty}{a_nx_0^n}=0$故通项有界，设 $M>0$， $|a_nx_0^n|\le M$，则 $|a_nx^n|\le M |\frac{x_0}{x}|^n$由比较判别法，级数 $\sum_{n=1}^\infty{a_nx^n}$绝对收敛。我们定义： $R=\sup_{r>0}\{\sum_{n=1}^\infty{a_nx^n}在(-r,r)上收敛\}$ $R$称为幂级数 $\sum_{n=1}^\infty{a_nx^n}$的收敛半径，收敛半径就有如下特点：
(1)对任意的 $|x|>R$，幂级数 $\sum_{n=1}^\infty{a_nx^n}$一定发散，这是由 $R$的构造决定的
(2)幂级数在 $(-R,R)$上一定收敛且绝对收敛
(3)对于 $\pm R$两点，幂级数的收敛性，则需要进一步的验证，而不能直接下判断
综合收敛半径和前面数项级数的审敛法，就可以得到幂级数的收敛域，这样，利用幂级数，就得到一类更广阔的函数类。现在，对给定的一个幂级数 $\sum_{n=1}^\infty{a_nx^n}$，如何求其收敛域呢？按照前面的论述在 $(-R,R)$之间，幂级数绝对收敛，在 $(R,+\infty)$及 $(-\infty,R)$上幂级数发散，所以，只要判断幂级数 $\sum_{n=1}^\infty{|a_n|x^n}$的敛散性，确定收敛和发散的临界值，就能得到幂级数的收敛域，这样，正项级数的判别法，就可以用到幂级数收敛半径的判断当中。
按照柯西根值判别法，如果极限 $\lim_{n\to\infty}{\sqrt[n]{|a_n|}}=A$存在，那么， $\lim_{n\to\infty}{\sqrt[n]{|a_n||x|^n}}=A|x|$如果 $A>0$，那么收敛半径自然就是 $\frac{1}{A}$。
如果 $A=+\infty$，那么，只要 $|x|>0$，级数必然发散，那么，收敛半径就是 $0$。
如果 $A=0$，那么，按根值判别法，对任意的 $x$，幂级数都绝对收敛，收敛半径就是 $+\infty$。
无论如何，收敛半径都是 $R=\frac{1}{A}$。
定理11.1 $\{a_n\}$是实数列，如果极限 $\lim_{n\to\infty}{\sqrt[n]{|a_n|}}$为 $A$(实数或无穷)，则
(1) $A=0$，则收敛半径为 $\infty$，即对任意的 $x\in R$，幂级数 $\sum_{n=1}^\infty{a_nx^n}$都收敛。
(2) $0<A<\infty$，则收敛半径为 $\frac{1}{A}$
(3) $A=+\infty$，则收敛半径为0

当然，也可以用达朗贝尔判别法给出幂级数的审敛法，这里就不再详述。

阿贝尔定理

现在我们来讨论幂级数的性质，首先，我们给出幂级数的阿贝尔定理。
定理11.2(阿贝尔定理) 幂级数 $\sum_{n=1}^\infty{a_nx^n}$的收敛半径为 $R$，则
(1)幂级数在 $(-R,R)$任意的闭子区间都绝对一致收敛
(2)如果幂级数在 $x=R$处收敛，则幂级数在 $(0,R]$上一致收敛
(3)如果幂级数在 $x=-R$处收敛，则幂级数在 $[-R,0)$上一致收敛

证：
(1)对任意的 $[-\delta,\delta]$，其中 $\delta<R$，取 $\delta^\prime$，使 $\delta<\delta^\prime<R$。设 $|a_n\delta^{\prime n}|\le M>0$ $|a_nx^n|=|a_n\delta^{\prime n}||\frac{x^n}{\delta^{\prime n}}| \le M(\frac{\delta}{\delta^\prime})^n$由M判别法，幂级数在 $[-\delta,\delta]$上绝对一致收敛。
(2)(3)只证明(2)，(3)的证明是类似的
如果幂级数在 $x=R$处收敛，那么对任意的 $x\in[0,R]$，都有 $a_nx^n=a_nR^n(\frac{x}{R})^n$ 由于 $g(x)=(\frac{x}{R})^n$在 $x\in[0,R]$关于 $n$单调，并且有界，而级数 $\sum_{n=1}^\infty{a_nR^n}$收敛，因此，由阿贝尔判别法，幂级数在 $(0,R]$上一致收敛

由此我们可以得到如下推论。
推论11.1 幂级数在其定义域内一致收敛
既然如此，那么，幂级数一定在其收敛域内是连续函数。
定理11.3 幂级数在收敛域内是连续函数
定理11.4(逐项积分定理) 幂级数 $f(x)=\sum_{n=1}^\infty{a_nx^n}$的收敛半径为 $R$，对任意的 $(-R,R)$内的闭子区间 $[a,b]$， $f(x)$在 $[a,b]$上可积，并且： $\int_a^b{f(x)dx}=\sum_{n=1}^{\infty}{\frac{a_n(b^{n+1}-a^{n+1})}{n+1}}$
那么，幂级数是否可以逐项求导呢？答案是肯定是，但是，我们首先要解决的一个问题的逐项求导之后的幂级数的收敛半径。
引理11.1 幂级数 $f(x)=\sum_{n=1}^\infty{a_nx^n}$的收敛半径为 $R$，则幂级数 $\sum_{n=1}^\infty{na_nx^{n-1}}$的收敛半径也为 $R$

证：
设幂级数 $\sum_{n=1}^\infty{na_nx^{n-1}}$的收敛半径为 $R^\prime$
如果 $\sum_{n=1}^\infty{a_nx^n}$在 $x_0$处收敛，对任意的 $0<x<|x_0|$。
首先，有 $\lim_{n\to\infty}{|a_nx_0^n|}=0$再任取 $x<x^\prime<|x_0|$，就有 $\lim_{n\to\infty}{n|\frac{x}{x^\prime}|^n}=0$因此，存在正数 $M>0$，使得 $n|a_nx_0^n||\frac{x}{x^\prime}|^n \le M$则 $|na_nx_0^n|=|a_nx_0^n|(n|\frac{x}{x^\prime}|^n)|\frac{x^\prime}{x_0}|^n \le M|\frac{x^\prime}{x_0}|^n$由比较判别法，幂级数在 $x$处收敛，因而 $R^\prime \ge R$。
相同的办法可以证明 $R\ge R^\prime$。

定理11.5 幂级数 $f(x)=\sum_{n=1}^\infty{a_nx^n}$的收敛半径为 $R$，则 $f(x)$在 $(-R,R)$上无穷阶可导，并且 $f^{(k)}(x)=\sum_{n=k}^\infty{n(n-1)\cdots(n-k+1)a_nx^{n-k}}$
我们可以看到，幂级数有相当好的性质，就是可以无穷阶逐项可导，无穷阶逐项积分，幂级数的相关计算也是基于此进行了。

解析函数的泰勒展开

泰勒级数

现在，假设我们有一个无穷阶可导的函数 $f(x)$，什么条件下， $f(x)$可以展成幂级数呢？那么，考虑这个问题的第一步，假设 $f(x)$可以展成幂级数，那么系数应该如何确定？
假设 $f(x)=\sum_{n=0}^\infty{a_nx^n}$，当然，这个展开是在收敛域内进行的，那么，在收敛域内， $f(x)$无穷次可导，并且导数等于 $f^{(k)}(x)=\sum_{n=k}^\infty{n(n-1)\cdots(n-k+1)a_nx^{n-k}}$ $f^{(k)}(0)=k!a_k$这说明了 $a_k = \frac{f^{(k)}(0)}{k!}$，这恰好就是Taylor公式的各项系数！因此，如果 $f(x)$无穷阶可导，我们称幂级数： $\sum_{n=0}^\infty{\frac{f^{(n)}(0)}{n!}x^n}$是 $f(x)$对应的幂级数，但注意，此时我们不能写成： $f(x)=\sum_{n=0}^\infty{\frac{f^{(n)}(0)}{n!}x^n}$因为即使在收敛半径内，也不一定由此等式成立，那么，满足无穷阶可导的条件，还要满足什么条件才能划上等号呢？我们把在收敛半径内可展称幂级数的无穷阶可导函数称为\underline{实解析函数}，无穷阶可导函数 $f(x)$何时是实解析函数？
实际上，按照Taylor公式，余项可表为 $f(x)-\sum_{k=0}^n{\frac{f^{(k)}(0)}{k!}x^k} =\frac{f^{(k+1)}(\xi)}{(k+1)!}x^{k+1} =\int_0^x{\frac{f^{(n+1)}(t)}{n!}(x-t)^ndt}$我们记余项为 $R_n(x)$，那么，实解析的充要条件是
$\lim_{n\to\infty}{R_n(x)}=0$然而，验证这一条件没有定法，而且不太容易。函数何时解析的问题，在实数域内不能得到彻底的解决，在复变函数论中，这一问题可以就能得到彻底的解决，这不属于数学分析的范畴，这里不详细讲。

初等函数的泰勒展开

例11.1 证明 $f(x)=e^x$是在 $x=0$处是实解析的

证：
幂级数 $\sum_{n=0}^\infty\frac{x^n}{n!}$的收敛域为 $(-\infty,+\infty)$
余项为 $R_n(x) = \frac{e^\xi}{(n+1)!}x^{n+1}$而 $\lim_{n\to\infty}{\frac{x^{n+1}}{(n+1)!}}=0$ $|\frac{e^\xi}{(n+1)!}x^{n+1}|\le \frac{e^{|x|}x^{n+1}}{(n+1)!}$因此， $\lim_{n\to\infty}{R_n(x)}=0$指数函数在其定义域内都可以展开成幂级数。并且 $e^x=\sum_{n=0}^\infty{\frac{f^{(n)}(0)x^n}{n!}}$

例11.2 证明 $f(x)=(1+x)^\alpha$，在 $(-1,1)$上是实解析的

证：
首先，其对应的幂级数为 $\sum_{n=0}^{\infty}{\frac{\alpha(\alpha-1)\cdots(\alpha-n+1)x^n}{n!}}$利用达朗贝尔判别法，容易求得收敛半径为 $1$。
由积分第一中值定理，余项可以表为 $R_n(x)=\int_0^x{\frac{f^{(n+1)}(t)}{n!}(x-t)^ndt} =\frac{(1-\theta)^{n}f^{(n+1)}(\theta x)x^{n+1}}{n!}$其中 $0<\theta<1$，该余项的形式称为柯西余项，我们采用柯西余项： $R_n(x)=\frac{\alpha(\alpha-1)\cdots(\alpha-n)}{n!}(1-\theta)^n(1+\theta x)^{\alpha-n-1}x^{n+1}$由三角不等式，由 $|1+\theta x|\ge 1 - \theta |x| \ge 1-\theta$因此 $|1+\theta x|^{-n-1}\le (1-\theta)^{-n-1}$而 $1-\theta \le |1+\theta x| \le 1+\theta$因此 $|1+\theta x|^\alpha \le \max((1-\theta)^\alpha,(1+\theta)^\alpha)$于是 $|R_n(x)|\le |\frac{\alpha(\alpha-1)\cdots(\alpha-n)}{n!}x^{n+1}|\max((1-\theta)^\alpha,(1+\theta)^\alpha)(1-\theta)^{-1}$由达朗贝尔判别法，容易证明，当 $|x|<1$时，级数 $\sum_{n=0}^{\infty}{\frac{\alpha(\alpha-1)\cdots(\alpha-n)}{n!}x^{n+1}}$绝对收敛，这样就证得了， $|x|<1$时， $R_n(x)\to 0$

例11.3 求 $\ln(1+x)$的幂级数展开

解：
实际上 $\ln(1+x)$的导数为 $\frac{1}{1+x}$，而 $(1+x)^{-1}$在 $(-1,1)$上是实解析的，再用逐项积分的方法，就可以得到 $\ln(1+x) = \sum_{n=1}^\infty{\frac{(-1)^{n-1}x^n}{n}}$类似的方法可以求反三角函数的泰勒级数

魏尔斯特拉斯定理

幂级数是用一系列多项式逼近一个无穷次可微的函数。即如果 $f(x)=\sum_{n=0}^\infty{a_nx^n}$，部分和函数为 $S_n(x)=\sum_{k=0}^n{a_kx^k}$， $S_n(x)$是一个多项式，实际上就是由一系列多项式 $\{S_n(x)\}$去逼近 $f(x)$。对于一般的连续函数，能否做到这一点呢？答案是肯定的。首先，我们给出可由多项式逼近的定义。
定义11.1 $f(x)$在区间 $I$上有定义，如果对任意的 $\varepsilon>0$，存在多项式 $P(x)$，对任意的 $x\in I$，都有 $|f(x)-P(x)|<\varepsilon$则称 $f(x)$在区间 $I$上可被多项式逼近

实际上这个定义就等价于 $f(x)$在区间 $I$上可被一列多项式一致逼近。我们可以给出一个简单的证明：

证：
（1）如果 $f(x)$在区间 $I$上可被多项式逼近，令 $\varepsilon_n=\frac{1}{n}$，存在多项式 $P_n(x)$，对任意的 $x\in I$，都有 $f(x)-P_n(x)<\varepsilon_n$按一致收敛的定义， $P_n(x)$在区间 $I$上一致收敛到 $f(x)$。
（2）如果存在多项式 $P_n(x)$， $P_n(x)$在区间 $I$上一致收敛到 $f(x)$， $\varepsilon>0$，存在 $N$， $n>N$时 $|P_n(x)-f(x)|<\varepsilon$于是 $f(x)$在区间 $I$上可被多项式逼近

若 $f(x)$在区间 $I$上可被多项式逼近，由一致收敛的性质， $f(x)$在区间 $I$上连续。
定理11.6 $f(x)$在无界区间 $I$上可被多项式逼近，则 $f(x)$必为多项式

证：
$f(x)$在无界区间 $I$上可被多项式逼近，则存在一列多项式 $P_n(x)$在区间 $I$上一致收敛到 $f(x)$，由一致收敛的柯西准则，对任意的 $\varepsilon>0$，存在 $N$， $n,m>N$时 $|P_n(x)-P_m(x)|<\varepsilon$假设 $P_n(x)$和 $P_m(x)$是两个不同的多项式， $P_n(x)-P_m(x)$也是一个非零的多项式。若 $P_n(x)-P_m(x)$是一个常数函数，则 $|P_n(x)-P_m(x)|<\varepsilon$，否则，若 $P_n(x)-P_m(x)$的次数至少为1，则 $\lim_{x\to\infty}{|P_n(x)-P_m(x)|}=+\infty$又与 $|P_n(x)-P_m(x)|<\varepsilon$矛盾，因此， $P_n(x)-P_m(x)$是一个常数函数，也就是说， $n>N$时， $P_n(x)$与 $P_{N+1}(x)$只相差一个常数，记 $P_n(x)=P_{N+1}(x)+a_n$，则 $\{a_n\}$收敛， $f(x)=P_{N+1}(x)+\lim_{n\to\infty}{a_n}$，因此 $f(x)$是一个多项式。

现在我们考虑有界区间
定理11.7 $f(x)$在 $(a,b)$上可被多项式逼近，则 $\lim_{x\to a^+}{f(x)}$存在， $\lim_{x\to b^-}{f(x)}$存在，定义
$g(x)=\begin{cases} \lim_{x\to a^+}{f(x)}&x=a\\ f(x)&a<x<b\\ \lim_{x\to b^-}{f(x)}&x=b \end{cases}$ $g(x)$在 $[a,b]$上可被多项式逼近

证：
$f(x)$在 $(a,b)$上可被多项式逼近，则存在多项式 $P_0(x)$，对任意的 $x\in(a,b)$，都有 $|P_0(x)-f(x)|<1$由于 $P_0(x)$在 $(a,b)$上是有界的， $f(x)$在 $(a,b)$上也是有界，不妨设 $|f(x)|<M,\forall x\in (a,b)$，存在一列多项式 $\{P_n(x)\}$， $\{P_n(x)\}$在 $(a,b)$上一致收敛到 $f(x)$。不妨就设 $\forall x \in (a,b)$， $\forall n\ge 1$，都有 $|P_n(x)-f(x)|<1$于是 $|P_n(x)|\le|P_n(x)-f(x)|+|f(x)|< M+1,\forall x \in (a,b),\forall n\ge 1$则 $|P_n(a)|\le M+1,|P_n(b)|\le M+1$，则 $\{P_n(a)\}$和 $\{P_n(b)\}$都有界，取子列 $\{n_k\}$，使得 $\{P_{n_k}(a)\}$和 $\{P_{n_k}(b)\}$都收敛，则 $\{P_{n_k}(x)\}$在 $[a,b]$上一致收敛到 $g(x)$，由于 $\{P_{n_k}(x)\}$在 $[a,b]$上连续，因此 $g(x)$在 $[a,b]$上连续

因此，实际上我们只需要考虑有界闭区间上的连续函数能否被多项式逼近的问题。答案是肯定的，为了解答这个问题，我们需要先给出三个引理。
引理11.2 $f(x)$和 $g(x)$在区间 $I$上可被多项式逼近，则对任意的实数 $a,b$， $af(x)+bg(x)$在 $I$上可被多项式逼近

引理11.3 $f(x)$在 $I$上可被 $\{f_n(x)\}$一致逼近， $\{f_n(x)\}$可被多项式逼近，则 $f(x)$可被多项式逼近

引理11.4 在任意的有界闭区间 $[a,b]$上，对任意的实数 $c$， $|x-c|$在 $[a,b]$上可被多项式逼近

证：
我们先证明 $|x|$在 $[-1,1]$可被多项式逼近，实际上，我们已经证明了 $\sqrt{x+1}=\sum_{n=0}^{\infty}{C_{n}^{\frac{1}{2}}x^n}$收敛半径为 $1$，在 $[0,1]$上一致收敛，于是 $|x| = \sqrt{x^2-1+1} = \sum_{n=0}^{\infty}{C_{n}^{\frac{1}{2}}(x^2-1)^n}$而该级数任意部分和都是多项式，因此， $|x|$在 $[-1,1]$可被多项式逼近，取足够大的 $\beta>0$，使得 $\begin{cases} \frac{b-c}{\beta}\le 1\\ \frac{a-c}{\beta}\ge -1 \end{cases}$则需要 $\beta\ge\max{(b-c,c-a)}$，此时 $|\frac{x-c}{\beta}|$可被多项式逼近，这是因为对任意的 $\varepsilon>0$，存在多项式 $P(x)$， $x\in[-1,1]$时，都有 $||x|-P(x)|<\varepsilon$则 $||\frac{x-c}{\beta}|-P(\frac{x-c}{\beta})|<\varepsilon,\forall x \in [a,b]$而 $P(\frac{x-c}{\beta})$也是多项式，于是 $|x-c|$在 $[a,b]$上也可被多项式逼近

现在我们来整理思路，我们首先证明一类简单的连续函数可以被多项式逼近，然后用这一类简单的连续函数的线性组合去逼近任意的连续函数，从而得出任意的连续函数都可以被多项式逼近的结论。第一类函数是 $max{(x-a,0)}$，其函数图像如下

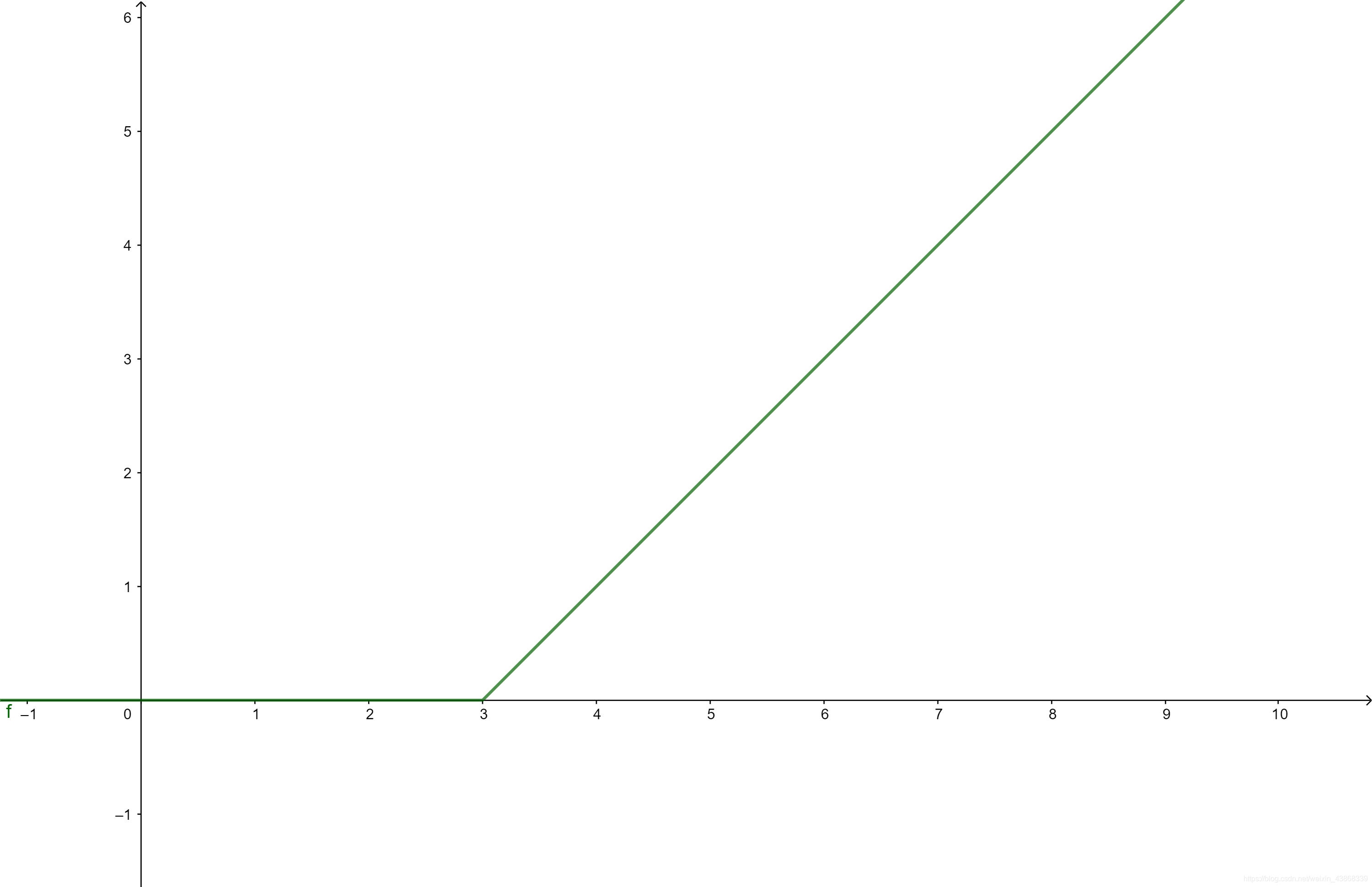
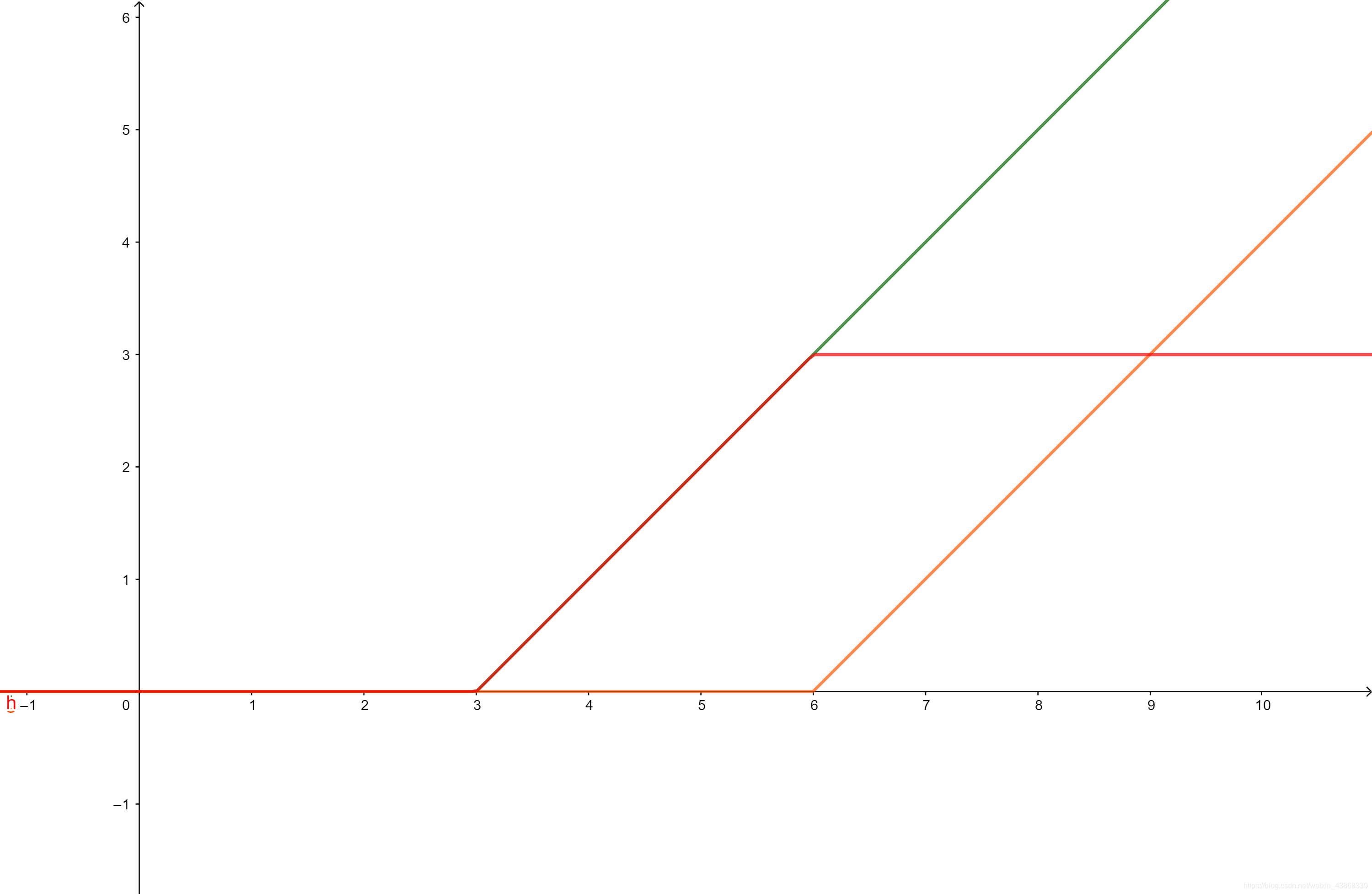
它可以表示成 $H(x,a)=\frac{x-a+|x-a|}{2}$，我们作一个简单的合成， $Q(x,a,b)=H(x,a)-H(x,b)$，就可以得到下图的红色线

接下来我们来考察如何对任意函数进行逼近，一个直观的办法就是利用分段线性函数，如下图所示

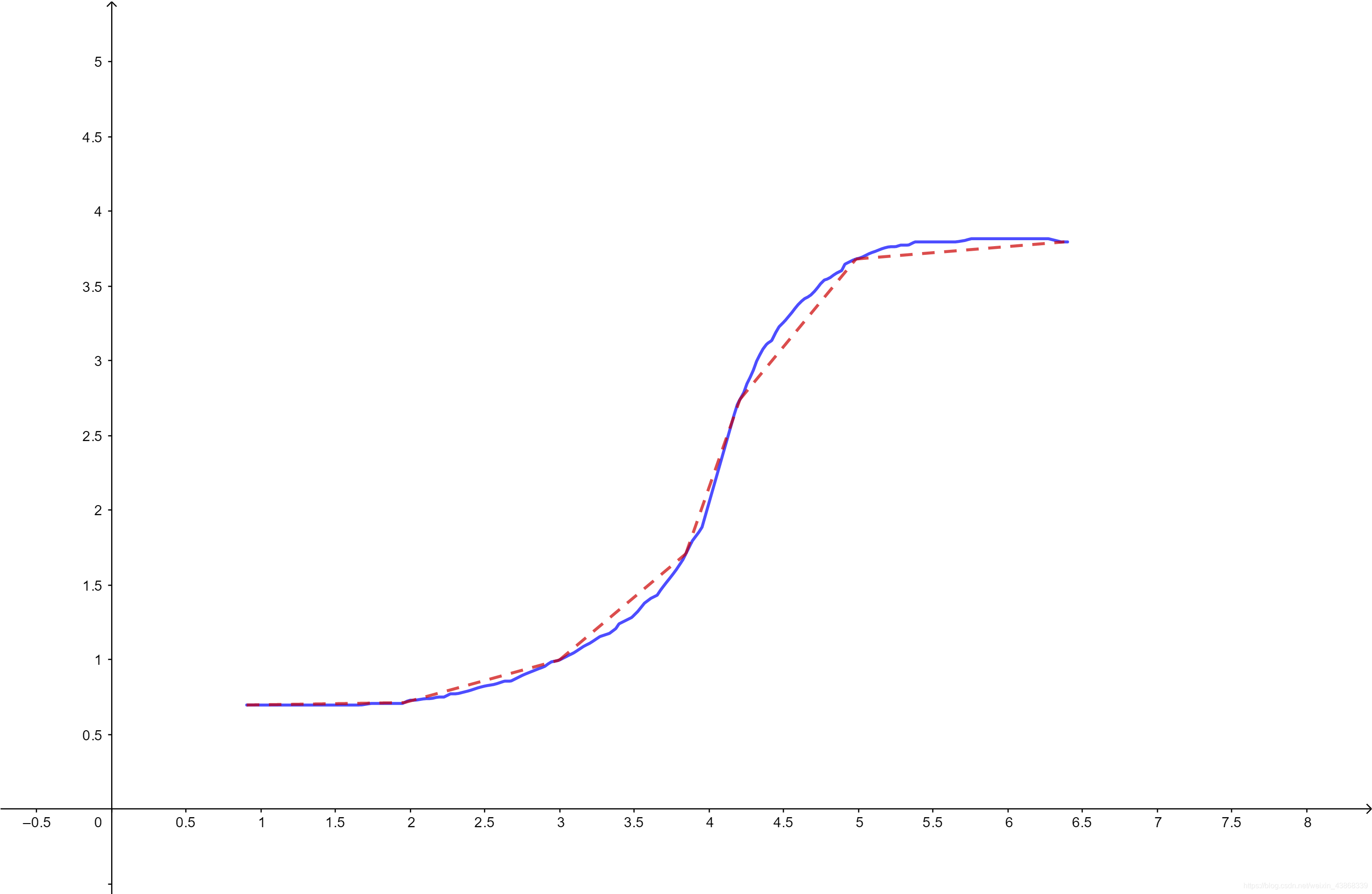
对于蓝色的连续曲线，可以用红色的折线来逼近，当区间越分越细的时候，逼近得就越好，这样，我们就一种逼近方法，我们用分析的语言来把这个想法表达出来。首先我们对区间 $[a,b]$进行划分 $\Delta:a=x_0<x_1<\cdots<x_n=b$，连接 $(x_i,f(x_i))$和 $(x_{i+1},f(x_{i+1})$, $i=1,\cdots,n-1$得到一段折线，这段折线该如何用 $Q(x,a,b)$的语言来表示出来呢？考察函数 $c+kQ(x,a,b)$，则在 $x<a$时， $c+kQ(x,a,b)$是一段平坦的直线 $y=a$，在 $a<x<b$时， $c+kQ(x,a,b)$是一条斜率为 $k$的线段， $x>b$时同样是一条平坦的直线，这就启发我们，这类型的函数首尾相接就可以得到分段线性函数的解析表达式。对 $f(x)$，对分划 $\Delta:a=x_0<x_1<\cdots<x_n=b$，即是 $f(x_0)+\sum_{i=0}^{n-1}{\frac{f(x_{i+1})-f(x_{i})}{x_{i+1}-x_i}Q(x,x_i,x_{i+1})}$，由闭区间上连续的函数的一致连续性，只要 $\Delta$越分越细，分段线性函数可以逼近连续函数，再由前两个引理，即可证得以下定理。
定理11.8（威尔斯特拉斯定理） 闭区间上的连续函数均可被多项式逼近