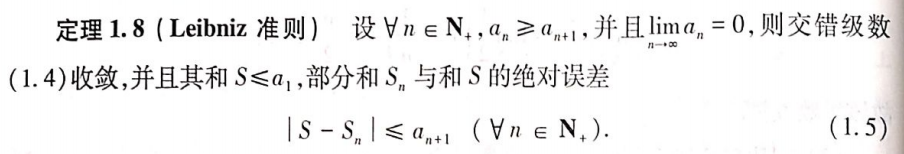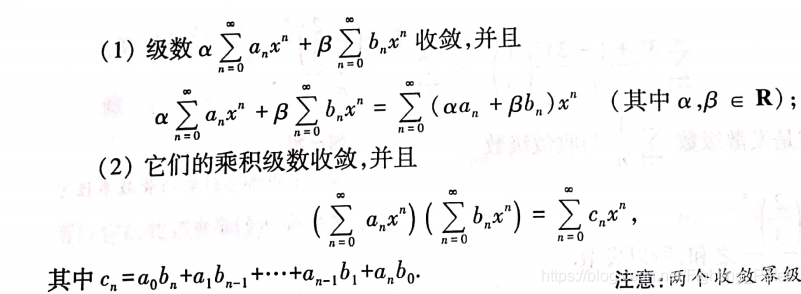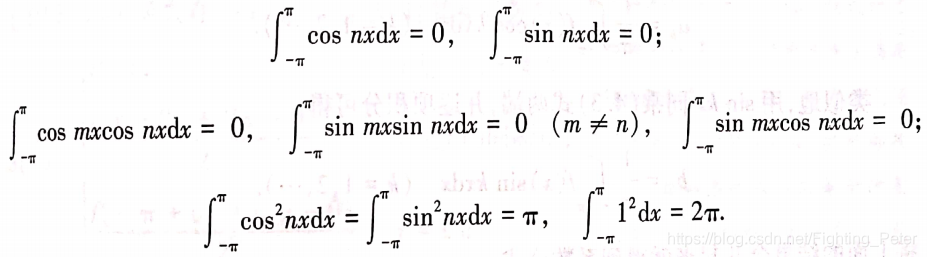工科数学分析无穷级数总结

序言

2020/3/26，老师留了个作业：总结无穷这几周学的无穷级数。由于字太丑所以用一些特别的方式来总结一下吧。

1. 来一个有趣的例子：
   $0.9<1$
   $0.99<1$
   $0.999<1$
   $0.99999<1$
   $0.99999\cdots=1$
   这是我小学就知道的东西，现在到了大学终于明白为什么 $0.99999\cdots=1$
   这里是知乎网友证明 $0.999\cdots=1$的过程
2. 再来一个更贴切点儿点的例子：
   我：小明，咱俩那么好的哥们，我未来会给你一个亿
   小明：好呀好呀！什么时候给我？
   我：未来
   小明：未来是什么时候?
   我：以后再说
   其实我可以到无穷多年之后再给小明这笔巨款，所以小明什么时候能得到？无穷年后？那么他真的会得到这笔巨款吗？哈哈聪明的你可能想到小明根本得不到这笔巨款。 这就我所理解的无穷。

一.常数项级数

概念

1. 什么是常数项无穷级数？

$a_1+a_2+\cdots+a_n+\cdots$，或 $\sum_{n=1}^{ \infty}a_n$称为常数项无穷级数，简称常数项级数或级数， $a_n$称为该级数的通项

2. 级数的收敛性与和

$S_n=a_1+a_2+\cdots+a_n=\sum_{k=1}^{n}a_k$
上述式子称为级数的部分和。若部分和数列{ $S_n$}收敛，则称级数收敛，并称
$S=\lim_{n \to \infty}S_n=\lim_{n \to \infty}\sum_{k=1}^{n}a_k$为他们的和，记作 $\sum_{n=1}^{n \to \infty}a_n=S$；否则称级数发散，级数的收敛与发散成为敛散性收敛级数的和与其部分和之差 $R_n=S-S_n=\sum_{k=n+1}^{\infty}a_k$称为该级数的余项

两个特别的级数

1. 等比级数
   $\sum_{n=0}^{\infty}aq^n=a+aq+aq^2+\cdots+aq^{n-1}+\cdots(a\ne 0)$
   $|q|<1$，等比级数收敛；当 $|q|\ge1$，等比级数发散
2. 调和级数
   $\sum_{n=1}^{\infty}\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}+\cdots$
   为什么叫做调和级数？调和级数发散
   ​

级数的判别方法

①常数项级数判别法

• 定义判别法
• Cauchy收敛原理
  
  每次都有柯西，但是我发现做题很少用柯西的东西

②正项级数的审敛准则

• 正项级数 $\sum_{n=1}^{\infty}a_n$收敛的充要条件是它的部分和数列有上界
• 比较准则 $Ⅰ$

• 比较准则 $Ⅱ$
  

• 积分准则
  

• D’Alembert准则
  

• Cauchy准则
  

• 对数判别法
  

③变号级数的审敛准则

• Leibniz准则
  

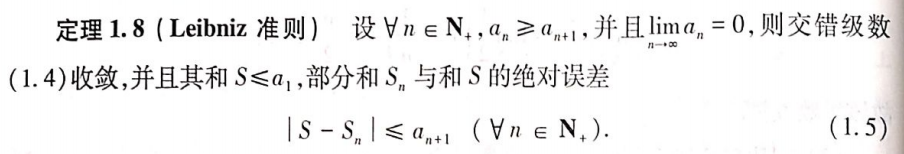
④绝对收敛

• 绝对收敛准则
  若级数 $\sum_{n=1}^{ \infty}|a_n|$收敛，则级数 $\sum_{n=1}^{ \infty}a_n$收敛
• 绝对收敛性质
  $Ⅰ$ $\sum_{n=1}^{ \infty}a_n$绝对收敛，则任意交换它的各项顺序后所得的新级数也绝对收敛，且其和不变；
  $Ⅱ$若级数 $\sum_{n=1}^{ \infty}a_n$和 $\sum_{n=1}^{ \infty}b_n$都绝对收敛，其和分别为 $A$与 $B$，则级数 $\sum_{n=1}^{ \infty}c_n(c_n=a_1b_n+a_2b_{n-1}+\cdots+a_nb_1)$也绝对收敛且其和等于 $AB$。

二.函数项级数

概念

1. 什么是函数项级数？

设{ $u_n$}是定义在同一集合 $A\subset R$上由无穷多项组成的一列函数（称为函数列）将他们各项依次用加号联结起来所得到的表达式 $u_1+u_2+\cdots+u_n+\cdots或\sum_{n=1}^{\infty}u_n$
称为集合A上的函数项级数， $u_n$称为它的通项，前 $n$项之和 $S_n=\sum_{k=1}^{n}u_k$称为它的部分和

2. 函数项级数处处收敛与和函数

设 $x_0\in A$，将 $x_0$代入函数项级数，它就变成一个常数项级数
$\sum_{n=1}^{\infty}u_n(x_0)=u_1(x_0)+u_2(x_0)+\cdots+u_n(x_0)+\cdots$
若该级数收敛，则称 $x_0$为函数项级数的收敛点，由收敛点全体构成的集合 $D$称为该级数的收敛域。若 $x_0$不是收敛点，则称它为该级数的发散点，由发散点的全体所构成的集合称为该级数的发散域。设 $D$为级数的收敛域，则 $\forall x \in D$，级数都收敛，称该级数的这种收敛在 $D$上处处收敛（或逐点收敛）。此时，称由 $S(x)=\sum_{n=1}^{\infty}u_n(x), x \in D$定义的函数 $S$： $D$-> $R$为级数的和函数，简称和。
若级数在 $D$上处处收敛，则 $S(x)= \lim_{n \to \infty}\sum_{k=1}^{n}u_k=\lim_{n \to \infty}S_n(x)$
因此，在 $D$上级数的和函数就是其部分和 $S_n(x)$的极限，与常数项类似，也称
$R_n(x)=S(x)-S_n(x)=\sum_{k=n+1}^{\infty}u_k(x)$为改级数的余项并且 $\lim_{n \to \infty}R_n(x)=0(x \in D)$

一致收敛

1. 函数项级数一致收敛

若存在一个函数 $S$： $D$-> $R$，满足
$\forallε>0$， $\exists N(ε) \in N_+$，当 $n>N(ε)$时， $\forall x \in D$，恒有 $|S(x)-S_n(x)|$，称级数在 $D$ 上一致收敛于 $S$

2. 函数项级数一致收敛判别准则

• Cauchy一致收敛原理
  
• Weierstrass 准则
  

3. 函数项级数一致收性质

• 和函数的连续性
  

• 和函数的可积性
  

• 和函数的可导性
  

三.幂级数

概念

什么是幂级数?

形如
$\sum_{n=1}^{\infty}a_nx^n=a_0+a_1x+a_2x^2+\cdots+a_nx^n+\cdots$
或者
$\sum_{n=1}^{\infty}a_n(x-x_0)^n=a_0+a_1(x-x_0)+a_2(x-x_0)^2+\cdots+a_n(x-x_0)^n+\cdots$的函数项级数称为幂级数

收敛半径

1.什么是收敛半径?

收敛半径r是一个非负的实数或无穷大，使得在 $|z-a| < R$时幂级数收敛，在 $|z -a| > R$时幂级数发散。

2.求收敛半径

• 比值求法
  设有幂级数 $\sum_{n=0}^{\infty}a_nx^n$，若 $a_n\neq 0$，并且 $\lim_{n \to \infty}|\frac{a_n}{a_{n+1}}|$存在或为 $+\infty$则它的收敛半径为 $R=\lim_{n \to \infty}|\frac{a_n}{a_{n+1}}|$

• 根值求法
  设有幂级数 $\sum_{n=0}^{\infty}a_nx^n$，若 $a_n\neq 0$，并且 $\lim_{n \to \infty}|\frac{1}{\sqrt[n]{a_n}}|$存在或为 $+\infty$则它的收敛半径为 $R=\lim_{n \to \infty}|\frac{1}{\sqrt[n]{a_n}}|$

幂级数性质

1.代数运算性质

设幂级数与的收敛半径分别为 $R1$与 $R2$，令 $R=min(R1,R2)$，则在它们的公共收敛区间 $(-R,R)$内，有

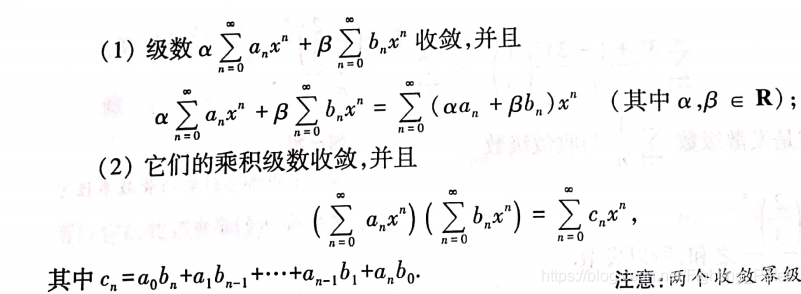
2.和函数的性质

• 和函数的可积性
  
• 和函数的可导性

常见麦克劳林级数

• 几何级数
  $\frac{1}{1-x}=1+x+x^2+\cdots+x^n+\cdots,|x|<1$

• 指数函数 $e^x$展开式
  $e^x=1+x+\frac{x^2}{2!}+\cdots+\frac{x^n}{n!}+\cdots,x\in(-\infty,+\infty)$

• 正弦 $sinx$展开式
  $sinx=x-\frac{x^3}{3!}+\frac{x^5}{5!}+(-1)^k\frac{x^{2k+1}}{(2k+1)!}+\cdots,x\in(-\infty,+\infty)$

• 余弦函数 $cosx$展开式
  $cosx=1-\frac{x^2}{2!}+\frac{x^4}{4!}+(-1)^k\frac{x^{2k}}{(2k)!}+\cdots,x\in(-\infty,+\infty)$

• 对数函数 $ln(x+1)$展开式
  $ln(x+1)=x-\frac{x^2}{2}+\frac{x^3}{3}+(-1)^{n-1}\frac{x^n}{n}+\cdots,x\in(-1,1]$

• 幂函数 $(1+x)^a$的展开式 $(a\in R)$
  $(1+x)^a=1+ax+\frac{a(a-1)}{2!}x^2+\cdots+\frac{a(a-1)\cdots(a-n+1)}{n!}x^n+\cdots,x\in(-1,1)$

四.傅里叶级数

三角函数的正交性

1.三角函数系

{ $1,cosx,sinx,cos2x,sin2x,\cdots,cosnx,sinnx,\cdots$}

2.正交性

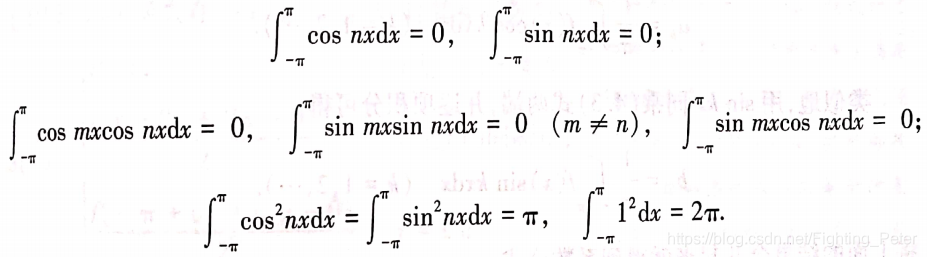
Dirichlet定理与条件

傅里叶级数展开

1.定义在 $[-l,l]$上函数的Fourier展开

$f(x)=\frac{a_0}{2}+ \sum_{n=1}^{\infty}(a_ncos\frac{nπx}{l}+b_nsin\frac{nπx}{l})$
其中系数 $a_n$和 $b_n$可由下面的公式求的

$\begin{cases} a_n=\frac{1}{l} \int_{-l}^{l} f(x)cos\frac{nπx}{l}dx (n=0,1,2,\cdots) \\ b_n=\frac{1}{l} \int_{-l}^{l} f(x)sin\frac{nπx}{l}dx (n=1,2,3,\cdots)\end{cases}$

2.定义在 $[0,l]$上函数的Fourier展开

• 偶延拓
  如果要求将 $f$在 $[0,l]$展开成Fourier余弦函数，可采用偶延拓的方式
  $F(x)=\begin{cases} f(x),0\leq x \leq l \\ f(-x),-l\leq x < 0\end{cases}$
  将 $F$在 $[-l,l]$上展开成Fourier级数，得
  $\begin{cases} a_n=\frac{2}{l} \int_{0}^{l} f(x)cos\frac{nπx}{l}dx (n=0,1,2,\cdots) \\ b_n=0 (n=1,2,3,\cdots)\end{cases}$
  从而得知
  $f(x)=\frac{a_0}{2}+ \sum_{n=1}^{\infty}a_ncos\frac{nπx}{l}$
  就是 $f$在 $[0,l]$上的Fourier余弦展开式
• 奇延拓
  如果要求将 $f$在 $[0,l]$展开成Fourier余弦函数，可采用偶延拓的方式
  $F(x)=\begin{cases} f(x),0<x \leq l \\ -f(-x),-l\leq x < 0\end{cases}$
  将 $F$在 $[-l,l]$上展开成Fourier级数，得
  $\begin{cases} a_n=0 (n=0,1,2,\cdots) \\ b_n=\frac{2}{l} \int_{0}^{l} f(x)sin\frac{nπx}{l}dx (n=1,2,3,\cdots)\end{cases}$
  从而得知
  $f(x)= \sum_{n=1}^{\infty}b_nsin\frac{nπx}{l}$
  就是 $f$在 $[0,l]$上的Fourier余弦展开式

总结

学的不咋好，上网课太难专注了，就这样吧。如有错误请指正。
图片来源于百度百科和工科数学分析电子课本
如果转载请注明