数学分析- 微分中值定理

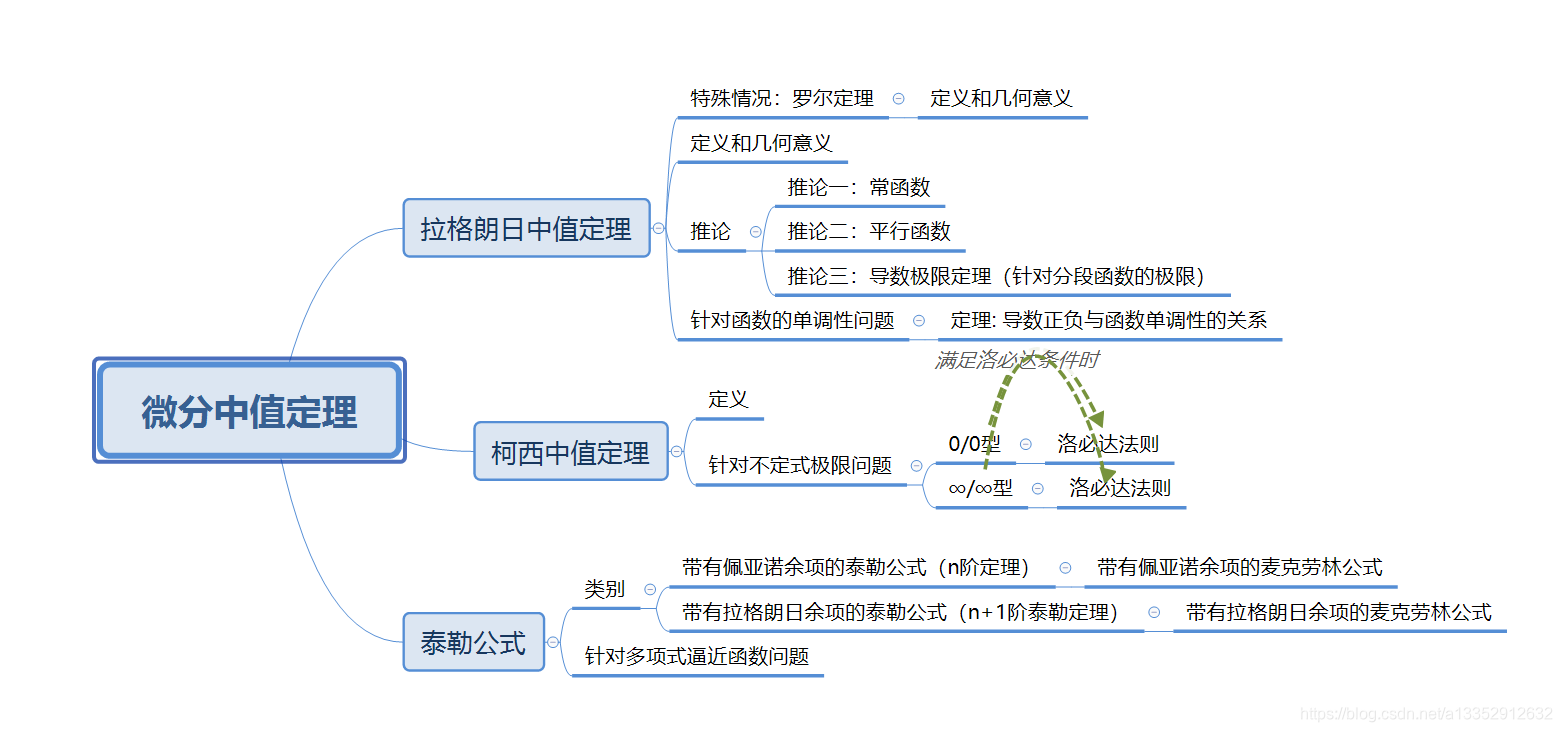
微分中值定理（有关导数的定理）

简介：
这一章将讨论的时由导数 f ’ 的已知性质来推导函数 f 的性质
讨论的工具是关于函数导数的微分中值定理（包括罗尔定理，拉格朗日定理，柯西定理，泰勒定理），名字中的中值指的是定义域中的值
罗尔定理，拉格朗日定理 ----> 函数单调性问题
柯西定理 ，(洛必达法则) ----> 函数不定式极限问题
泰勒定理 ----> 函数的近似(逼近)问题

---

罗尔定理和拉格朗日定理 / 函数的单调性

|| 定理1：罗尔中值定理
若函数 f 满足以下3个条件：

• f在闭区间 [ a, b ] 上连续
• f在开区间 ( a, b) 上可导
• f（a） = f（b）

则在(a, b)上至少存在一个数∮，使得f ‘（∮） = 0

（注意：如果要方便记忆条件的话：）

1. 区间[a, b]内认真考虑（[a, b]连续可导），区间之外忽略考虑（去掉点a，点b可导性）
2. f（a） = f（b）

|| 罗尔中值定理的几何意义
在每一点都可导的一段连续曲线上，如果曲线的两端高度相等，则至少存在一个点有水平切线(与x轴平行的切线)

|| 定理2：拉格朗日中值定理
若函数 f 满足以下2个条件：

• f在闭区间 [ a, b ] 上连续
• f在开区间 ( a, b) 上可导
  则在(a, b)上至少存在一个数∮，使得f ‘（∮） = f(b) - f(a) / b - a （拉格朗日公式）

（注意：容易看到罗尔中值定理是拉格朗日中值定理当f(a) = f(b)的特殊形式）

|| 拉格朗日中值定理的几何意义
在每一点都可导的一段连续曲线上，至少存在一个点的切线平行于端点AB的连线

扫描二维码关注公众号，回复： 11591359 查看本文章

|| 中值点∮的表示方法：
除了∮ ∈(a, b)，还可以表示成 ∮ = a + h(b - a) , h∈(0,1)
好处：使得a，b两个数字不需要特定的大小关系。
在程序中使用这样的表示 “ 值的范围 ”的数学形式会更漂亮

|| 拉格朗日中值定理的推论：

1. 若函数f在区间 I 上可导，且所有f '(x) = 0，则f 是 I 上的一个常量函数
2. 若函数 f 和 g 均在区间 I 上可导，且所有f '(x) = g’（x），则 f(x) = g(x) + c(常数)
3. (导数极限定理）若函数f在U(x₀) 内连续，且在U⁰(x₀)内可导，且极限lim_x–>x0f‘(x)存在
   那么f在x0上就是可导的，且f’（x0） = lim_x–>x0f‘(x)

（注意：推论三往往运用于求分段导数中的某点的导数。方便记忆：f 在U⁰(x₀)上可导，若在x₀上连续且存在导数极限lim_x–>x0f‘(x)，那么f在x0上就是可导的，且f’(x0)就等于该导数极限）

|| 当在U小邻域中使用拉格朗日中值定理时，可以获得导数的表达式 :lim_x–>x0f(x) - f(x0) / x -x0 = lim_x–>x0f(∮)

单调函数

|| 定理3：单调性和导数的关系
设函数f（x）在区间 I 上递增（减）的充要条件是：f’ (x) ≥ 0,x∈ I

|| 推论：严格单调性和导数的关系
若函数 f 在( a, b)内可导，设函数f（x）在区间 I 上递增（减）的充要条件是：f’ (x) > 0,x∈ I

---

柯西中值定理和不定式极限

简介：柯西中值定理和以其为依据的洛必达法则，解决有关不定式极限的问题

|| 定理4：柯西中值定理
若函数 f 和 g 满足以下4个条件：

• 都在闭区间 [ a, b ] 上连续
• 都在开区间 ( a, b) 上可导
• f ’（x）和 g ’（x）不同时为0 （即f 和 g 不同时达到极大值）
• g ( a ) != g ( b )

则在(a, b)上存在数∮，使得 f ’（∮）/ g ’（∮） = f(b) - f(a) / g(b) - g(a)

(注意：方便记忆，存在一个x使得 “两个函数的导数比” 等于 “函数端点函数值（或端点连线斜率）之差的比 ”)
(注意：证明，要引入一个辅助函数F(x))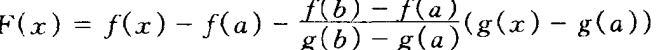

不定式极限

|| 什么是不定式极限
求极限运算时若包含无穷大/小量，极限可能存在也可能不存在（0*∞, 1^∞, 0⁰, ∞⁰, ∞ - ∞）故称为不定式极限
两个无穷小量之比和两个无穷大量之比的极限，可以对应分为 0/0和∞/ ∞两种基本类型的不定式极限
（极限可以分为两种非不定式极限和不定式极限）

|| 洛必达法则的使用条件
比式是一个不定式，且满足对应形式的洛必达的第二个邻域可导性条件

|| 定理5：洛必达法则（0/0型）
若函数 f，g满足以下2个条件：

• lim_x–>x0f(x) = lim_x–>x0g(x) = 0 （保证是0/0型不定式）
• 在点x0的空心邻域U⁰(x₀)都可导，且g’（x）!= 0
  则lim_x–>x0f（x）/g（x），= lim_x–>x0f’（x）/g’（x）= A（可以是常数，也可以是∞）

|| 定理6：洛必达法则（∞/∞型）
若函数 f，g满足以下3个条件：

• lim_x–>x0f(x) = lim_x–>x0g(x) = ∞
• 在点x0的右邻域U⁰₊(x₀)都可导，且g’（x）!= 0

则lim_x–>x0f（x）/g（x），= lim_x–>x0f’（x）/g’（x）= A（可以是常数，也可以是∞）

|| 不定式极限的转换
各种不定式极限的类型（0*∞, 1^∞, 0⁰, ∞⁰, ∞ - ∞），都能通过简单的变换 ( 化为自然对数e的指数形式，化作比值形式，通分等操作 )，化为0/0，∞/∞两种类型的不定式极限

---

泰勒公式和函数的多项式逼近

简介：下文的T_n(x)都代表函数 f 的泰勒多项式

|| 多项式逼近函数的思想
在前面研究导数和微分时，式子 f(x) = f(x₀) + f’(x₀)(x - x₀) + o(x - x₀)，就是使用一次多项式 f(x₀) + f’(x₀)(x - x₀)去逼近函数f（x），误差为x - x₀的高阶无穷小量。
为了更好地逼近函数，我们可以用二次甚至更高次的多项式去逼近，以产生更小的误差（o(x-x₀)ⁿ）

带有佩亚诺余项的泰勒公式

书上解释得很好，直接在这里引用了。图中的p_n(x)为任一个n次多项式

总结一下：对任一个n次多项式逐项求导时，会发现多项式的每个项系数与在点x0上导数值有关。
通过在点x0上不同阶的导数代表不同次的项，来组成n次多项式代表函数 f ，则
该多项式就称为f在点x0处的泰勒多项式，
泰勒多项式的各项系数（f^(k)(x₀) / k!, k = 1,2,…,n）就称为泰勒系数，
产生的误差（例如：o(x - x₀)ⁿ），称作泰勒公式的余项R_n（x）。
泰勒公式： f （x）= T_n（x）+ R_n（x）

（注意1：带有形如o(x - x₀)ⁿ余项的泰勒公式称为 带有佩亚诺余项的泰勒公式）
（注意2：当 f（x）= p_n（x）+ R_n（x）时，p_n（x）为 T_n（x）或者 0，但是若 f 满足了定理7的条件，则p_n（x）必为为 T_n（x））

|| 定理7：泰勒多项式的逼近情况（n阶定理）
若函数 f 在点x0存在直至n阶的导数，则有f（x）= T_n（x） + o(x-x₀)ⁿ

|| 带有佩亚诺余项的泰勒公式的特殊形式（当x₀ = 0）：带有佩亚诺余项的麦克劳林公式

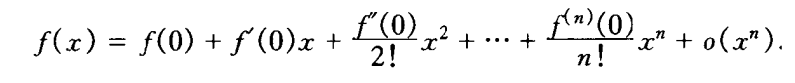
带有拉格朗日余项的泰勒公式

|| 拉格朗日余项和佩亚诺余项的区别：
佩亚诺余项，定性地说明误差是个高阶无穷小量，拉格朗日余项，可以定量地说明误差

|| 定理8：泰勒定理（带有拉格朗日余项的泰勒公式定理）
若函数 f 在 [ a, b ] 存在直至n阶的连续导数，在（a，b）内存在n+1阶导函数，则对任给定的x,x₀∈[a , b]，至少存在一点∮∈ (a , b)，使得:

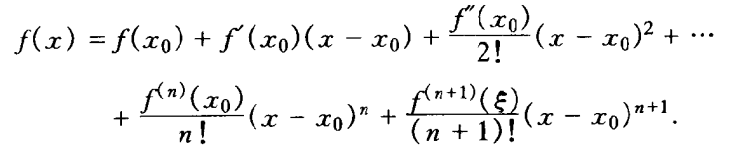
该式子即为带有拉格朗日余项的泰勒公式
上式中的最后一项的即为带有拉格朗日余项的泰勒公式的拉格朗日余项

|| 带有拉格朗日余项的泰勒公式的特殊形式（当x₀ = 0）：带有拉格朗日余项的麦克劳林公式