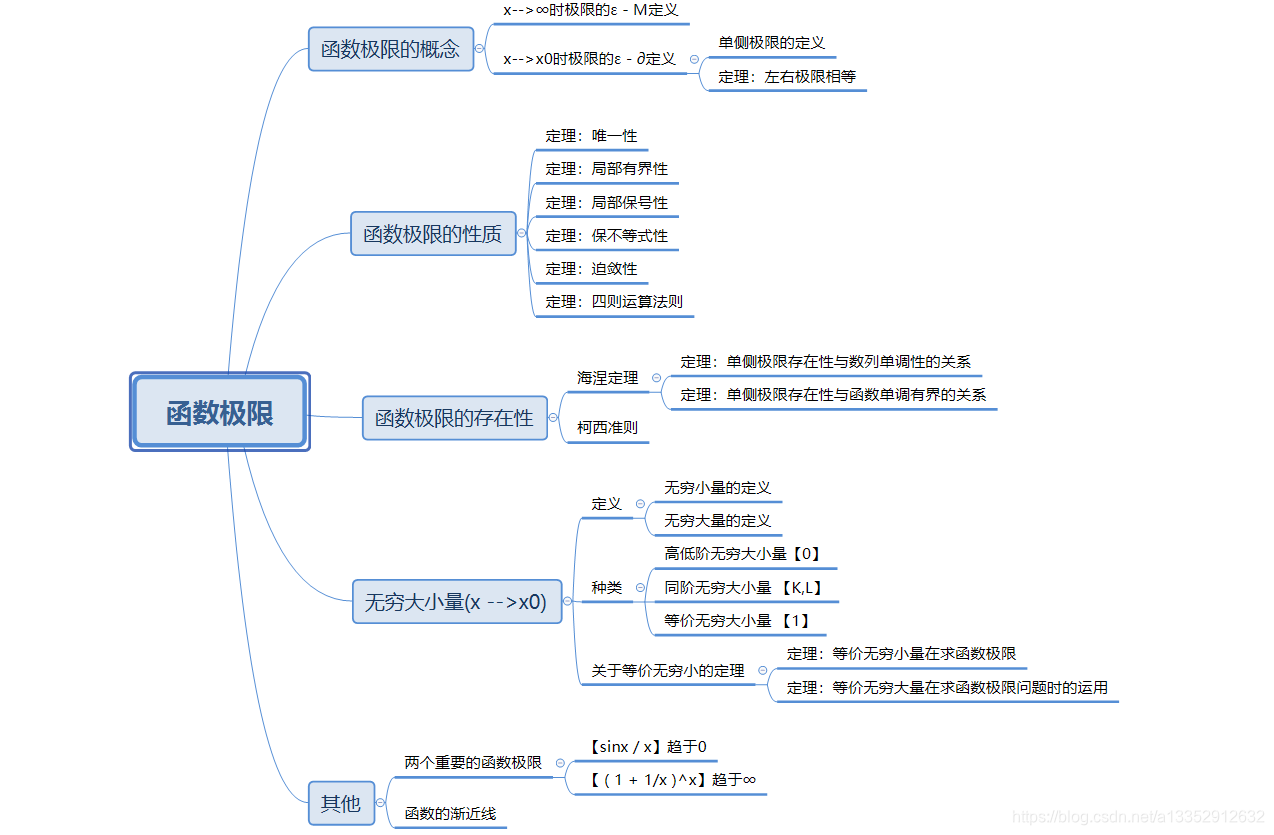
函数极限的概念
x趋于∞时的极限
|| 定义一:函数极限的ε - M定义
设f为定义在[a,+∞)上的函数,A为定数,若对任给的ε>0,存在正数M(≥a),使得当x>M时有 |f (x) - A| < ε,则称函数f当x趋于+∞时以A作为极限,记作:
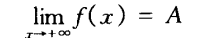
x趋于x0时函数的极限
|| 定义二:x趋于x0时函数极限的ε - ∂定义
设函数f在点x0的某个空心领域U0(x0, ∂)内有定义,A为定数,若对任给的的ε>0, 都存在正数∂,得当0<|x - x0 |<∂时有 |f(x) - A| < ε,则称函数f当x趋于x0时以A为极限,记作:
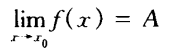
|| 定义三:x趋于x0时函数单侧极限:
设函数在x0的某个空心邻域U0-(x0, ∂)内有定义,A为定数,若对任给的ε>0, 都存在正数∂,使得x0-∂ < x < x0时有 |f(x)- A| < ε,则称数A为函数f当x趋于x0-时的左极限,记作:
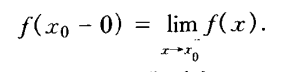
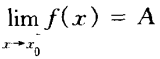
|| 定理1:函数趋于x0的极限为A的充要条件为函数趋于x0的左右极限都为A
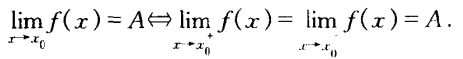
函数极限的性质
注意:我们使用函数趋于点x0的极限来研究函数任何类型极限的性质
定理2:唯一性
若函数极限limx->x0f(x)存在,那么此极限是唯一的
定理3:局部有界性
若函数极限limx->x0f(x)存在,则f在x0的某空心邻域中有界
定理4:局部保号性
若函数极限limx->x0f(x) = A>0,则对任何正数r<A,存在U0(x0),使得对一切x∈U0(x0)有f(x)>r>0
定理5:保不等式性
若limx->x0f(x)与limx->x0g(x)都存在,且在某邻域U0(x0; ∂),内有f(x) ≤ g(x),则limx->x0f(x) ≤ limx->x0g(x)
定理6:迫敛性
设limx->x0f(x) = limx->x0g(x) = A,且在某邻域U0(x0; ∂)内有f(x) ≤ h(x) ≤ g(x),则limx->x0h(x) = A
定理7:四则运算法则:
若极限limx->x0f(x)与limx->x0g(x)都存在,则函数f ± g,f * g当x–>x0时极限也存在,且有
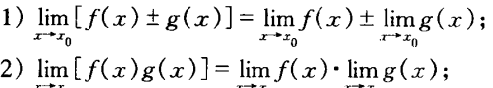
若limx->x0g(x) != 0,则f/g当x–>x0时极限也存在,且有
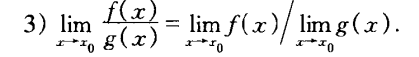
函数极限存在的条件
同数列极限存在性的研究一样,我们将利用函数的本身特征(函数值的变化趋势)来判断函数极限的存在性
|| 定理8:海涅Heine定理(归结原则)
设f在U0(x0; ∂)内有定义,limx->x0f(x)存在的充分必要条件是:
对于任何对任何内含于U0(x0; ∂)且以x0为极限的数列{xn},极限limn->∞f(xn)都存在且相等
(通过数列达到x趋近于x0,且有多个该值的效果,再代入函数f判断这些值有无相同的值,即极限)

|| 海涅定理的意义在于把函数极限归结为数列极限问题来证明
|| 定理9:对于单侧极限的存在性的海涅定理
设函数f在点x0的某空心邻域U0+(x0; ∂)有定义,limx->x0+f(x) = A 的充要条件是:对任何以x0为极限的且含于U0+(x0; ∂)递减数列{xn},有limn->∞f(xn) = A
(递减数列保证了所有数列值都是大于x0的)
|| 定理10:
设f 为定义在U0+(x0; ∂)上的单调有界函数,则右极限limx->x0+f(x) 存在
|| 定理11:柯西准则
设函数f在U0(x0; ∂)内有定义,limx->x0f(x)存在的充分必要条件是:
任给的ε>0, 都存在正数∂,使得对任何x1,x2∈U0(x0; ∂),有 | f(x1) - f(x2)| < ε .
两个重要的极限
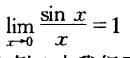
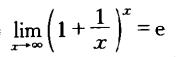
无穷小量和无穷大量
无穷小量
|| 定义四:无穷小量的定义(类似于无穷小数列)
某函数f在U0(x0)内有定义,若limx–>x0f(x)= 0,则称f为当x–>x0时的无穷小量
若函数是有界函数时,则称f为当x–>x0的有界量
(注意: 无穷小量就是在x0以0为极限的函数)
|| 推论:
limx–>x0f(x)= A 《==》 函数 f(x) - A 称为当x–>x0时的无穷小量
无穷小量的阶,与阶的比较
(虽然无穷小量都是以0为极限的函数,但是它们趋近于0的速度是不一样的)
|| 定义五:高阶无穷小量与低阶无穷小量的定义
若f,g都是x–>x0的无穷小量,limx–>x0 [f(x)/ g(x)] = 0,则称当x–>x0时,f为g的高阶无穷小量,g为f的低阶无穷小量,记作:
f( x ) = o( g(x) ) ( x–>x0 ) (等号" = "理解为“属于”, o( g(x) )是满足以上条件的函数的集合)
(注意:即越高阶的无穷小量处于0的速度越快)
|| 定义六:同阶无穷小量的定义
f,g都是x–>x0的无穷小量,若存在整数K,L,使得在U0(x0)上有:K ≤ | f(x)/ g(x) | ≤ L
(注意:当商的极限不为0,且不为1时,则称f,g为同阶无穷小量)
|| 定义六的扩展:大O表示
只要满足 | f(x)/ g(x) | ≤ L,就可记作: f(x) = O( g(x) ) ( x–>x0 ) (等号" = "理解为“属于”, o( g(x) )是满足以上条件的函数的集合)
|| 定义七:等价无穷小量
f,g都是x–>x0的无穷小量,若limx–>x0 [f(x)/ g(x)] = 1,则称当x–>x0时,f与g的是x–>x0时的等价无穷小量,记作: f( x ) ~ g ( x ) (x --> x0)
|| 注意事项:
- 无穷小量指的是函数,无穷小数列指的是数列,而无穷大量可以指数列也可以指函数
- 方便记忆:同阶无穷小量是有倍数关系的等价无穷小量
- 并不是所有无穷小量都可以进行阶的比较,需要满足x–>x0时它们的比值极限是有界量的条件
定理12:等价无穷小量在求函数极限问题的应用
设函数f,g,h在U0(x0)上都有定义,且f(x) ~ g(x) (x --> x0),则:
- 若limx–>x0f(x) h(x) = A, 则limx–>x0g(x) h(x) = A
- 若limx–>x0h(x) / f(x) = B,则limx–>x0h(x) / g(x) = B
无穷大量
|| 定义八:非正常极限∞的定义
设函数f 在U0(x0)上有定义, 若对于任给的G > 0,都存在有∂ > 0, 使得x∈U0(x0,∂)时,有| f(x) | > G ,称啊哈纳树f当x–>x0时有非正常极限∞,记作: lim~x -->x0~f(x)= ∞。
若 f(x) > G 或 f(x)< -G 时,有 极限+∞ 或 极限-∞
|| 定义九: 无穷大量的极限
所有以∞,+∞,-∞为非正常极限的函数(或者数列),都可以称为无穷大量。
(注意:无穷大量指的是有非正常极限的函数或者和数列,不是指很大的数)
|| 无穷大量中的高低阶无穷大量,同阶无穷大量,等价无穷大量的定义同无穷小量类似
|| 定理13:等价无穷大量在求函数极限问题时的运用
若函数f在U0(x0)上有定义且不为0,那么
- 若f在x–>x0时为无穷小量,则 1 / f 在x–>x0时为无穷大量
- 若f在x–>x0时为无穷大量,则 1 / f 在x–>x0时为无穷小量
函数的渐近线
|| 定义九:函数的渐近线的定义
若函数曲线C上的动点P沿着曲线无限地远离原点时,p点与直线L的距离无限接近于0,则称直线L为曲线的渐近线
|| 斜渐近线与垂直渐进线的求法
