线性代数里面蕴含着丰富的数形结合思想,结合图形来理解,难度会小很多,以下证明不一定严密,但至少不依赖任何技巧的花哨的数学方法,依赖空间直觉得出自然而然的结论,学习线性空间理论,应该低起点,高观点。
0.0结合律的证明,同济教材只给出了结论,并没有证明.
矩阵:
为一
矩阵,
为一
矩阵,
为一
矩阵,令
则,需要证明,根据矩阵的乘法定义:
的
元为:
的
元为:
由于
所以:
QED!
0.1为一
矩阵,则
很普通的定理,还是要证一下:
采用数学归纳法证明对于n阶矩阵是成立的,显然,因为阶矩阵是对称的标量,结论对于
是成立的,假设这个结论对于所有的
也是成立的,则,对于
阶矩阵A,将
按照A的
第一行展开,有:
为
矩阵,由归纳假设得
恰好是按照
的第一列代数余子式展开,因此
QED!
1.在线性空间的理论中,有一个定理起着重要的作用,描述如下,如果向量组

中每一个向量都是向量组

的线性组合,而且m>k,则向量

必定线性相关.
证明过程如下,由题设:
必然存在KxK的满秩矩阵A,使得

是

空间向量的线性变换结果,也即是:
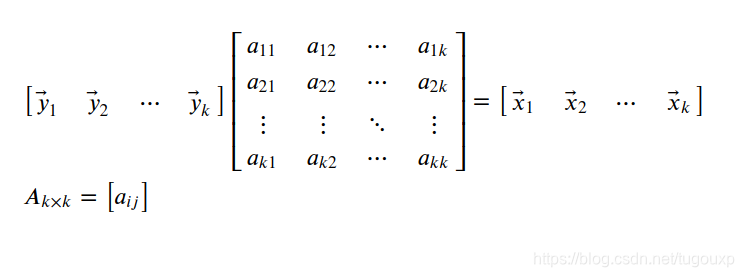
这样
 和
和  均可以做为K维空间的基.
均可以做为K维空间的基.
所以, 和
和 也必然存在逆变换B,使得
也必然存在逆变换B,使得
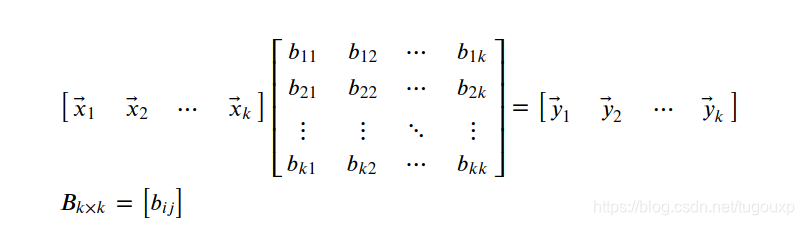
其中

A,B互逆.
也就是说,不但x向量可以由y表示,而且也可以反过来标识y向量,两者在空间中是等价的,只是观察角度不同(玩儿游戏的同学应该能懂,吃鸡报点:))
所以,在K维空间中,哪怕在多一个向量,必定可以由k维的基标识,所以
m>k的情况下,多出来的m-k个向量必然可以被表示出来。
证毕:
对于上面证明用到的一个引理,就是为什么要求A矩阵一定满秩,简单证明如下:
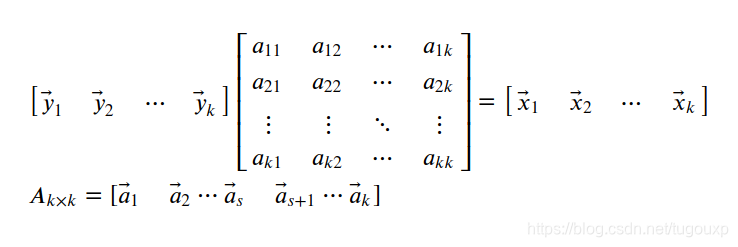
其中

线性无关,其余向量可由其标识:

所以:

则x 必然也线性相关,引理得证明。
QED!
人类只能理解三维以下的空间,高维空间到底是什么样子的呢? 好想知道
2.关于空间中的坐标变换:
将z=4x+5y通过坐标变换变成简单形式。
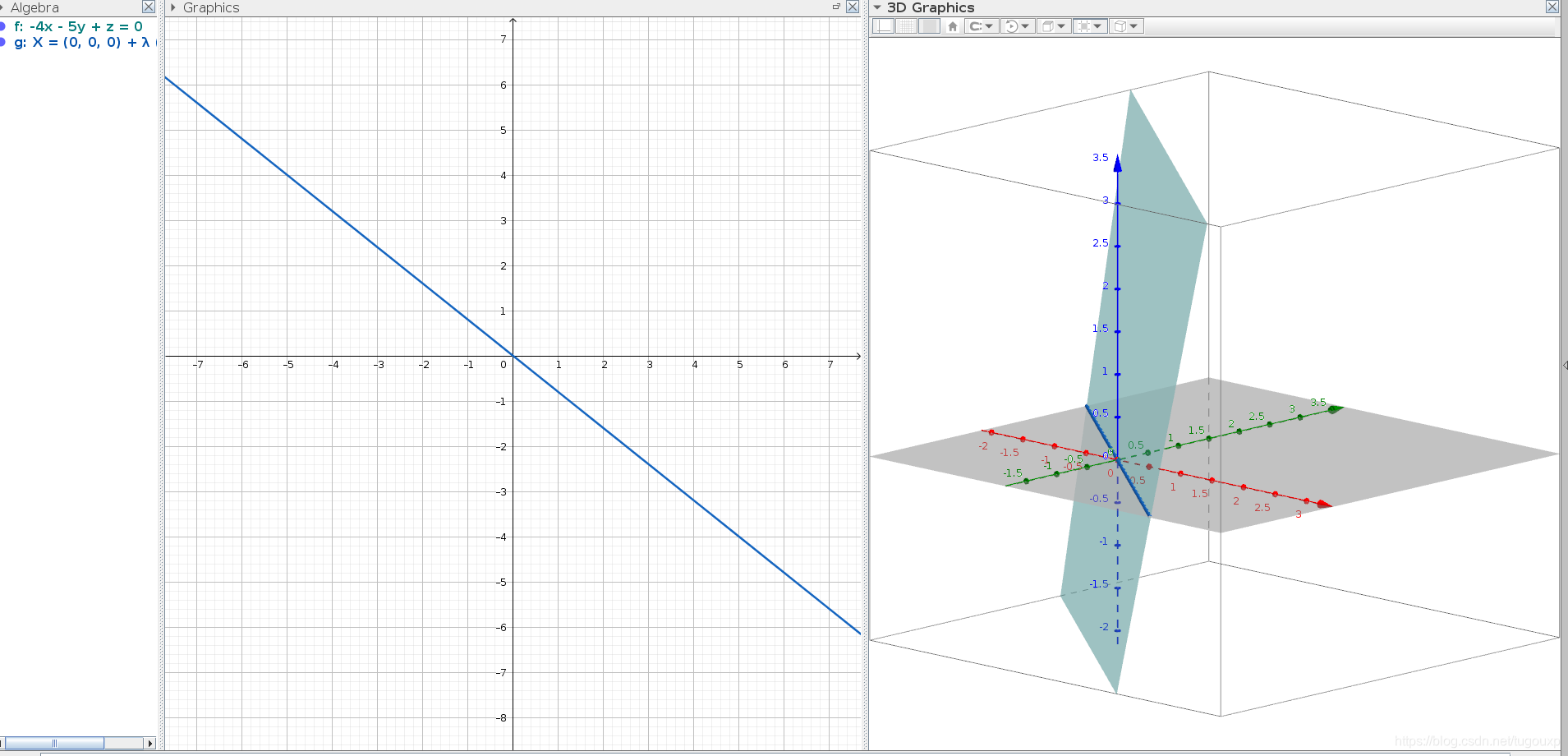
首先可以选择平面上的两个点:
比如(1,1,9)以及(2,1,13)

首先,将两个向量施密特正交化:
施密特正交化后得到:
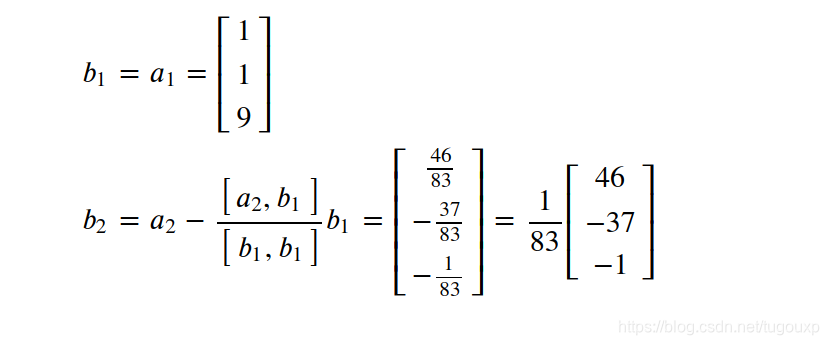
我们主要关心方向:

将向量规范化为:
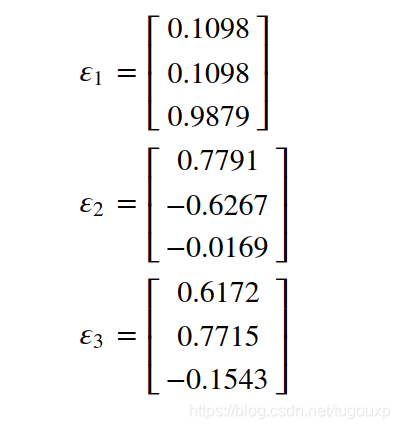
则:

所以,
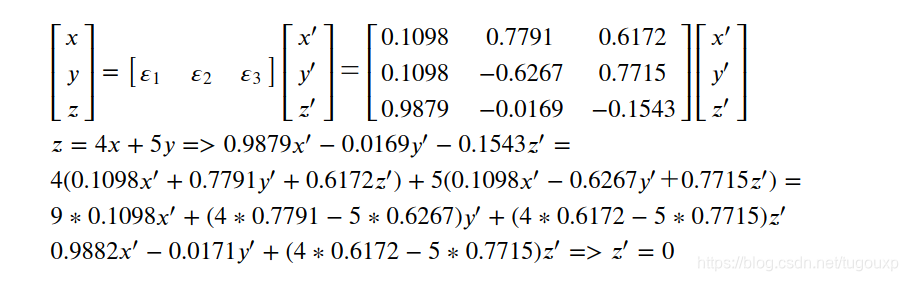
去掉误差项0.0003以及0.0002后,消失了两个维度,得到简化的平面方程
![]()
空间变换是一种很重要的数据处理思想,一些看似杂乱的数据,如果换一个角度去看,在高纬度的可能存在规律的形状, 要仔细领会。
3.线性空间中有一个非常基础的论断,就是矩阵中行秩必定等于列秩,而且课本给出了证明。
看似简单,但行秩为什么必须等于列秩呢? 它究竟反应的是空间的什么结构性质呢?
对于矩阵来说,行秩=列秩,等价于说,如果行线性相关,那么列必定也线性相关,行和列不是一回事呀,包含的元素也不相同,为什么呢? 先通过一个三维空间中的例子来验证这个结论:
如下矩阵,很明显,前两行具有完全的自由度,不会线性相关,第三行由前两行线性组合而成,所以行向量必定线性相关。

列向量是否线性相关,完全看不出任何规律,不明显,我们需要变化一下:

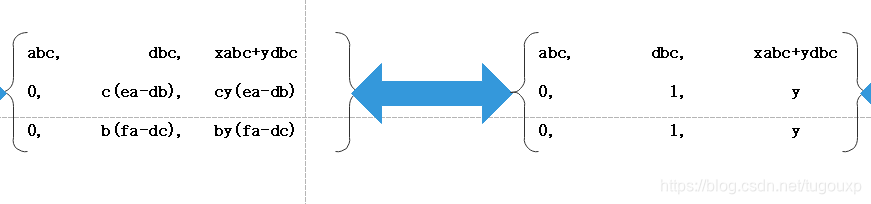


所以,看一看出来,转置矩阵,经过初等行变换后,最后一行简化为0,对应的原来矩阵列线性相关。
所以,原来矩阵 行线性相关<=====>矩阵列线性相关,两个等价。
上面的初等行变换过程是:


所以,行线性相关得证:
或者
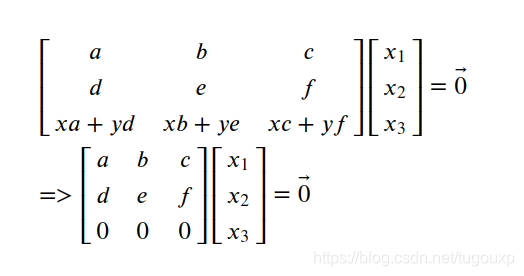
让x3为自由变量:

所有由此可见,行向量线性相关必定导致有列向量标识的方程组有非零解,所有列向量也必然线性相关。
相关性和线性方程组之间的关系很微妙,如果行向量线性相关,则必定可以通过行变换消去一个方程,消去方程会导致自由变量多一个,则剩余的方程必定有非零解,有非零解同时也意味着列向量必定线性相关。。。
对于通用情况:
设以下mxn矩阵,其中m<n。

将其写成列向量的格式:

假设其列秩为c,则必定存在c个列向量线性无关.我们将其挑选出来做成新的矩阵

其中
 (j<n)
(j<n)
则原矩阵
![]() 必定可以写成
必定可以写成

线性组合的形式:


同时,也可以写成B矩阵行向量线性组合的形式:

其中

另一种证明:
考虑矩阵,
为一
阶矩阵,设它的行秩为
,列秩为
.
考虑一下 的解空间,则
的行阶梯型
将有
个首1元素行,必定有
个自由变量,所以A的解空间的维数必为
.
另外,考虑到
所以
和
是互为正交补空间,
的秩为
所以
QED!
初中时老师告诉我们,有n个方程才能唯一确定n个未知数,所以才叫"方“程,可是现在我们知道了,光有n个方程还不够,这些方程必须是”干货“方程才行。
4.矩阵线性组合的把戏:


以上说明,如果现行线性相关的航向量作为最后一行参与列扩张,扩张成的列向量,满足同样的行扩张系数。
5.最小二乘法的矩阵形式推导:
设:
最小二乘问题的矩阵形式:
求得向量,使得
与
的距离最小,翻译成数学表达就是:
,求
,使得
最小,2-范数表示的是向量长度,计算方法是向量各个元素的平方和再开方,求它最小值,等价于求:
的最小值,而:
根据矩阵微分公式:
所以:
所以,最终得到:
对于方阵来说,它和
同解
QED!
数形结合的方法不一定到处可用,经济学中的数学模型通常有上千个变量,比如说
这样就意味着必须在中工作,这样的空间不能通过几何手段来处理,但是代数方法却可以很好的发挥作用,因此这门学科叫做线性代数。
6.是不是
上的子空间.
1.显然 ,满足
,所以存在加法单位元
2.,则
所以,满足加法封闭性.
3.,
满足标量乘法的封闭。
所以,是子空间
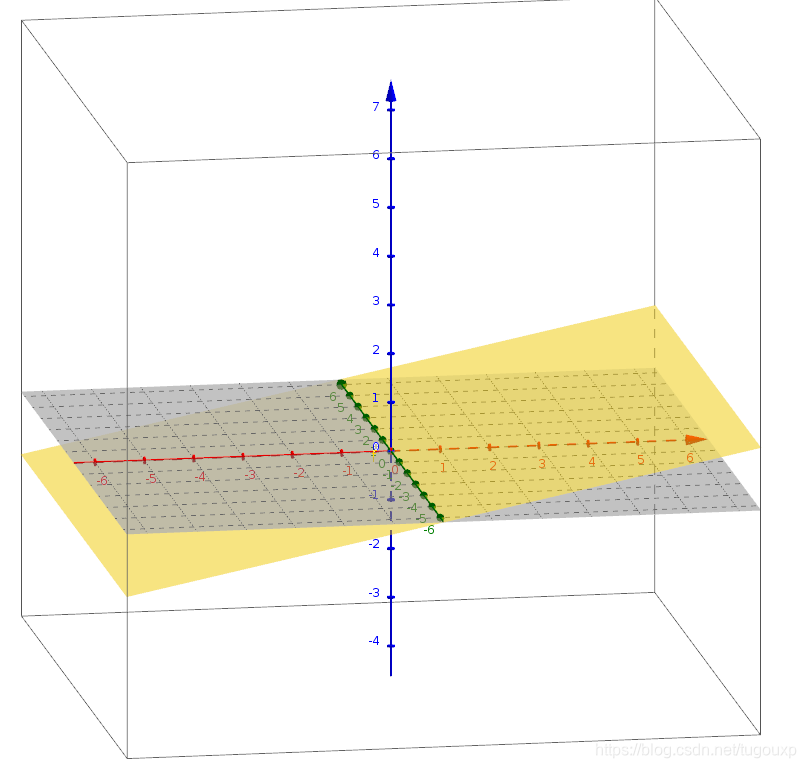
空间图形如下图所示:
是个过原点的二维空间。
可以想象,不过原点的二维空间是什么样子的?在这个空间中的生物,可能走一小步,就跳出了这个空间,
7:设
张成V,证明组
也张成V
满秩,所以存在逆矩阵,所以
所以,得证明!
或者
也就是线性无关,线性无关的一组向量可以作为
的一组基,所以得证!
以上就是两种方法的证明!
8若将C视为R上的向量空间,则组 是线性无关的。
若将C视为C上的向量空间,则组是线性相关的。
则
在R上,b=d=0
所以
在C上
两个方程,四个未知数,解空间是二维平面,所以有无穷多个解,例如.
a=d=0, b=c=1
得到
结束!
9:
是区间[0,1]上的连续函数。
证明
假如存在
使得:
根据如下函数图形,当x取的时候
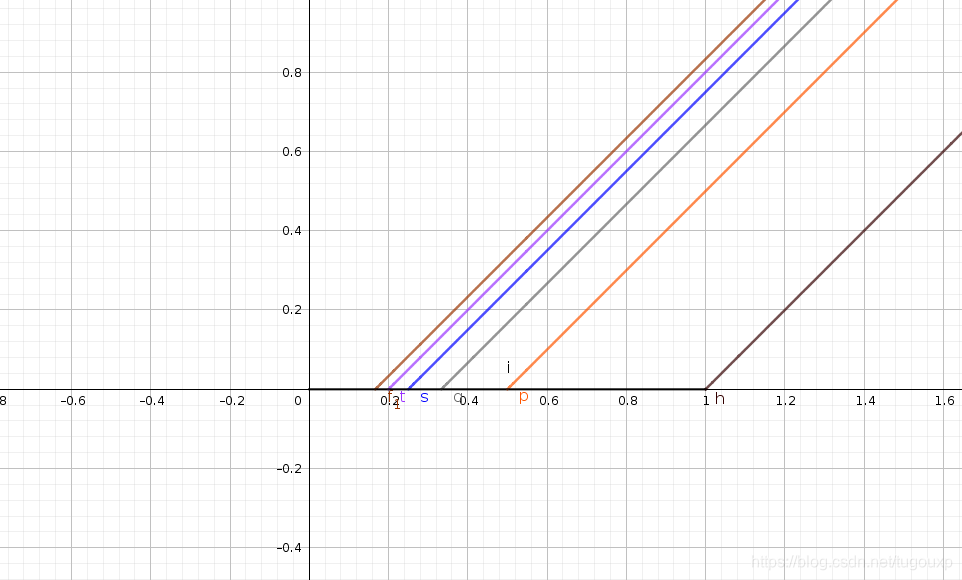
但是
所以,显然,不存在n+1次的函数能够用<=n次的函数表达的情况,函数无关。
9:对于线性变换 ,计算他在新坐标基B下的变换矩阵。
所以:
所以:
所以新基下的变换为:
10:内积的定义:
对于任何
,可以将其单位化:
11:转置矩阵和原矩阵具有相同的特征多项式,也就是具有相同的特征值.
12:向量刻画对象,矩阵刻画对象的运动,矩阵的本质是对运动的描述,线性空间中的跃迁,交换.
运动的方式*对象=运动后的对象
12:利用范德蒙德行列式证明,属于不同特征值的特征向量线性无关:
课本上用数学归纳法,不太喜欢反证法和归纳法,还是用演绎法来证明:
假设n阶梯矩阵A有n个不同的特征值,分别为:
其对应的特征向量分别为:
证明:使得成立的只能是
证明过程:根据已知条件下式成立:
并且:
如果成立,那么下面的式一定成立:
等价于:
转化成矩阵形式:
也就是
其中:
是范德蒙德行列式,其行列式的值为:
引用特征向量各不相同的条件,则此范德蒙德行列式一定不等于0.得出此范德蒙德矩阵是满秩矩阵.
满秩矩阵就一定有唯一的逆,所以
由于作为特征向量,特征向量表示方向,不可能为0, 那么
只能是,得证.
还可以认为,矩阵:
的解空间的秩为n,根据维数定理,解空间的秩+矩阵的秩=n,则矩阵的秩一定为0.
什么样的矩阵秩才为0呢?当然是0矩阵,根据上面的逻辑,同理得出,
所以属于不同特征值的特征向量线性无关.
QED!
12:与
相似,则
,那么
与
有什么关系?
因为
所以 与
相似
13:实对称矩阵的特征值为实数
复数为实对称矩阵
的特征值,复向量
为对应的特征向量,即:
用表示
的共轭复数,
表示
的共轭复向量.那么
从上式也可以得出,如果结论为真,那么也为A的特征向量.
于是有:
和
让两式相减:
由于
所以,
所以
也就是
即,特征值为实数.
由于实对称矩阵的特征值是实数,所以,齐次线性方程组
是实系数线性方程组,又由于
得到
,所以其必有非平凡实数解,必有实的基础解系.所以,实对称矩阵不但特征值是实数,对应的特征向量也是实向量.
14:设是实对称矩阵的两个特征值,
是对应的特征向量,若
,则
与
正交.
已知条件,,
所以:
于是:
所以:
由于,所以只能是
成立,也即是
正交.
15:若是一组n维标准正交向量组,求矩阵
的所有特征值.
标准正交,所以:
展开:
则:
根据正交条件,交叉项全部为0,
所以
也就是
所以,特征多项式为:
也就是特征值为或者
验证:
所以,M的每个列向量都是的特征向量。
同理:
所以,M-E的每个列向量都是0的特征向量。
16:对于阶可逆矩阵
,设其任意一个非零特征值
,对应的特征向量
,则
连边同时左乘
然后两边乘以,得到:
也就是:
所以,是
的特征值,对应特征向量不变,仍然为
.
特征向量不为, 所以,对于0特征值的情况
所以,齐次方程
有非0解,进而得到 Rank(A)<n,得到
17: 为
阶正定矩阵,则
正定矩阵,A是对称方阵,则,写成分块的形式:
对矩阵尽心给出等列变换,用第二列减去第一列右乘以,行列式不变,所以:
也就是:
根据已知矩阵正定的条件,一个矩阵是正定的,当且仅当它的各阶顺序主子式是正定的,所以必然也是正定的。
根据正定矩阵的要求,
所以
所以得到:
同理,可以得到
所以
得证!
18.若P为正交矩阵,则线性变换
称为正交变换
则
由于 2-范数表示向量长度,所以,
说明经过正交变换后,线段长度保持不变,从而几何形状保持不变,这是正交变换的特性.
19:设和
是方阵A的两个不同特征值,
和
分别对应于
和
的线性无关特征向量,则
线性无关.
题设可知:
假设
两边同时乘以得:
得:
所以
由于,所以
因为线性无关,所以
从而式可以化简为
同样因为线性无关.
根据 得到:
所以,线性无关结论成立.
20:
如果
则:
21:证明对称矩阵为正定的充分必要条件是:存在可逆矩阵
,使得
,也就是A与单位矩阵E合同.
充分性:
对称且正定,则存在正交矩阵
,使得
设矩阵是对角矩阵
对角元的平方根的对角阵,则:
所以,
另
,由于P,C均为可逆阵,所以U必为可逆阵.
得到
必要性:
所以,必正定.
QED!
22:
的
元为:
则:
是自然数
的一个排列.
代数证明卡壳了,先写到这里,后面想到在补充.下面换另一个思路证明:
对于任一初等矩阵
如果 奇异,则
如果B非奇异,则
23:
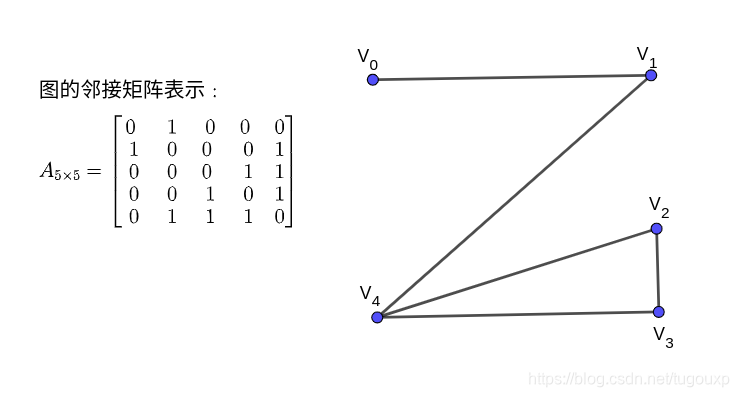

为某图的
邻接矩阵,且
表示的
元素,则
等于顶点
和
间长度为
的路的条数
证明:利用数学归纳法,时,由邻接矩阵定义得知,
表示从顶点
到
长度为1的路的数量,假设对某个
,矩阵
中的每一元素表示相应两顶点间长度为
的路的数量,因此,
表示从顶点
到
长度为
的路的数量,如果有一条边
,则
表示从顶点到
长度为
的形如:
的路的数量,另一方面,如果不是一条边,则从
到
没有长度为
的路,并且
所以,可以得到,从到
长度为
的所有路的总数为:
而恰好是的
元素.
24:设阶矩阵
的特征值为
,证明:
证明:
为
的特征多项式,则:
按照第一列进行展开,可以得到:
将按照同样的方式展开:
其中 不包括两个对焦元素
和
,更徨论其余的子式了.
所以,的展开式式中唯一包含多于
个对角元素的项,一定是
同时
对照两个式子的系数,得到
另,根据跟与系数的关系,可得:
QED!
25:cramer法则的证明:
如果:
所以
矩阵的伴随矩阵为:
将前式乘以伴随矩阵
也就是:
所以:
26:另
及
为一个向量空间
的两个有序基,并令
为
上的线性算子,令
为从
到
的转移表示矩阵.
设
为向量 在
世界中的坐标
则转换成标准坐标系下表示的坐标为:
经过变换后,坐标变为:
所以,是
世界的坐标,变为标准坐标系:
所以:
所以,从 世界的角度看
,
的坐标分别为
所以
所以是从E到F的转移矩阵.
或者,已知
因此,若
,
则
于是
27:若和
为
或者
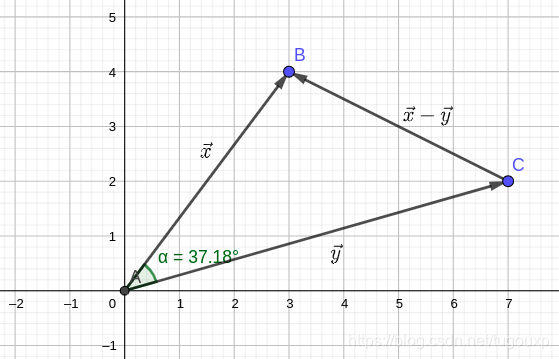
中的两个非零向量,且
为它们之间的夹角,则:
证明过程:
由余弦定理,我们有:
得到:
QED!
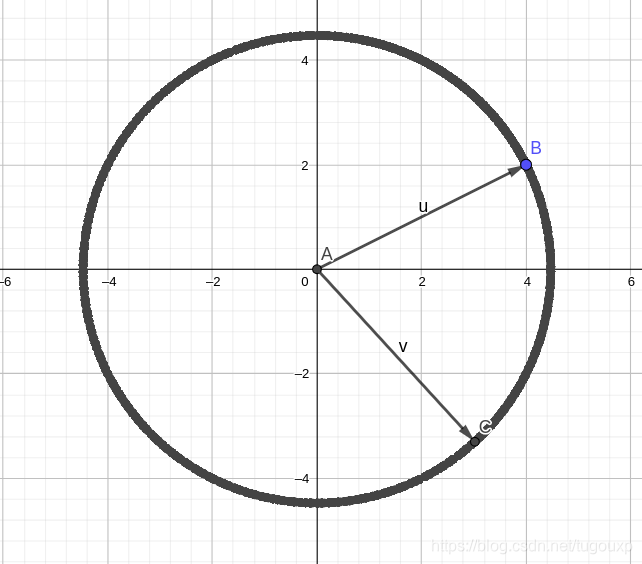
28:旋转矩阵
如果,则
所以,对于下向量,经过正交变换后,长度不变
28:
在上定义内积,
,
集合
为一个正交向量集合,因为,对任意的正整数和
是单位向量,因为:
为了构造一个规范正交基,只要在1的方向上构造单位向量.
所以,
为一个规范正交的向量集合.
根据以上信息,不求原函数,计算
计算过程:
因为
所以可以表示为正交坐标系中坐标为
的点.
分析:
29:假设在标准坐标系下的正交向量
以及
则
则加入存在新的基,从
到标准坐标系的转移矩阵是
则新的的内积是?
所以,
当为正交变换时,
所以,
反之,如果A并非正交变换,则结果
内积不一定为0!
同样道理,内积为0,不表示这两个向量一定正交垂直,还要看它的坐标系.
比如,二维平面连个无关向量,,其中
,则以他们为基的坐标点
和
虽然内积为0,但他们并不垂直.
大致可以得到一个结论,要准确描述向量,首先要确定一组基,然后给出在基所在的各个直线上的投影值,就可以了。为了方便求坐标,我们希望这组基向量模长为 1。因为向量的内积运算,当模长为 1 时,内积可以直接表示投影。然后还需要这组基是线性无关的,我们一般用正交基,非正交的基也是可以的,不过正交基有较好的性质。
30:正交矩阵的特征值有什么规律?
假设是正交矩阵,则
特征值为,对应特征向量
则
两边转置
同时右乘
所以,阶正交矩阵一定相似于
意味着
由于实对称矩阵的特征值是实数,不失一般性,假设是1,所以,齐次线性方程组
是实系数线性方程组,又由于
得到
, 所以其必有非平凡实数解,也就是必有实的基础解系.正交矩阵不但有着实的特征值,其特征向量也是实的。
这个结论有什么意义呢?从这个结论 可以得出,在三维空间中的刚体变换,一定存在一个对称轴,在对称轴方向上,刚体的尺度不发生变化。
31:
为一
实矩阵,它有一个复特征值
,并令
为属于
的一个特征向量,向量
可以分解为实部和虚部.
由于的元素均为实的,可得
也是
的一个特征值,它相应的特征向量为:
且和
均为一阶方程组
的解,这两个解的任意线性组合也将是一个解,
因此,令
所以:
32:证明和
具有相同的非零特征值
是一个
的矩阵
因为,所以
的解同样为
的解。
因为
,所以的解同样也是
的解,所以在
空间中,它们具有相同的零空间,所以
同样道理,
所以:
下面证明,特征值相同:
设是
的特征值
对应的特征向量
实际上有一个更强的结论,两个矩阵应该是相似的。
QED!
33:
其中
所以
形式上的确如此,证明一下:
设中的元素
则
34.如果当,必有
,则
是单的,也叫“一对一”的映射。
比如,对于
其中
所以实际上是一个
的矩阵,而
是单的等价于方程组
有唯一解.
如果,则表示方程数目大于未知量的数目,相当于从低维空间映射到高维空间,则在系数无关的情况下必定有唯一解或者无解,所以,可能是单的。
但如果,则表示方程数目小于未知量数目,相当于从高维空间映射到低维空间,必然有多个非零解,所以,不可能是单的。
例如,对于映射:
他是将二维坐标映射到三维坐标,是升维度映射,所以是单射,从下图可以看到,左边二维空间映射为右边三维空间的二维子空间,映射后的空间构成一个平面,仍然是二维的。

对偶空间:
是的线性映射,
是
空间,
是
空间。
则:
的基是
的基是
所以,对于的映射
35.设A为阶对称矩阵,
是A的特征方程的r重根,则矩阵
的秩
,从而对应特征值
恰好有r线性无关的特征向量.