时间复杂度和空间复杂度基础

时间复杂度

时间复杂度有好多种定义方式，什么big O，small o，big Omega，small omega，balabala，首先先了解几个概念：
$T(n)$是Every-case time complexity，就是用来定义一个算法对于大小为$n$的对象所做的运算次数。
有$T(n)$就还有$W(n)$，W代表worst；$B(n)$，B代表best；$A(n)$，A代表average等等。

Big O

着重介绍以下Big O的定义，和如何用定义证明例子

定义

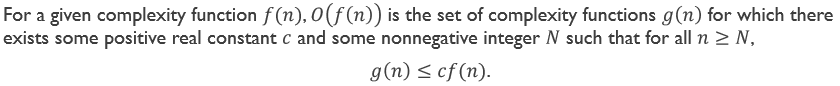
看起来很绕口，其实关键点就是$cf(n)$是一个上限，$c$是个正的常数，$n$也是个大于等于某个非负数$N$的常数。

例子

一、证明$n^2+10n\in O(n^2)$
$$n^2+10n\le n^2+10n^2=11n^2$$
通过上面的定义，$c=11,N=1$，我们就证明了$n^2+10n\in O(n^2)$
二、判断$2^{2n}\in O(2^n)$对不对
$$2^{2n}=2^n{2}^n\le c{2}^n{2}^n\le c$$
我们得找一个正常数$c$，但这里$n$不确定，所以就找不到啦。因此，通过定义证明了$2^{2n}\in O(2^n)$是错的（其实一眼就看得出来是属于$O(4^n)$）。当题目比较复杂时，我们也可以将式子转换为求极限再借助洛必达法则来求解。
$$li{m}_{n\to \infty }\frac{g(n)}{f(n)}=\{\begin{array}{r}cimpliesg(n)\in \Theta (f(n))ifc>0\\ 0impliesg(n)\in o(f(n))\\ zimpliesg(n)\in \omega (f(n))\end{array}$$

其他

Big O是最常用的，还有其他的一些定义比如big Omega ($\Omega (n)$), big Theta ($\Theta (n)$), small o($o(n)$), small omega ($\omega (n)$)等等。我们就用下面的这个例子大概讲一讲他们的关系，这样可以更好的理解。

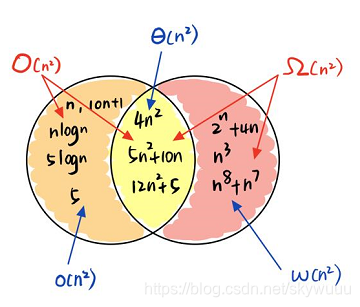
上面的图片中括号内的$n^2$其实就是f(n)，然后将下列$O(n),\Omega (n),\Theta (n),o(n),\omega (n)$分别代入上面big O的定义来看，就可以很好的理解了。
$O(n):g(n)\le cf(n)$（存在c (exsit some positive real constant $c$)）
$\Omega (n):g(n)\ge cf(n)$（存在c）
$\Theta (n):cf(n)\le g(n)\le df(n)$ （也就是$\Theta (f(n))=O(f(n))\cap \Omega (f(n))$）（存在c）
$o(n):g(n)\le cf(n)$（任意c (every positive real constant $c$)）
$\omega (n):g(n)\ge cf(n)$（任意c）

两大法则

那么如何用判断一段代码的时间复杂度（一般指big O）呢？这里有三大法则。

1. 除了执行最多次的代码，别的统统忽略

例如：

void func(int n){
	int a = 0;
	int b = 1;
	for(int i = 0; i < n; i++){
		a += i;
		b += a;
	}
	for(int i = 0; i < n; i++){
		for(int j = 0; j < n; j++){
			cout << a;
		}
		cout << b << endl;
	}
}

这段代码很明显就可以看出两个for loop执行的代码次数最多，所以只关注它即可。这里也就是$O(n^2)$。

2. 有嵌套的，就把它们乘起来

例如：

void for_loop(int a, int n){
	for(int j = 0; j < n; j++){
		cout << a;
	}
}
void func(int n){
	int a = 0;
	int b = 1;
	for(int i = 0; i < n; i++){
		a += i;
		b += a;
	}
	for(int i = 0; i < n; i++){
		for_loop(a, n);
		cout << b << endl;
	}
}

先用法则二将for_loop函数替换成上面的代码，其实和上面的例子一样，都是两个for loop，这时候只需要将他们的乘起来，也就是$n\times n=n^2$，就能得到答案$O(n^2)$了。有一种整体法的数学思想在里面。

特殊例子

O(logn)是什么？

例如：

int sum = 1;
for(int i = 1; i <= n; i++){
	i *= 3
	sum += i
}
cout << sum << endl;

此段代码中，变量$i$每次都是上次的3倍（3, 9 , 27…），假设执行次数为$x$，我们可以列出这个等式$3^x=n$，化简得到$x=lo{g}_{3}n$，我们一般都习惯用2为底的对数来表示，所以进一步化简得$x=lo{g}_{3}2\cdot lo{g}_{2}n$，总执行步骤次数就是$O(logn)$了。

空间复杂度

空间复杂度远没有时间复杂度难算。计算空间复杂度只需要计算总的分配空间就可以了。
例如：

int* create_arr(int n){
	int* arr = new int[n];
	return arr;
}

此段代码就分配了$n$大小的空间。

参考

1. 两年前自己整理的笔记和老师的课件
2. 《数据结构与算法分析——C语言描述》