上一节我们分析了二阶有源低通滤波器,这一节我们来继续,分析其他种类的二阶滤波器,包括高通、带通、带阻滤波器。
由于分析过程是类似的,都是以节点列方程,化简后得到传递函数,本篇就不具体写计算过程了,直接给出仿真图和传递函数的结果。
1)二阶有源高通滤波器
二阶有源高通滤波器的电路,可以简单地将二阶低通滤波器中的R和C位置互换,就可以得到。
仿真图如下:

仍然选择R1 = R2 = R,C1 = C2 = C,则其传递函数为:
,其中
,
从传递函数的表达式中也可以看出,当 s 很小时,的值也很小;当s值增大,则
也会增大;当s接近于无穷时,
约为
;所以为高通滤波器。
仿真图中,可以看到波特图低频区间增益很小,高频区间增益为近似定值。(图中频率特别高时,增益有下降是因为运放的带宽有限,极高频率下会衰减;所以,选用运放时要选择带宽足够能通过所有的有效信号)
2)二阶有源带通滤波器
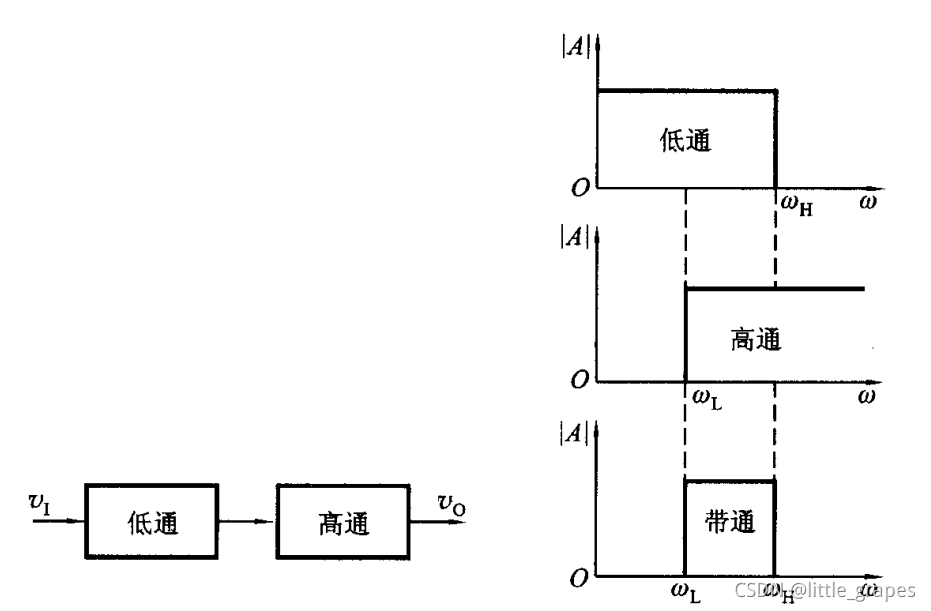
带通滤波器可以简单由低通滤波器和高通滤波器串联得到,如果低通滤波器的截止频率比高通滤波器的截止频率高,那么,处于中间频段的信号就可以通过。
典型的二阶有源带通滤波器如下图:
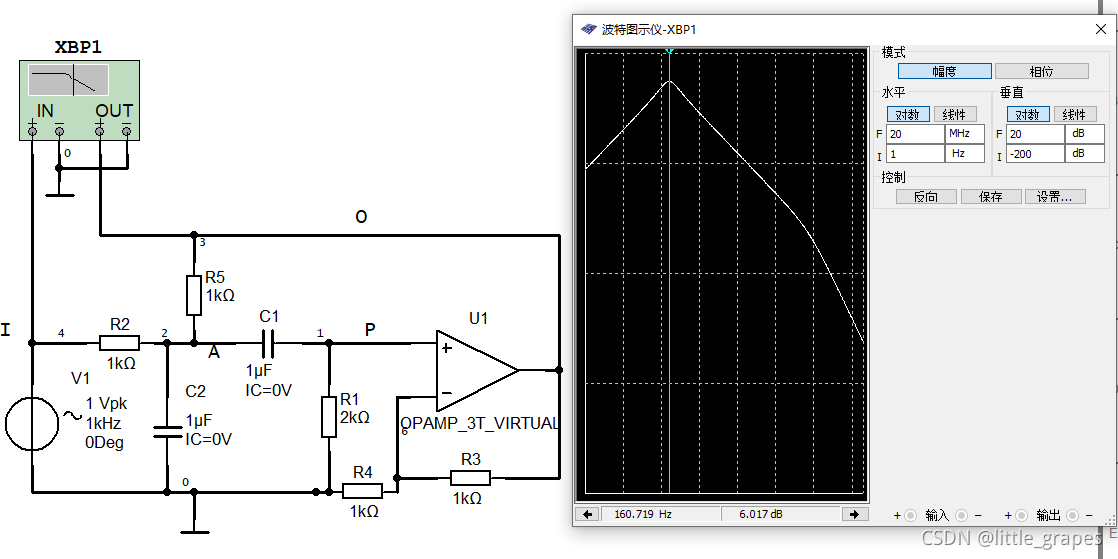
这里选择R1 = 2*R2,R2 = R5。可以计算得到:
令,
,
,则可以转换为:
当 ω = ω0 时,有最大增益,即该带通滤波器的通带中心频率为ω0 。
而其通带宽度与Q有关,Q越大,带宽越小。带宽为:BW = ω0/2πQ。
如下图显示的是Q值变大后的仿真图,可以看到通带的不同:
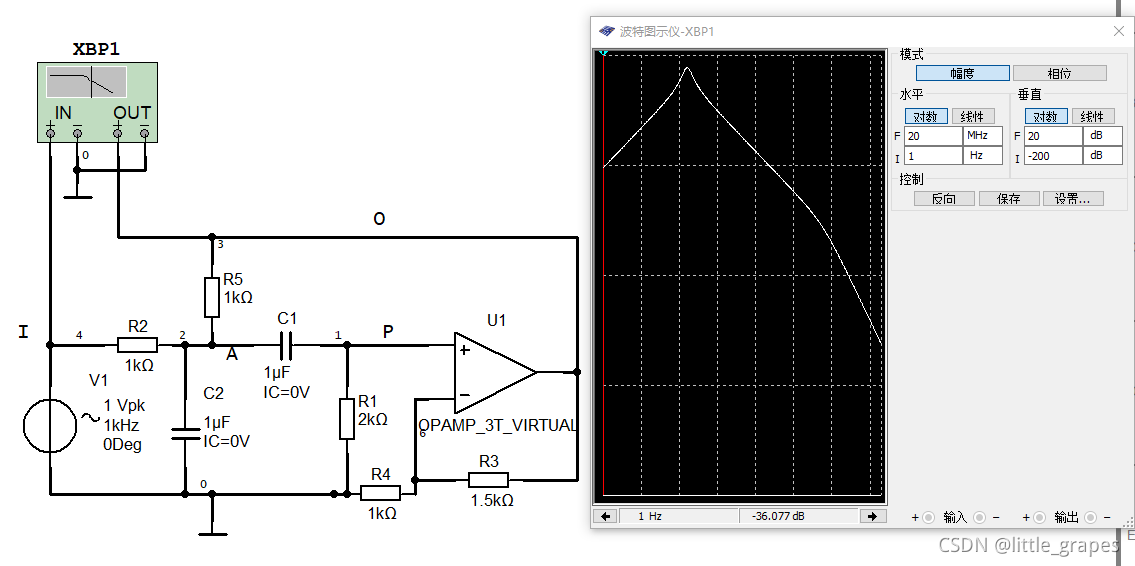
3)二阶有源带阻滤波器
与带通滤波器一样,带阻滤波器可以通过高通和低通并联而成。只要低通滤波器的截止频率低于高通滤波器的截止频率,那么处于低频和高频的信号可以通过,中间频段的信号会被衰减,即实现了带通滤波器的作用。
但是,一般更常见的电路形式是双T带阻滤波器,仿真见下图:

传递函数为:
其中是该带阻滤波器的中心角频率;
为增益;
。
Q越大,则带阻滤波器的选频特性越好。下图是将Q值减小之后得仿真图,可见阻带带宽增加了。
