多传感器融合定位四-3D激光里程计其四：点云线面特征提取

Reference:

1. 深蓝学院-多传感器融合
2. 多传感器融合定位理论基础
3. LOAM论文和程序代码的解读

文章跳转：

1. 多传感器融合定位一-3D激光里程计其一：ICP
2. 多传感器融合定位二-3D激光里程计其二：NDT
3. 多传感器融合定位三-3D激光里程计其三：点云畸变补偿
4. 多传感器融合定位四-3D激光里程计其四：点云线面特征提取
5. 多传感器融合定位五-点云地图构建及定位
6. 多传感器融合定位六-惯性导航原理及误差分析
7. 多传感器融合定位七-惯性导航解算及误差分析其一
8. 多传感器融合定位八-惯性导航解算及误差分析其二
9. 多传感器融合定位九-基于滤波的融合方法Ⅰ其一
10. 多传感器融合定位十-基于滤波的融合方法Ⅰ其二
11. 多传感器融合定位十一-基于滤波的融合方法Ⅱ
12. 多传感器融合定位十二-基于图优化的建图方法其一
13. 多传感器融合定位十三-基于图优化的建图方法其二
14. 多传感器融合定位十四-基于图优化的定位方法
15. 多传感器融合定位十五-多传感器时空标定(综述)

1. 点云线面特征提取

1.1 按线数分割

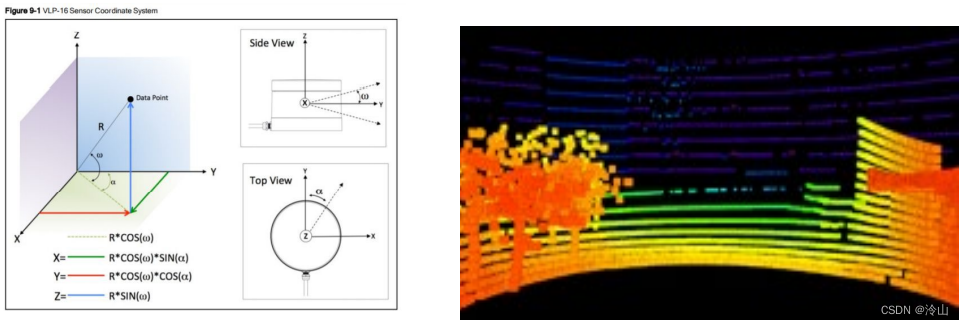
根据激光点坐标，可计算该束激光相比于雷达水平面的倾角 $\omega =\arctan \frac{z}{\sqrt{x^2+y^2}}$
根据倾角和雷达内参(各扫描线的设计倾角)，可知雷达属于哪条激光束。

1.2 计算曲率（重要！）

根据前后各5个点与当前点的长度(长度指激光点到雷达的距离)(应该是在同一线下的前后5个点)，计算曲率大小(下面公式为LOAM代码中的实现方式，并不是传统意义上的曲率)：
$$c=\frac{1}{\Vert X\Vert }\Vert \sum _i\left(X-X_i\right)\Vert$$(这里面的$\sum$是在范数内，没有问题)该计算方式很明显的体现了这个平面是否平的信息。

像这种在墙角的情况下，虽然在 $x$ 方向上很小，但是在 $y$ 方向很大。($c=d{x}^2+d{y}^2+d{z}^2$)

1.3 按曲率大小筛选特征点

一个面上的曲率肯定是小的，而一个线特征的曲率肯定是大的，那么反过来讲，可以通过曲率大小来划分线特征还是面特征。(这里不理解可以看下面的图)

线特征和面特征内部的曲率还应该做一些差异上的区别。假如我们求一个点到线的距离的时候，假如这个线上有一百个点，不可能这一百个点都求一个点到线的距离，这个计算量会大到无法接受，这时只能选一部分点来计算点到直线的距离。应该将曲率最大的几个点选出来-----曲率大的点有更大的概率属于一个良好的线特征(错误归进来的点可能并不属于线特征，它们的曲率一般都是比较小的)，反之亦然。这样就不会影响求取残差时的结果了。

共分4类：
a. 曲率特别大的点(sharp)
b. 曲率大的点(less_sharp)
c. 曲率特别小的点(flat)
d. 曲率小的点(less_flat)

实际使用时：
a. sharp 为“点到直线”中的“点”（当前帧）
b. sharp 和 less_sharp 为 “点到直线”中的直线（上一帧）
c. flat 为“点到平面”中的“点”（当前帧）
d. flat 和 less flat 为 “点到平面”中的“平面”（上一帧）

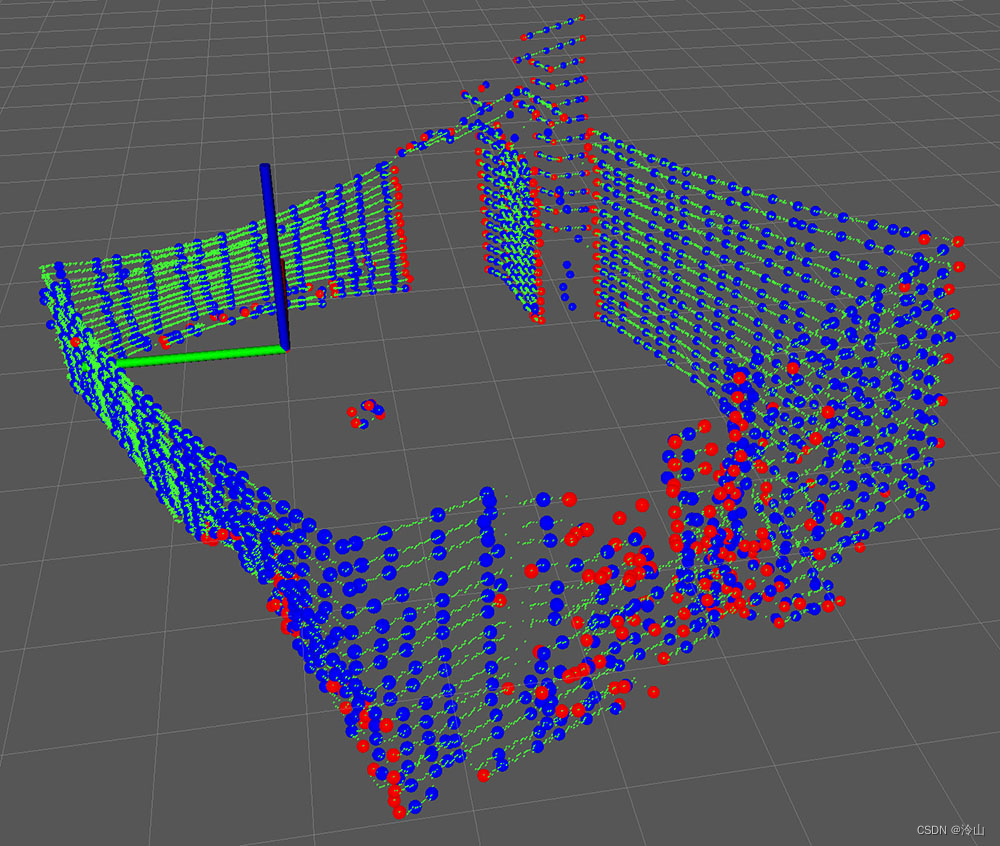
如下图所示，绿色点为velodyne 16线激光雷达的原始点云，扫描环境是卧室，大概就是一个长方体，能够看到点云在垂直方向大致分成了16条线。红色的小圆球是提取出来的角点(曲率特别大的点)，蓝色的是平面点。可见，角点基本上位于房间的墙角和过渡较大的地方，例如物体（窗帘）的边缘。

接下来对特征点分的更细一些，除了角点和平面点，还使用了曲率 $c$ 不太大的点（称为less sharp point），和曲率不太小的点（称为less flat point），下图中红色的小圆就是less sharp point，蓝色的小圆是less flat point。在右侧的图中我把门打开了，可以清晰地看到门口边界有更多的less sharp point。

2. 基于线面特征的位姿变化

现在介绍一下，在得到线面特征之后，怎么进行位姿优化。

假设有两帧 $k$ 帧和 $k+1$ 帧，两个里面都有线面特征，两帧之间理论上是有很多线是对应的，也就是说，在 $k$ 帧和 $k+1$ 帧的线，有些打在了同样的物体上，这样属于同一个线/面，就可以做关联了。如果 $k$ 帧和 $k+1$ 帧的线不重合，那肯定就是位姿和误差导致的。也就是说，我们可以通过线/面是否重合，来反推出第 $k+1$ 帧相对于第 $k$ 帧是什么样子的，这就是我们想要的里程计了。

2.1 帧间关联

2.1.1 点云位姿转换

第 $k+1$ 帧与第 $k$ 帧的相对位姿为：$T=\left[\begin{array}{ll}R& t\\ 0& 1\end{array}\right]$

$k+1$ 帧中的点 $p_i$ 转到第 $k$ 帧坐标系：${\tilde{p}}_i=R{p}_i+t$

这里可以先使用第 $k$ 帧与第 $k-1$ 帧的相对位姿，先猜测一个第 $k+1$ 帧与第 $k$ 帧的相对位姿的近似值。

2.1.2 线特征关联

当 $p_i$ 为 sharp 时(用曲率大的点)，在上一帧中搜索离 ${\tilde{p}}_i$ 最近的线特征点，并在相邻线上再找一个线特征点(距离 ${\tilde{p}}_i$ 最近)，组成直线。这时用 $k+1$ 上的一个点，在第 $k$ 帧中，找到了这个线特征对应的线，有了点和线，就可以求点到直线的距离了。

2.1.3 面特征关联

当 $p_i$ 为 flat 时，在上一帧中搜索离 ${\tilde{p}}_i$ 最近的面特征点，并在相邻线上找两个面特征点，组成平面。(同一个线上找一个，相邻线上再找一个，三个点构成一个面)

2.2 残差函数

2.2.1 线特征

点到直线的距离：
$$d_{\mathcal{E}}=\frac{\left|\left({\tilde{p}}_i-p_b\right)\times \left({\tilde{p}}_i-p_a\right)\right|}{\left|p_a-p_b\right|}$$在实际代码中，使用的是矢量形式，而不是直接取模，其实在求残差函数时，都是求的$f^{T}f$，区别不大：
$$d_{\mathcal{E}}=\frac{\left({\tilde{p}}_i-p_b\right)\times \left({\tilde{p}}_i-p_a\right)}{\left|p_a-p_b\right|}$$

2.2.2 面特征

点到平面的距离：
$$d_{\mathcal{H}}=\left({\tilde{p}}_i-p_j\right)\bullet \frac{\left(p_l-p_j\right)\times \left(p_m-p_j\right)}{\left|\left(p_l-p_j\right)\times \left(p_m-p_j\right)\right|}$$

2.3 位姿优化

根据非线性优化理论，只要求得残差关于待求变量的雅可比，便可采用高斯牛顿等进行优化。

2.3.1 线特征残差雅可比

$$J_{\epsilon }=\frac{\partial d_{\epsilon }}{\partial T}=\frac{\partial d_{\epsilon }}{\partial {\tilde{p}}_i}\frac{\partial {\tilde{p}}_i}{\partial T}$$ $\partial d_{\epsilon }$ 是残差，针对残差求导。$\frac{\partial d_{\epsilon }}{\partial T}$ 直接求导比较复杂，所以采用了链式求导法则。

等号右边第二项 $\frac{\partial {\tilde{p}}_i}{\partial T}$ 与李代数相关，此处直接给出结论，推导过程见《视觉SLAM十四讲》第 $4.3$ 节。
对平移的雅可比：$\frac{\partial {\tilde{p}}_i}{\partial t}=I$
对旋转的雅可比：$\frac{\partial {\tilde{p}}_i}{\partial R}=-{\left(R{p}_i+t\right)}^{\wedge }$

等号右边第一项 $\frac{\partial d_{\epsilon }}{\partial {\tilde{p}}_i}$ 可以根据外积的微分性质，推导得到：
$$\begin{array}{rl}\frac{\partial d_{\epsilon }}{\partial {\tilde{p}}_i}& =\frac{1}{\left|p_a-p_b\right|}\left(\frac{\partial {\left({\tilde{p}}_i-p_b\right)}^{\wedge }\left({\tilde{p}}_i-p_a\right)}{\partial {\tilde{p}}_i}+\frac{{\left({\tilde{p}}_i-p_b\right)}^{\wedge }\partial \left({\tilde{p}}_i-p_a\right)}{\partial {\tilde{p}}_i}\right)\\ & =\frac{1}{\left|p_a-p_b\right|}\left(-{\left({\tilde{p}}_i-p_a\right)}^{\wedge }+{\left({\tilde{p}}_i-p_b\right)}^{\wedge }\right)\\ & =\frac{{\left(p_a-p_b\right)}^{\wedge }}{\left|p_a-p_b\right|}\end{array}$$该式推导过程：

1. 线特征点到直线距离：$d_{\mathcal{E}}=\frac{\left({\tilde{p}}_i-p_b\right)\times \left({\tilde{p}}_i-p_a\right)}{|p_a-p_b|}$，上面可以变成 ${\left({\tilde{p}}_i-p_b\right)}^{\wedge }\left({\tilde{p}}_i-p_a\right)$
2. 偏导有性质：$\frac{\partial x_1{x}_2}{\partial y}=\frac{\partial x_1}{\partial y}\cdot x_2+x_1\cdot \frac{\partial x_2}{\partial y}$
3. $\partial {\left({\tilde{p}}_i-p_b\right)}^{\wedge }\left({\tilde{p}}_i-p_a\right)$ 内 $\partial {\left({\tilde{p}}_i-p_b\right)}^{\wedge }$是个矩阵不好求偏导，这时使用另一个性质：$a^{\wedge }b=-b^{\wedge }a$ 又可推导出 $\frac{\partial a^{\wedge }b}{\partial a}=-\frac{\partial b^{\wedge }a}{\partial a}=-b^{\wedge }$
4. $-{\left({\tilde{p}}_i-p_a\right)}^{\wedge }+{\left({\tilde{p}}_i-p_b\right)}^{\wedge }$ 是矩阵，可以相互加减，抵消掉了 ${\tilde{p}}_i$，得到最终公式

2.3.2 面特征残差雅可比

$$J_{\mathcal{H}}=\frac{\partial d_{\mathcal{H}}}{\partial T}=\frac{\partial d_{\mathcal{H}}}{\partial {\tilde{p}}_i}\frac{\partial {\tilde{p}}_i}{\partial T}$$等号右边第二项与线特征的一致。
残差函数为：
$$d_{\mathcal{H}}=|\left({\tilde{p}}_i-p_j\right)\bullet \frac{\left(p_l-p_j\right)\times \left(p_m-p_j\right)}{\left|\left(p_l-p_j\right)\times \left(p_m-p_j\right)\right|}|$$若令
$$X=\left({\tilde{p}}_i-p_j\right)\bullet \frac{\left(p_t-p_j\right)\times \left(p_m-p_j\right)}{\left|\left(p_t-p_j\right)\times \left(p_m-p_j\right)\right|}$$则有
$$\frac{\partial d_{\mathcal{H}}}{\partial {\tilde{p}}_i}=\frac{\partial |X|}{\partial {\tilde{p}}_i}=\frac{\partial |X|}{\partial X}\frac{\partial X}{\partial {\tilde{p}}_i}=\frac{X}{|X|}\frac{\partial X}{\partial {\tilde{p}}_i}$$关于$\frac{\partial |X|}{\partial X}$是怎么得到$\frac{X}{|X|}$的，假设$a=(x,y,z)$，那么$\frac{\partial |a|}{\partial a}=\frac{\partial \sqrt{x^2+y^2+z^2}}{\partial (x,y,z)}=\frac{(x,y,z)}{\sqrt{x^2+y^2+z^2}}=\frac{a}{|a|}$

对于等号右边第二项，根据内积的微分性质，有
$$\frac{\partial X}{\partial {\tilde{p}}_i}=\frac{\left(p_l-p_j\right)\times \left(p_m-p_j\right)}{\left|\left(p_l-p_j\right)\times \left(p_m-p_j\right)\right|}$$物理意义上，它代表的是平面的单位法向量。

3. 位姿代码实现

3.1 ceres 基础知识

3.1.1 基本概念

优化任务一般可以表示成如下形式：
$$\begin{array}{rl}& \underset{\mathbf{x}}{\min }\frac{1}{2}\sum _i{\rho }_i\left({\Vert f_i\left(x_{i_1},\dots ,x_{i_k}\right)\Vert }^2\right)\\ & \text{ s.t. }{l}_j\le x_j\le u_j\end{array}$$其中，

1. ${\rho }_i\left({\Vert f_i\left(x_{i_1},\dots ,x_{i_k}\right)\Vert }^2\right)$ 称为残差块，即 ResidualBlock；
2. $f_i(\cdot )$ 称为代价函数，对应之前讲的残差函数，即 CostFunction；
3. $\left[x_{i_1},\dots ,x_{i_k}\right]$ 这一系列参数称为参数块（待优化参数），即 ParameterBlock；
4. ${\rho }_i(\cdot )$ 称为损失函数，即 LossFunction，对应之前的大F。（应该是 ${\min }_{\mathbf{x}}\frac{1}{2}{\sum }_i{\rho }_i(\cdot )$ 才对吧）

残差块ResidualBlock包含了代价函数(不止一个)、损失函数(可选)和待优化的参数块。

3.2 自动求导与解析求导

假设我们有一个残差，我们需要对残差求雅可比，如果将雅可比直接输到代码里，叫做解析求导，就是说已经解析式的，将求导的公式告诉算法了。自动求导是告诉代码残差和待求参数之间是什么关系，那么代码就可以自动的将雅可比求出来，不需要自己计算雅可比。

3.2.1 自动求导

以一个简单的例子来说明该问题，假设代价函数为：$f(x)=10-x$
则首先编写 CostFunctor 的代码如下：

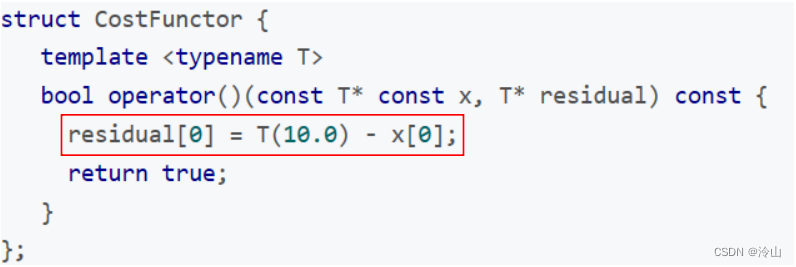
随后可直接构建 ceres 优化问题：

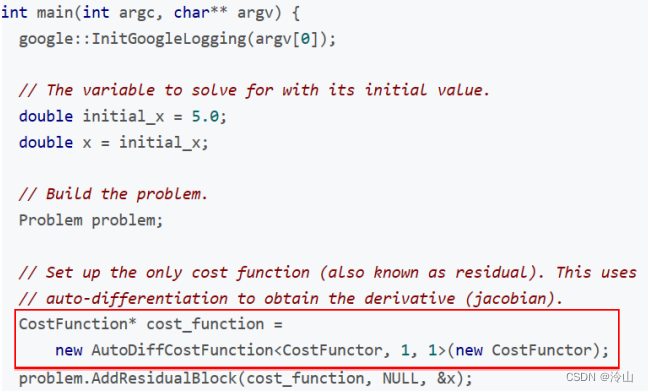
代码可以自动将导数求出来，可以看到代码残差函数相对于 $x$ 的导数等于 $-1$，但是没有任何一个地方告诉它有一个 $-1$ 的导数。

3.2.2 解析求导

解析求导的含义就是直接给出导数的解析形式，而不是ceres去推导。

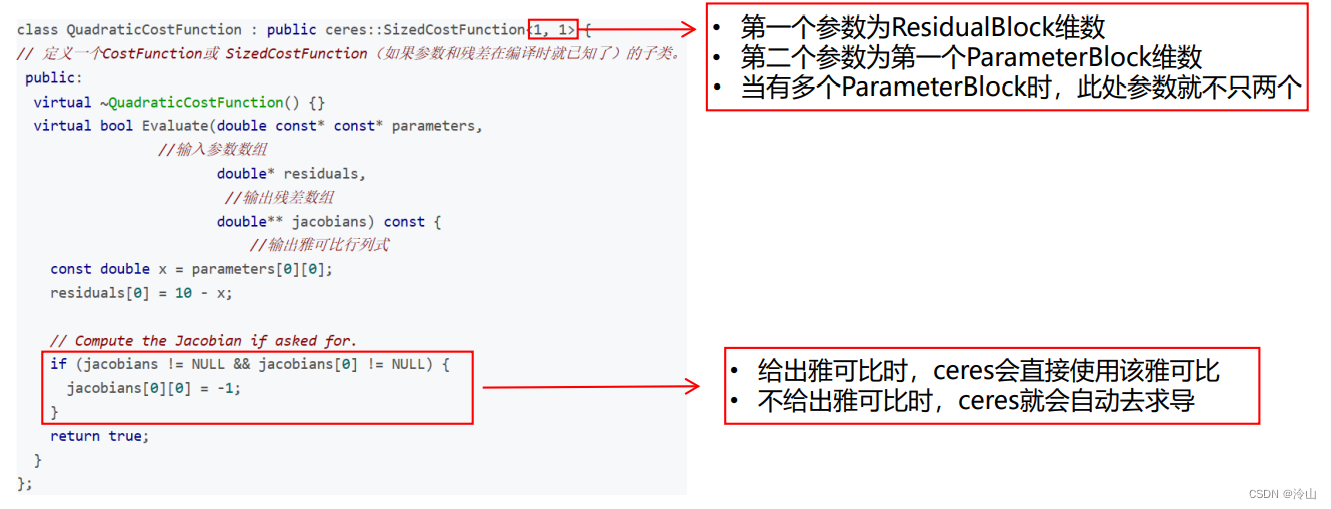
解析求导在没给出雅可比时，会转到自动求导上面去。

随后可构建优化问题：

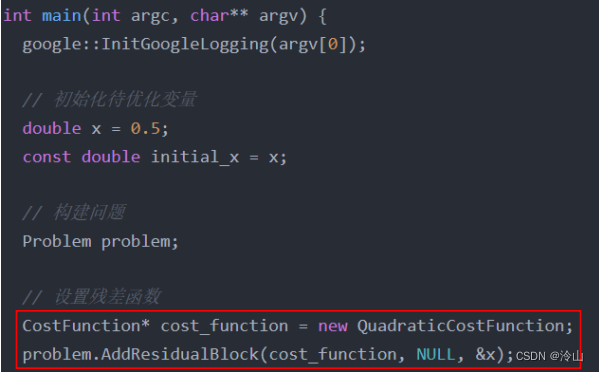
这种使用方式，就是vio/lio中使用ceres构建优化问题的方式。

3.2.3 自动求导与解析求导的对比

• 自动求导实现方便，但效率会比解析求导低 (比较 A-LOAM 和 F-LOAM )；
• 实际使用中，能够自动求导且效率没有形成障碍的，优先使用自动求导；
• 除这两种方法外，还有数值求导（SLAM问题中不常见，不过多介绍）

3.3 自动求导实现位姿优化(A-LOAM)

3.3.1 线特征

使用第 2.1.1 节公式。

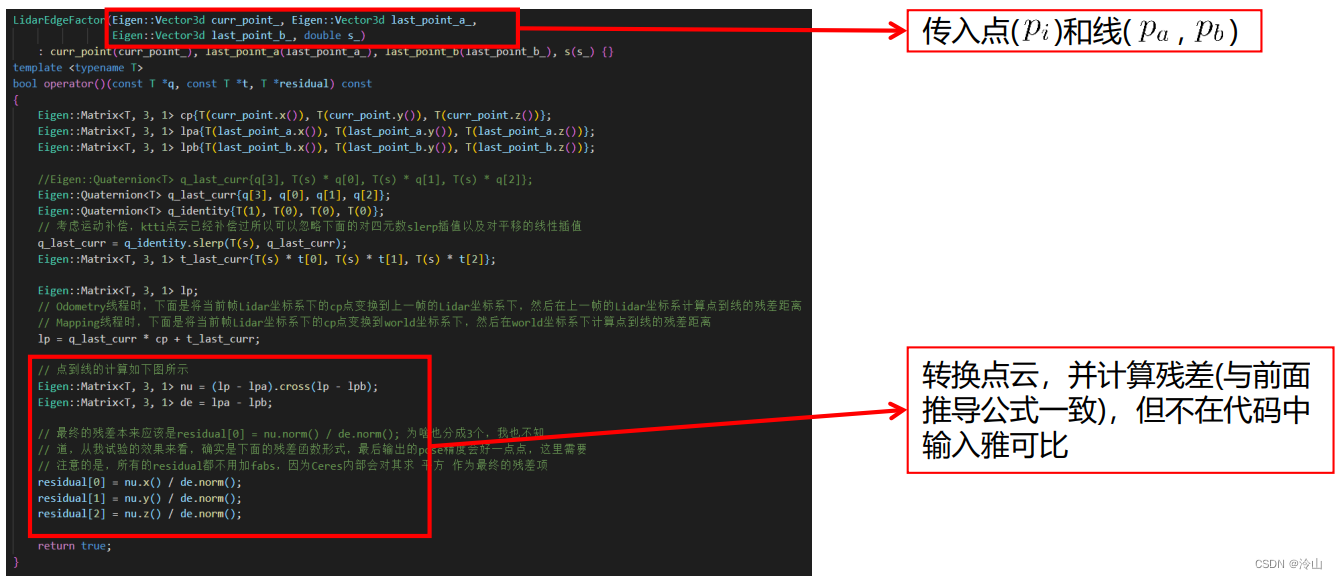
3.3.2 面特征

使用第 2.1.2 节公式。

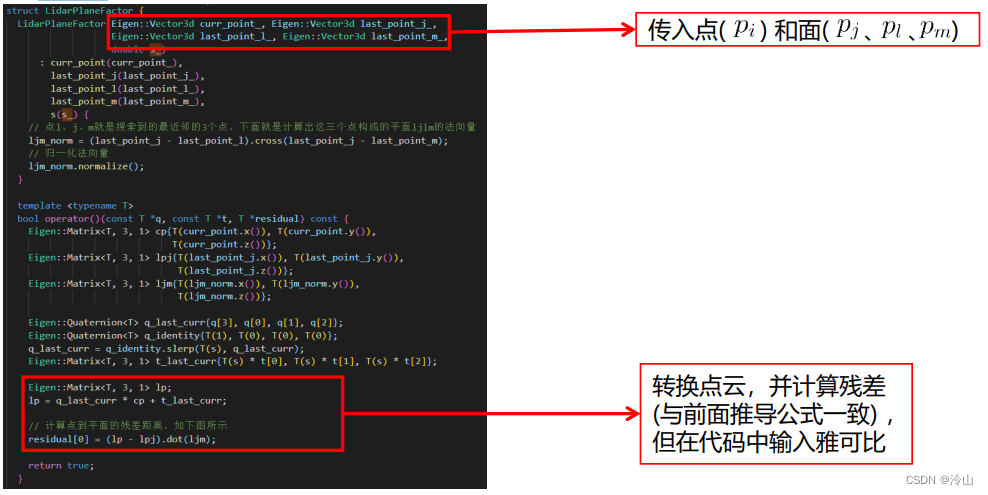
3.4 解析求导实现位姿优化(F-LOAM)

3.4.1 线特征

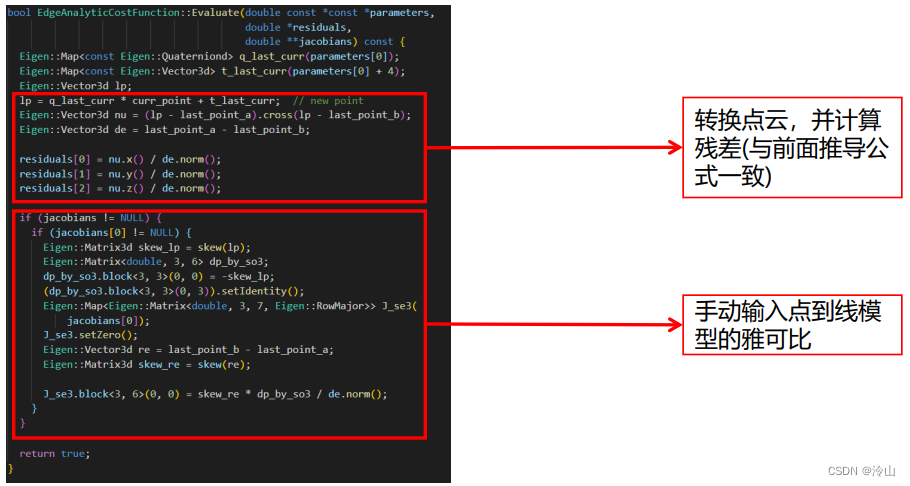
3.4.2 面特征

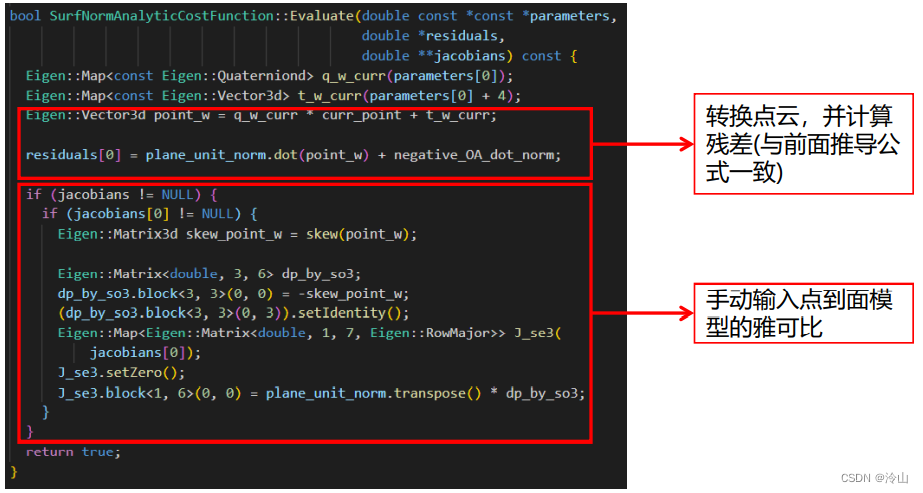
4. 相关开源里程计

4.1. 基于特征的里程计实现流程

帧到帧的方式，点云是比较稀疏的，会带来很多精度上的问题，比如：

1. 上一帧打到树上了，这一帧没了；
2. 上一帧和这一帧打到树上不同位置。

这时就引出了map的概念，也就是说，第$k+1$帧不是跟第$k$帧，而是第$k$帧之前的某些帧，共同构建出来了一个特征集合的map。不可能每一次都到map，map的运算量很大，那么实时性就没有意义了。这时就需要每隔几帧再跟map匹配。这样累计误差也不会特别大，效率精度都能保证。

4.2 LOAM

LOAM: Lidar Odometry and Mapping in Real-time, Ji Zhang and Sanjiv Singh
代码比较乱，很多是没必要的操作。

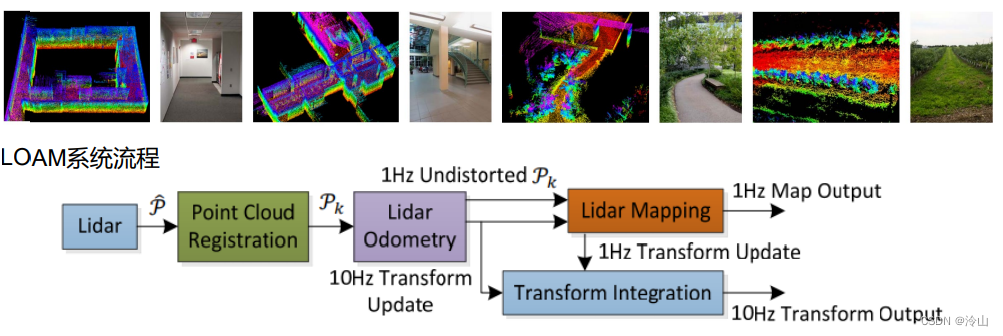
4.3 A-LOAM

主要特点

1. 去掉了和IMU相关的部分
2. 使用Eigen（四元数）做位姿转换，简化了代码（将sin、cos去掉了）
3. 使用ceres做迭代优化，简化了代码，但降低了效率(使用的自动求导)

4.4 F-LOAM(Fast LOAM)

主要特点

1. 整体和ALOAM类似，只是使用残差函数的雅可比使用的是解析式求导