概率论基础1

概率空间

概率空间由三部分组成

• sample space Ω
  就是我们对不确定的时间做实验，实验的所有结果(样本空间不包含重复的实验结果)，比如抛硬币，结果只会有正反面，所有样本空间为 Ω = { H , T } = { H e a d , t a i l } Ω = \{H,T\} = \{Head, tail\} Ω={ H,T}={ Head,tail}
• σ-algebra(F)
  先说event
  event是sample space的子集(按照某种标准分化的)，power set(σ-algebra)代表我们sample space结果中所有的可能(包含样本空间本身和空集)，比如样本空间是
  Ω = { H , T } = { H e a d , t a i l } Ω = \{H,T\} = \{Head, tail\} Ω={ H,T}={ Head,tail}
  那么我们的power event是
  F = { H o r T ， H ， T ， n u l l } F = \{H or T，H，T，null\} F={ HorT，H，T，null}
  我们还可以得出样本空间的子集S1,S2属于F则S1∪S2属于F，并且Ω也属于F，F有多少个元素呢？一共有2^Ω个Ω指的是Ω元素个数
• probability measure P
  P代表我们的一个函数，或者方法，这个函数或者方法用来量化我们所遭遇到的event的概率

例子我们的医生想对他所有的病人的胆固醇量做样本统计，假设样本空间为所有病人胆固醇的值，按照一个标准将样本空间划分成三个event，分别是L(low cholesterol), B(borderline-hight), H(high cholesterol),那么他们的σ-algebra(power event)就是如下
F : = { L ∪ B ∪ H , L ∪ B , L ∪ H , B ∪ H , L , B , H , ∅ } F := \{L ∪ B ∪ H, L ∪ B, L ∪ H, B ∪ H, L, B, H, ∅\} F:={ L∪B∪H,L∪B,L∪H,B∪H,L,B,H,∅}

对于P的计算非常简单，无非就是用event的数量除以sample space，并且有以下的式子,A和B都是一个事件，都是样本空间Ω的子集，他们的并集的P是
$$P(A\cup B)=\frac{outcomeinAorB}{total}=\frac{outcomeinA+outcomeinB}{total}=P(A)+P(B)$$
那么我们的样本空间Ω的p是多少？
$$P(\Omega )=\frac{outcomesin\Omega }{total}=\frac{total}{total}=1$$

定义1:在σ-algebra(power set)之上我们可以定义P(probability measure)函数

比如我们event属于(∈)σ-algebra(power set)，且P(S)>=0
我们还可以得出假设样本空间的序列$$S_1,S_2,....,S_n\in F$$且所有F的子序列不相交(F就是power set也是σ-algebra)，那么我们可以得出$$P({\cup }_{i=1}^n{S}_i)=\sum _{i=1}^{n}P(S_i)$$,我们还可以得出event 0的概率测度为0因为不可能发生
$$P(ø)=0$$
假设2个event，A和B且A包含B则(event就是样本空间的子集)
$$P(A)<=P(B)$$
无论event A和event B相不相交都可以得出
$$P(A\cup B)=P(A)+P(B)-P(A\cap B)$$
上面的式子可能有一些疑惑，因为event A和event B如果相交，那么我们取A和B并集的probibility measure只是简单的相加就不对，因为他们相交，有的子集重合，所以要减去这个重合的子集所以会减去一个交集

条件概率

首先我们要区分dependent event和independent event(这个后面有讲)，我这里直接解释P(S’|S)，他的意思就是当event S已经发生，那么S‘的概率是啥，公式如下，具体解释看这里，P(S’∩S)代表S’和S同时发生的概率(这里是dependent event，起使independent event也是一样)

https://www.mathsisfun.com/data/probability-events-conditional.html
看完这个可能有疑问为什么要用第一次拿蓝球的概率乘第二次拿蓝球的概率？我们可以穷举法，将5个球标号，然后列出所有可能一共20个，最后2次都是蓝球的就2个最后概率为2/20,正好等于第一次拿蓝球的概率乘以第二次拿蓝球的概率

$$P(S^{\prime }|S)P(S)=P(S^{\prime }\cap S)->P(S^{\prime }|S)=\frac{P(S^{\prime }\cap S)}{P(S)}$$
为什么要取交集？因为我们2个条件是交互的要满足条件1的event，也要满足条件2的event,最后除以S的probibility measure是因为我们问题是问S的probability measure，且P(S)不能为0，也就是说我们的最终的问题不能是零概率，假设S’和S不相交，那么P(S’|S) = 0

通过上述同事我们还可以推
$$P(S^{\prime }|S)P(S)=P(S^{\prime }\cap S)orP(S|S^{\prime })P(S^{\prime })=P(S^{\prime }\cap S)$$

上面的式子还可以通过链式法则推广…如下
假设存在概率空间$$(\Omega ,F,P)$$并且,$$S_1,S_2,...$$是一系列event，且是F的子集那么
$$P({\cap }_i{S}_i)=P(S_1)P(S_2|S_1)P(S_3|S_1\cap S_2)...=\prod _{i}P(S_i|{\cap }_{j=1}^{i-1}{S}_j)$$
上面式子看起来有点奇怪怎么理解?假设i等于3，那么我们带入公式如下
$$P(S_1\cap S_2\cap S_3)=P(S_1)P(S_2|S_1)P(S_3|S_1\cap S_2)$$
我们把等号右边的前2项看成一个整体就简单多了

这里再提及一个概念叫做partition of Ω，指的是一些set比如A1,A2,A3,A4,A5…不相交并且样本空间Ω=A1∪A2∪A3…，那么A1,A2,A3,A4,A5…叫做partition of Ω,我们可以引申出下面的法则

law of total probability
假设有set A1，A2，A3…是partition of Ω(样本空间),且A1，A2，A3∈power set F，假设S∈F那么我们可以得出
$$P(S)=\sum _{i}P(S\cap A_i)$$
上面的式子没有什么难度，因为S也是F的一部分，A1，A2…也是F的一部分，S可能和某个A相交，也可能和大部分A不相交，那么对他们取交集累加就是S的概率，因为相交后交集为0那么概率还是0，根据上面式子我们再根据条件概率的公式得到
$$P(S)=\sum _{i}P(S\cap A_i)=\sum _{i}P(A_i)P(S|A_i)$$

例子，假设你的叔叔要去JFK飞机场，但是迟到并且下雨的概率P(late|rain)=0.75,迟到且不下雨的概率为P(late|no rain)=0.125,并且你查到明天要下雨的概率为P(rain)=0.2,那么他迟到的概率为多少?
因为要么下雨要么不下雨所以下雨和不下雨2个事件不相交且涵盖整个样本空间所以no rain , rain是partition of Ω,且rain的概率是0.2那么norain的概率岂不就是0.8？我们直接上law of total probability
$$P(late)=P(rain)P(late|rain)+P(norain)P(late|norain)=0.2\ast 0.75+0.8\ast 0.125=0.25$$
所以有1/4的可能迟到

贝叶斯(bayes定律)
我门要意识到一个问题，在条件概率下假设A和B都是样本空间的event，那么P(A|B)!=P(B|A)的
比如我们看NBA大部分的球员家里面可能有一个篮球(少部分没有)，那么我们样本空间就分为3类，有球，可能有，没有，那么我们将可能有叫做event probability_own_ball,没有求的event 叫做no_ball,那么这2个的条件概率天差地别，

• P(probability_own_ball | no_ball) 非常大因为它等于P(probability_own_ball ∩ no_ball) /P(no_ball)，因为NBA球员家里没有球的概率非常小，所以分母非常小，总体就非常大

• P(no_ball | probability_own_ball) 非常小因为它等于P(probability_own_ball ∩ no_ball) /P(probability_own_ball)，因为NBA球员家里有球的概率非常大，所以分母非常大，总体就非常小

那么我们想确定P(A|B)和P(B|A)的关系怎么办呢？这个时候就出现了我们的贝叶斯(bayes)定律
$$P(A|B)=\frac{P(A)P(B|A)}{P(B)}$$

我们可以推导
$$P(A|B)=\frac{P(A)P(B|A)}{P(B)}->P(A|B)P(B)=P(A)P(B|A)->P(A\cap B)=P(B\cap A)$$

independence

啥子是independence?就是2个event相互独立，互不影响，比如说抛色子，第一次抛和第二次抛互不影响，假设我们抛硬币3次，他的样本空间有8个(2^3),如下(H代表head，T代表Tail)
Ω={HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
假设我们有2个event，event A代表第三次是head朝上，event B代表第二次head朝上，所以
event A ={ HHH, HTH, THH, TTH }
event B ={ HHH, HHT, THH, THT }
so
P(A)=P(B)=4/8=1/2
P(A|B)=P(A∩B)/P(B)=1/2=P(A)
所以说假如A和B independence
$$P(A|B)=P(A)$$

再推广
A和B是independence
$$P(A|B)=P(A)->\frac{P(A\cap B)}{P(B)}=P(A)->P(A\cap B)=P(A)P(B)$$

啥子是dependent event，就是事件相互影响，当一个事件发生后会影响其余的事件概率，比如我们一个袋子中有5个球，3个蓝球，2个黄球，那么一个event叫做取出蓝球的概率是多少?且取出后不放回去，假如这个event发生后其余的event发生概率就要变，这就叫做dependent event

条件独立概率
有了条件概率，也一定会有条件独立概率，其定义如下
假设event A and event B都和event C( P( C)>0 )是condition independence那么
$$P(A|B\cap C)=P(A|C)$$
我们可以这样理解上面的式子，当event B和C是independent event他们的交集(同时发生B和C事件的概率)先发生了那么再发生A的概率是多少
$$P(A|B\cap C)=\frac{P(A\cap B\cap C)}{P(B\cap C)}=\frac{P(C)}{P(B\cap C)}\frac{P(A\cap B\cap C)}{P(C)}=\frac{1}{P(B|C)}P(A\cap B|C)=\frac{P(A\cap B|C)}{P(B|C)}$$
$$P()$$

例子：
假设我们有2个硬币，一个是正常硬币，一个是假的硬币(2面都是Head，也就是说这个假硬币P(H)=1),然后我们随机选一个硬币抛2次
样本空间Ω={H H, HT, T T}
event A:第一次抛的是H
event B:第二次抛的是H
event C:选到正常的硬币
我们注意A和B是不相关的，而和C是条件不相关的

不管你是independent event还是dependent event都可以用这个公式
$$P(A|B)=\frac{P(A\cap B)}{P(B)}$$

random variables

radom variables就是我们的一个未知数，它可以是我们随机实验中任何一个结果，比如我们抛硬币，只抛一次那么就只有2个结果，那就是H和T，假设H是1，T是0，那么random variables X可以是1也可以是0

random variables怎么和我们的样本空间联系起来呢？random variables可以是样本空间的任何一个数字，比如扔色子，样本空间就是Ω={1，2，3，4，5，6}，random variable可以是其中的任何一个，那么P(X=1)代表1的概率是多少

再举个例子，抛2次筛子，我们先构建样本空间Ω，因为样本空间不包含重复的实验结果，所以样本空间Ω为{2,3,4,5,6,7,8,9,10,11,12},我们的random variable可以写成5<=X <=8，如下
P(5 <= X <= 8)= P(X=5) + P(X=6) + P(X=7) + P(X=8)
我们还可以这样写P(X=x) = 1/12 问x是多少

random variable可以是离散的也可以是连续的
离散就是可数
连续就是不可数

离散random variable

这里说明一下样本空间所有的概率相加为1如下
$$\sum _{x\in \Omega }PX(x)=1$$

Bernoulli random variables
伯努利random variables就是样本空间只有2个的random variables，假设样本空间的一个样本为1，另一个为2，则
PX(0) = p -> PX(1) = 1 - p
indicator random variable
indicator random variable和伯努利相似，假设event A,当A发生的时候如下$$I_A=1$$当除了A event外的event 发生如下 $$I_A=0$$

geometric
假设我们抛硬币，抛硬币是Bernoulli random variables把，只有2个结果要么H要么T，假设我们H的概率是p，那么T的概率是(1-p)，且抛硬币是independent的，那么假设我们抛k次才抛到H那么抛k次是H的概率是
$$P(kflips)=P(1stflip=tail,...,k-1flip=tail,kthflip=head)=P(1stflip=tail)...P(k-1thflip=tail)P(kthflip=head)=(1-p{)}^{k-1}p$$

Binomial
首先考虑一个问题，我们抛硬币，抛n次，H的概率为p，问有k次是H的概率是多少？
假设我们前k次抛的都是H，后n-k次都是T，那么概率一共是
$$P(kH,n-kT)=p^k(1-p{)}^{n-k}$$
这个k可以为1也可以为n可变的
我们再说一个概念叫做Binomial，假设我们想知道一共抛三次硬币，有2个H的次数是多少，这里有个公式叫做Binomial，公式如下
$${(}_k^n)=\frac{n!}{k!(n-k)!}$$
此时我们考虑最后一个问题就是构造一个样本空间，我们假设抛n次硬币，有k次为H，按照这个条件构造样本空间，我们知道样本空间中每一个k个H的样本的概率是(一次H概率为p)
$$P(kH,n-kT)=p^k(1-p{)}^{n-k}$$
共$${(}_k^n)=\frac{n!}{k!(n-k)!}$$
样本，那么所有样本的概率一共为
$$\frac{n!}{k!(n-k)!}{p}^k(1-p{)}^{n-k}$$

poisson
泊松分布也是我们离散概率中常用的
先说泊松分布用在那里，用在我们计算事件在给定单元(时间，区域，体积)发生的次数，比如一天内car accidents，且

1. event发生是independently的
2. 假设在某一个时刻呼入的期望值为λ(不是总期望值，而是其中的一个为p(x)n=λ)

我们假设有一个呼叫中心，我们为了估计一天内有多少个客户呼入，以此来招聘员工，这个问题我们可以回到之前二项式分布时的方法(问题有点像，不过泊松分布将抛硬币问题连续抛3个硬币变成抛无限个硬币，因为时间可以划分为无限段)，我们假设将时间段化为n段，每一段呼入概率几率p，没有呼入概率记为(1-p),那么一天呼入k个电话，将时间段化为n段，那么一天呼入k个电话的概率为
$$\underset{n->\infty }{\lim }{(}_k^n)p^k(1-p{)}^k$$
最后等于
$$P(X=k)=\frac{{\lambda }^k}{k!}{e}^{-\lambda }$$

连续random variable

uniform distribution

首先我们不要忘记上面讲的random variable的X可以写成P(a<=X<=b)
然后我们介绍一下均匀分布(uniform distribution),指的是我们样本空间中所有的样本概率相等(画出直方图横轴为样本，纵轴为概率会看到为矩形)，假设我们样本空间从小到大排序为a到b那么我们的random variable 为a<=x<=b(a和b之间是不可数的因为他们是continued)，我们画个坐标轴最后发现这个均匀分布产出的矩形面积为1，假设这个均匀分布的横坐标为样本(continued)，纵轴为对应概率，那么概率为1/(b-a)

我们看到的是均匀分布，假设不是均匀分布而是正太分布呢(要知道大多数的样本是正态分布的)？我们要用微积分的知识求一个样本到另一个样本之间的概率(样本是continued)

比如时间就是一个连续的样本，假设一个时间段为样本，我们再假设每个样本的发生概率都一样，这样我们就可以组成一个均匀分布(横轴为时间，纵轴为发生概率)

PDF & CDF

probability density function(pdf)
我们用f(x)去model continuous random variable( f(x)为PDF ) ,比如说上面的图形，我们的fx就是上述的图形，且0<f(x)<1，因为概率不能为负

我们还要知道
$${\int }_{-\infty }^{+\infty }f(x)=1$$
因为所有的概率相加为1

假设我们有一个 random variableX满足$$f(x)=c{x}^3$$且样本是连续的，位于2和4之间，请问c为多少可以使这上述PDF为一个合法的概率分布?

首先我们谨记$${\int }_{-\infty }^{+\infty }f(x)=1$$，又因为概率分布再2和4之间，所以我们可以改成$${\int }_2^{4}c{x}^{3}dx=1$$$$c[\frac{x^4}{4}{]}_2^4=1$$$$60c=1$$$$c=\frac{1}{60}$$
第二问为样本3到4之间的概率是多少？就是积分的上下界改一下$${\int }_3^4\frac{1}{60}{x}^{3}dx$$那么我们的分布的中位数是多少？假设x=m为中位数那么$${\int }_{-\infty }^{m}f(x)dx={\int }_m^{+\infty }f(x)dx=\frac{1}{2}$$
还有个问题这个PDF的CDF(cumulative distribution function)是啥？

CDF是PDF的积分，PDF描述一个样本概率的变化，从第一个样本到最后一个样本概率都不一样，而CDF是描述这个概率变化的程度，比如我们的样本的概率是正态分布的，那么中间突出来两边低的一个图形，通过PDF的图形得知两边的概率低，中间的概率高，那么他的CDF是他的(PDF)的积分，从几何上来看，CDF的图形是从低到高，且$$\underset{x->-\infty }{\lim }CDF=0$$$$\underset{x->\infty }{\lim }CDF=1$$,因此CDF可以看为一个样本概率分布的情况，假设CDF开始比较陡峭说明样本前面的数字出现概率高，后面缓说明后面样本概率低

cumulative distribution function(CDF)的函数如下$${\int }_{-\infty }^{x}f(t)dt$$
其中f(t)为PDF
假设我们要计算样本x小于2.7的概率我们可以直接将2.7带入我们的CDF中

Exponential random variables(指数random variables AKA 指数分布)

其实各种分布都是在PDF上的差距，比如uniform distribution的PDF是一个矩形，说明每个样本的概率都一样，而指数分布顾名思义PDF是一个指数形状，样本x大于等于0，且样本越小概率P越高，样本x越趋于无穷大说明概率越来越小，指数分布的函数如下
f X ( x ) = { 0 , o t h e r w i s e λ e − λ x , i f x > = 0 f_X(x)=\{_{0, otherwise}^{λe^{-λx},ifx>=0} fX​(x)={ 0,otherwiseλe−λx,ifx>=0​

图形如下

gaussian分布 AKA Normal分布 AKA正态分布

正太分布是大多数样本的分布模型，其PDF如下
$$f(x)=\frac{1}{\sqrt{2\Pi }\sigma }{e}^{-\frac{1}{2{\sigma }^2}(x-\mu {)}^2}$$

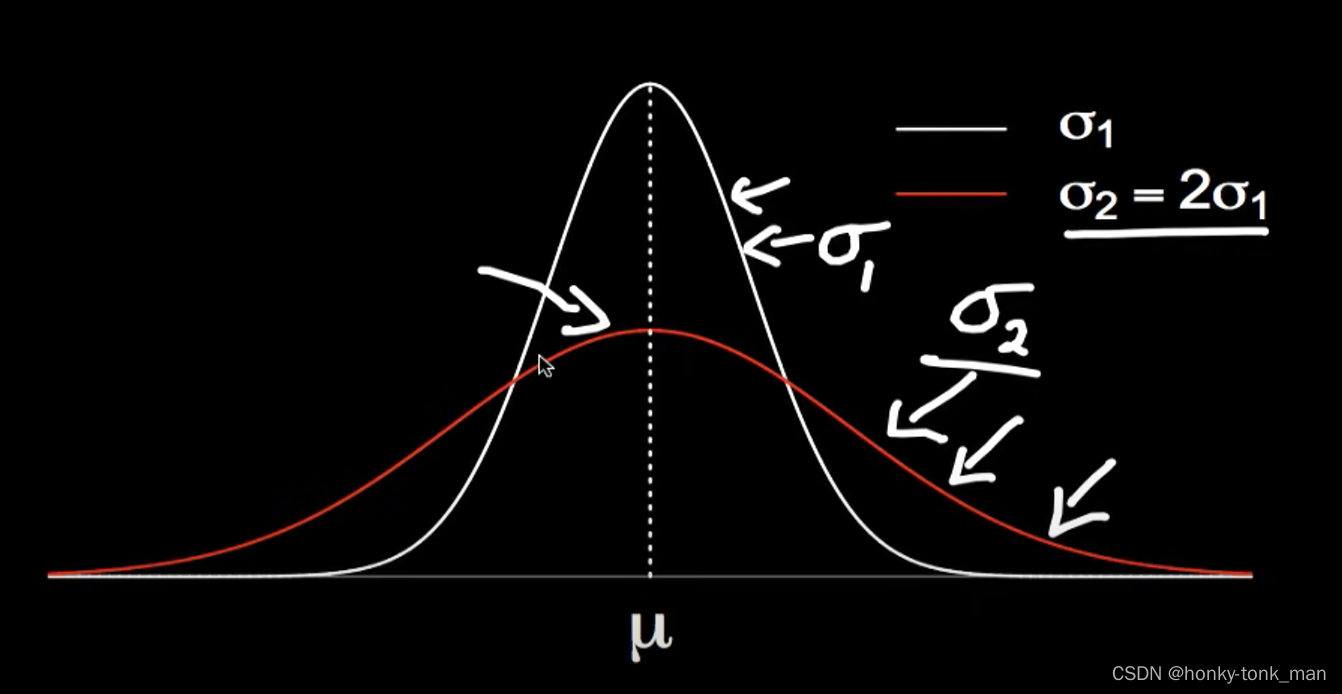
其中μ为这个分布的mean(且-∞<μ<∞)，σ是一个正值(一个标准偏差)

mean就是平均值，σ是标准差，σ的平方是方差，样本之间越分散那么标准差就越大

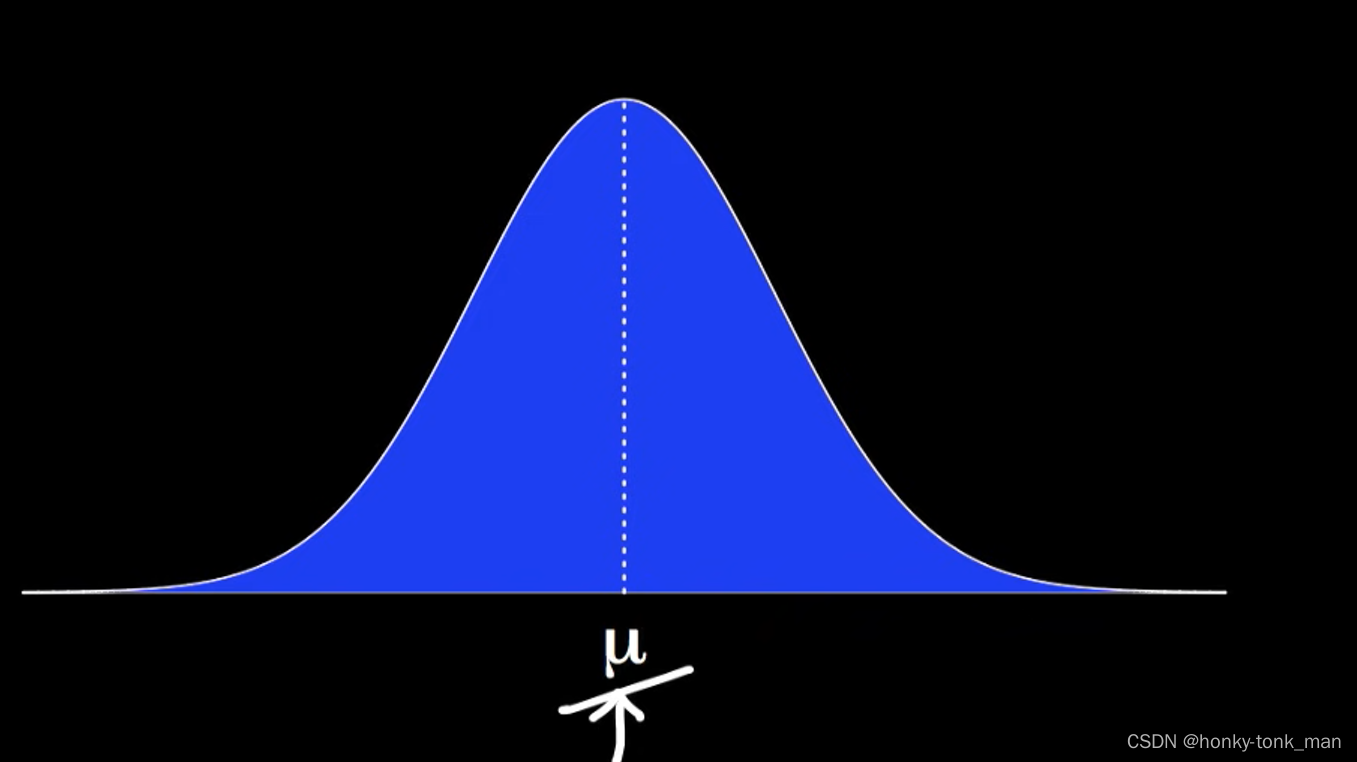
如上图所示μ就是期望值，
假设我们以μ为中心左减一个标准偏差σ，右加一个标准偏差σ，这样(μ-σ，μ+σ)那么这个区间内的概率为0.68如下图

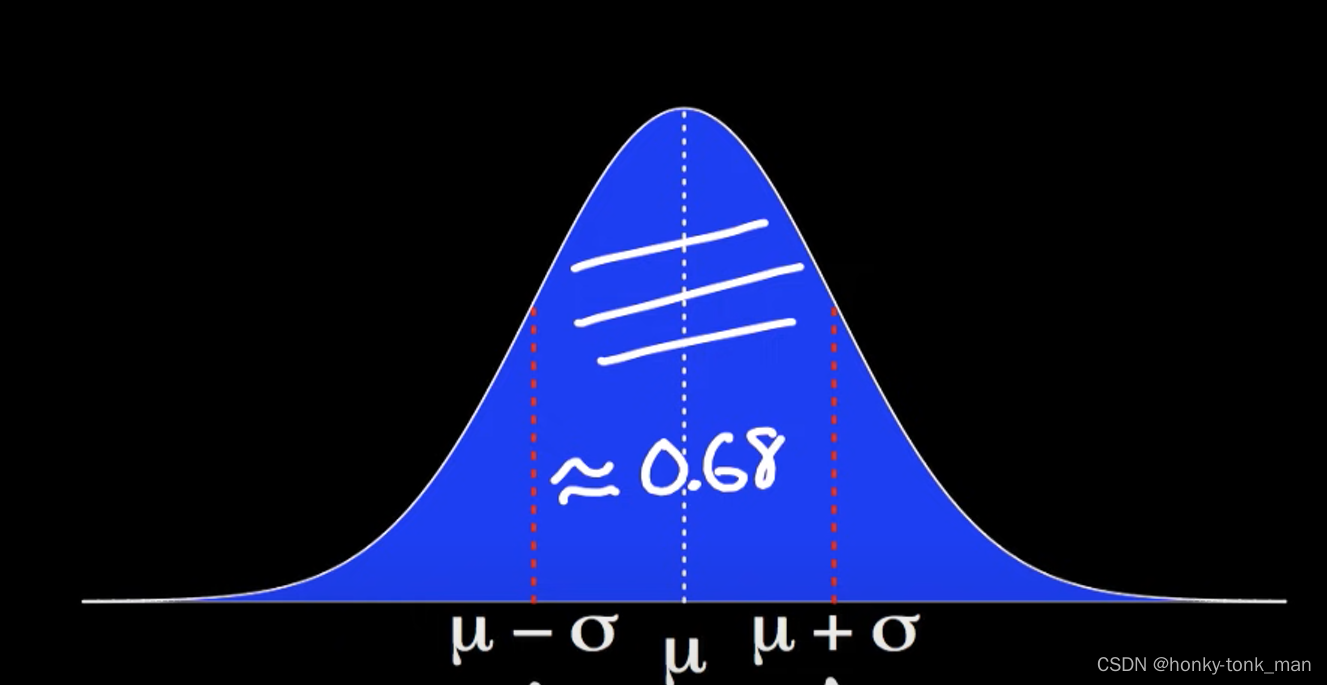
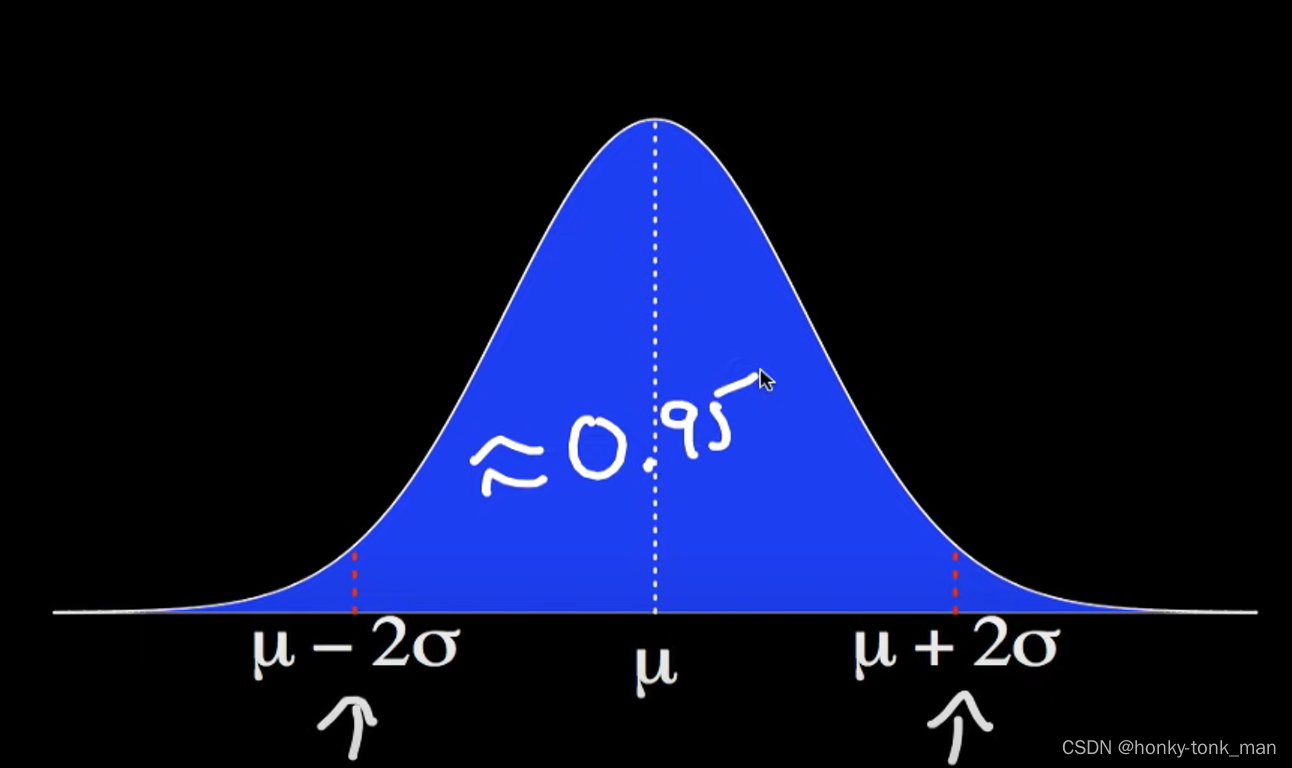
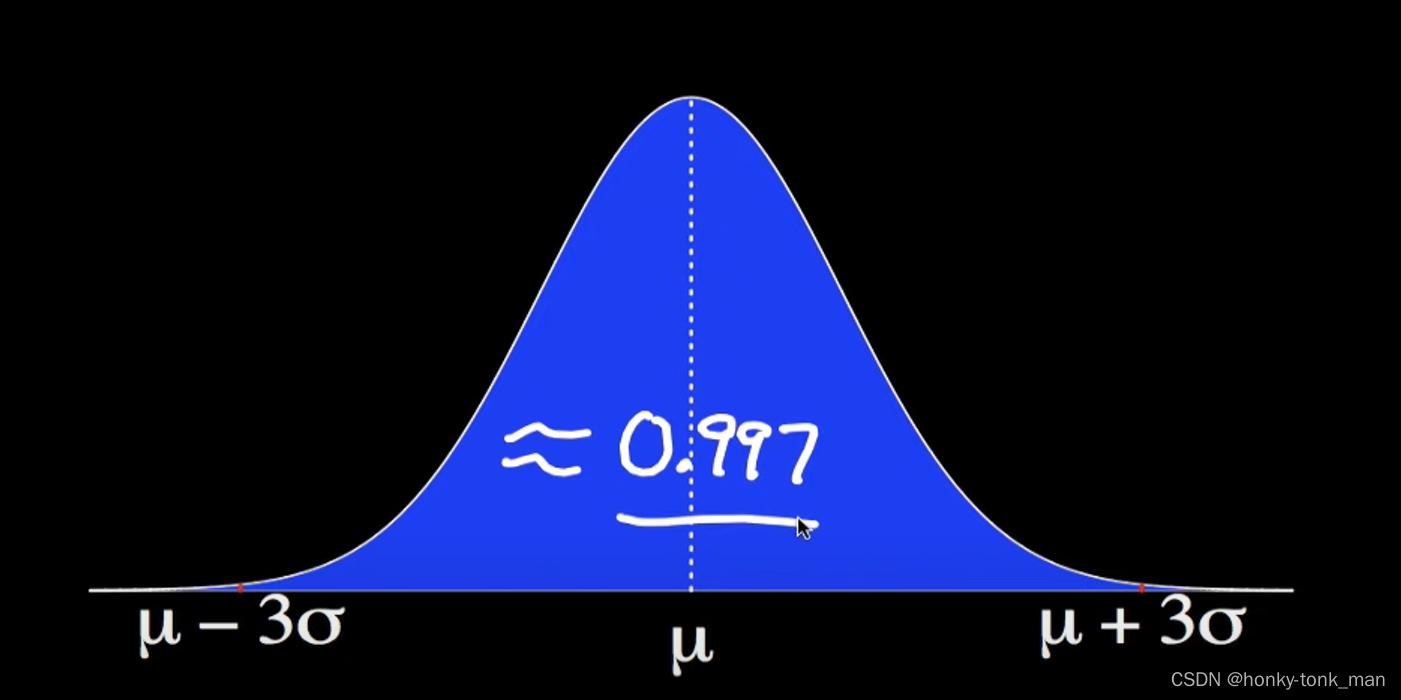
假设我们有一个正态分布，其期望值为μ，标准差为σ，X为标准分布随机变量，那么我们可以记为
$$X\tilde{}N(\mu ,{\sigma }^2)$$

标准正太分布随机变量
首先我们定义一个Z，其定义如下(x是我们一个样本的值)$$Z=\frac{x-\mu }{\sigma }$$，这就将一个正太分布化成一个标准正太分布，为什么要这么做?因为我们用原来的正太分布不太好估算值比如X大于特定值的概率(因为不同的正太分布有不同的标准差和期望值)，我们将其化成标准的正太分布就是将那么多不同的正太分布标准化，为了好求值，因为标准正态分布值都一样，可以轻而易举用软件算出对应的值

假设我们对人身高分布的数据做估算，其标准差为7.1，期望值为176.3，我们要求身高在170到180之间的比例，如果用正太分布不太好估算其值，我们就将其标准化化成一个统一标准的正太分布图
$$P(170.0<x<180.0)->标准化X化为Z->P(\frac{170-176.3}{7.1}<Z<\frac{180-176.3}{7.1})=P(-0.887<Z<0.521)$$

此时我们已经得到标准正太分布的范围，然后用matlab等工具可以直接求值得到
$$P(-0.887<Z<0.521)=0.511$$

Functions of Random Variables

PS:说实在我不知道他实际上的意义是啥
首先为什么叫做Functions of Random Variables?我们的Random Variables是X，那么前面加上一个function顾名思义是将X当成方程里面的x整成一个式子，比如y=2|x|，然后我们求y的概率，也就是通过一个式子将样本空间中的X映射成另一个样本空间中的Y，

比如我们有一个样本空间s1{-1,0,1,2,3},此时我们有一个random variable X 且PX(s1)=1/5，此时我们通过一个式子Y=2|X|,将s1转换成s2，则s2为{0,2,4,6},此时s2的random variable为Y(Y=2|X|)然后我们求s2的PMF，我们直接先列出s2的PMF如下
$$PY(0)=P(Y=0)=P(2|X|=0)=P(X=0)=1/5$$
$$PY(2)=P(Y=2)=P(2|X|=2)=P(X=-1)orP(X=1)=2/5$$
以此类推

Conditional probability mass function

顾名思义就是conditional probability加上PMF
其中conditional probability讲的是2个event其中一个为另一个的condition，求其中一个event的概率，而PMF讲的是样本空间中每个样本的概率，我们要将其结合起来，比如event C已知的时候PMF怎么变化$$P_X(x_i|C)=P(X=x_i|C)=P(A_i|C)=\frac{P(A_i\cap C)}{P(C)}$$

假设我们抛硬币5次，在我已经看到2个硬币的情况下我想知道n个Head的概率

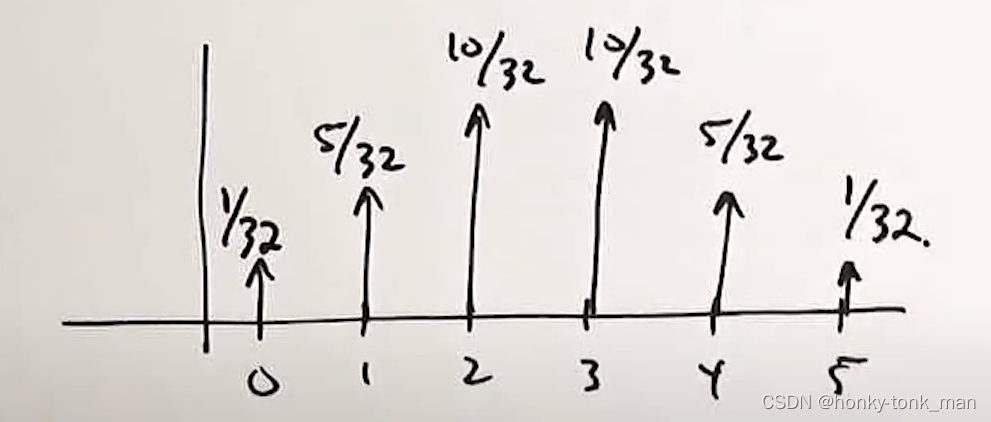
这个问题我们已经看到2个硬币这个是event，也是condition，然后我们想知道n个Head的概率，此时我们可以先画一个二项式分布的图，横坐标代表几个head，纵坐标代表概率P

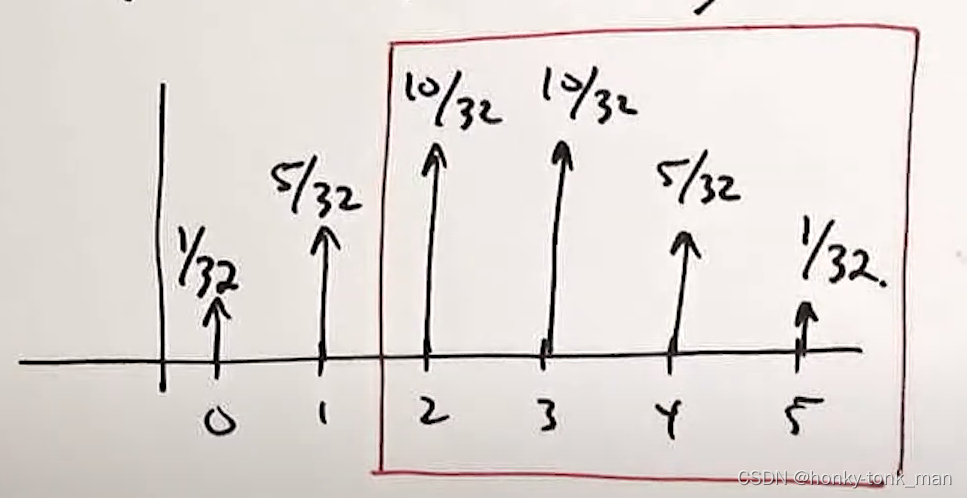
此时因为X要大于等于2，因为我们的条件event C就是说我们已经看到有2个头，所以在上图的坐标轴的x轴的1和2之间画一个线

此时我们知道了当X大于2(至少2个头在上面)的情况的概率为$$P(X>=2)=\frac{10}{32}+\frac{10}{32}+\frac{5}{32}+\frac{1}{32}=\frac{26}{32}$$
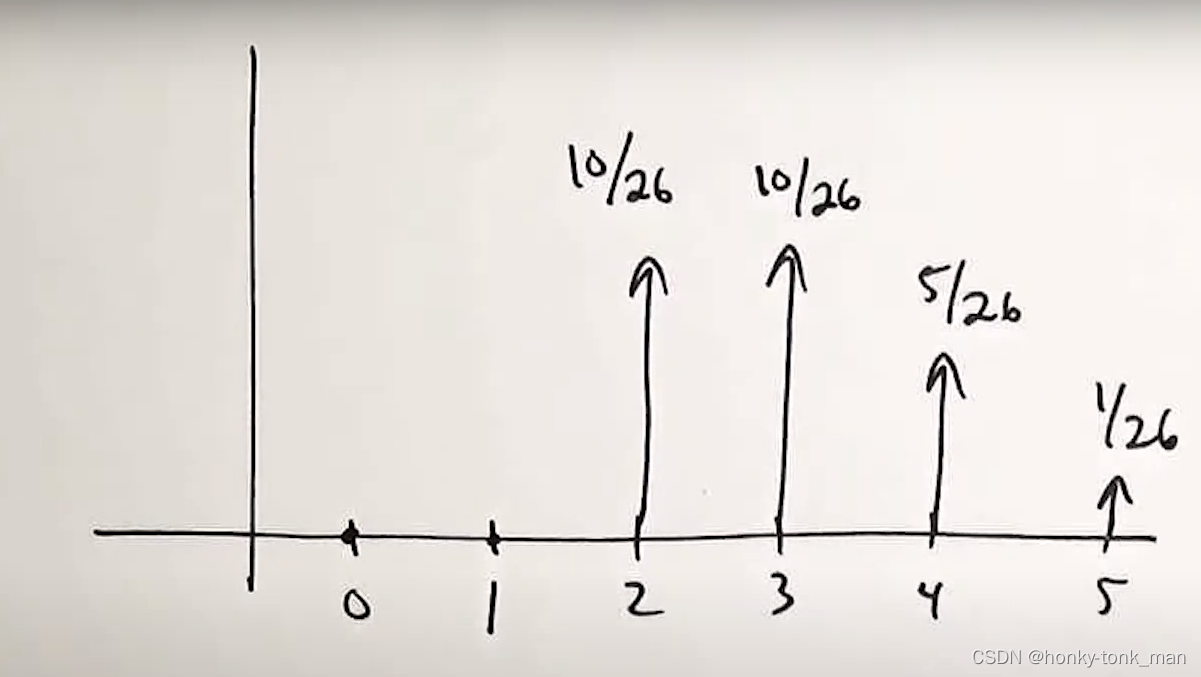
然后我就知道了P(X=2|X>=2)=(10/32)/(26/32)到P(X=5|X>=2)=(1/32)/(26/32)的概率，新的PMF图如下,因为0和1不会发生，因为不在条件event C的范围内

综上述的例子，我们可以得出以下的结论

• PX(Xi|C) >0
• $$\sum _{xi}PX(xi|C)=1$$

mean VS avg VS expected value

很多时候这三个概念容易搞混，这里记录一下，因为在random variable下Expected value等于mean，而mean的计算方式又和avg有点像，所以这里特别记录一下

首先avg也叫做arithmetic mean，mean也分geometric mean和arithmetic mean(avg)，知道了arithmetic mean也是avg，那么geometric mean是啥呢？顾名思义就是几何平均值，他的计算公式是假如我们有n个样本{X1,X2…Xn}，那么他们的几何平均值为$\sqrt[n]{X1\ast X2\ast ...\ast Xn}$,假设我们画一个2D的长方形，几何平均值就是将其变成一个正方形，次正方形的面积和变换之前的长方形面积一样，且geometric mean主要用于不同属性样本之间的平均值
这个时候我们考虑以下我们的expected value和mean(arithmetic mean)的区别,假设样本的概率都是一样的，那么expected value等于mean，假如概率不一样就不等于，这个没有什么争议，但是在random variable下expected value一定等于mean，比如下面的例子

因为random variable一定可以展开，比如我们的random variable如下

num	prob
1	$\frac{1}{5}$
2	$\frac{2}{5}$
3	$\frac{3}{5}$

mean(avg)：$\frac{1}{5}+\frac{2}{5}+\frac{2}{5}=\frac{11}{5}=2.2$
关于random variable这里要展开得到样本为{1,2,2,3,3}，$E=1\ast \frac{1}{5}+2\ast \frac{1}{5}+2\ast \frac{1}{5}+3\ast \frac{1}{5}+3\ast \frac{1}{5}=\frac{11}{5}$
所以在random variable下他们是相等的

我们对比一下2者的区别

avg	mean
An Average can be defined as the sum of all numbers divided by the total number of values.	A mean can be defined as an average of the set of values in a sample of data.