积分图像文章推荐:http://blog.sina.com.cn/s/blog_4cb0b54301017wwo.html
https://blog.csdn.net/u010807846/article/details/50354000
参考文献:
[1] Viola P., Jones M. J. Rapid Object Detection Using a Boosted Cascade of Simple Features. Computer Vision and Pattern Recognition, 2001, Volume 1, 8-14.
[2] Lampert C., Blaschko M., Hofmann T. Efficient subwindow search: A branch and bound framework for object localization. IEEE PAMI 31(2009)2129-2142.
[3] F.Porkili. Integral Histogram: A fast way to extract histograms in cartesian spaces. In Proc.IEEE Conf. on Computer Vision and Pattern Recognition(CVPR), 2005.
在[1]中,有两个重要的思想:
1 级联弱分类器可以组成强分类器,且最终的结果可以媲美甚至于超越很多强的分类器。这也是至今仍然常用的一种分类器框架---Ensemble Classifier。
2 为了能够快速实时有效的检测物体,利用pre-compute理念,形成积分图像的模式。到要用到pixel值的时候,一个矩形框的像素可以通过4次简单的查表得到,在Real-time下非常的实用。也是至今仍然很多人借用的方法之一。
积分图像:
先看这个最原始的玩意。给定一副图像(最好是灰度scale,彩色的话需要对每一个通道都要计算)。灰度值如下图所示:

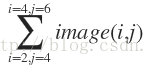
公式1:i,j代表位置,image代表图像
很显然,如果只是针对小区域的话,这样的加减倒也不是很复杂,如果这个区域包含成千上万的像素,那计算起来就比较复杂了。所以随着计算区域的增大,时间复杂度增长也很快。
那有没有一种比较简单的方法,可以无论需要计算的区域有多大,它的时间复杂度都不变呢,或者变化很小。这就是积分图像最初的考虑策略,尽量减少后续的计算以达到实时的效果。
积分图像,顾名思义,对每一个点的像素值,做相应的积分,其实简单表达就是每一个点的像素值就等于在这之前所有像素值的和。将图1转化为积分图像如图2:

图2:图1的积分图像
现在计算图中深度区域的值就可以很简单利用4次差别结果得到:120 - 42 - 21 + 6 = 63。
怎样利用积分图像来计算任意矩形框的值呢?一般来说简单作4次查表,再简单的“--+”运算即可得到矩形框里面的灰度和。
解释:
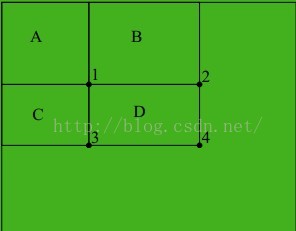
图3:积分图像计算
区域1 : = sum(A);
区域2 : = sum(A + B);
区域3 : = sum(A + C);
区域4 : = sum(A + B + C + D);
所以,如果需要计算D区域中的灰度和,则
sum(D) = 区域4 - 区域2 - 区域3 + 区域1 (都是灰度值)。
很明显,这里仅仅只需要通过查表得到 1、2、3、4点的积分图像的值即可得到。
这其实就是积分图像最妙的地方,通过简单的预计算处理,存储整幅图像的积分图像,通过4次快速查表,便可以得到一个矩形框中的灰度和。下图是计算积分图像的公式:
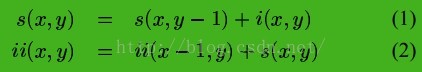
公式2
直接利用[1]中的解释:s(x,y)是row的积分值,ii(x,y)就是最终的积分图像。
正因为积分图像实现简单,速度快,从提出以后,后面相应的出现了更多在此基础上做文章的研究。例如“Sub-Window Search”[2]也是通过利用积分图像的原理,从全局进行深度搜索,最终得到一个比较好的定位。另外,[3]也是在原始的灰度积分图像上做出的一点扩展,将这种快速算法扩展到直方图的计算上来,也可以很好的进行图像的定位。
积分直方图:
还是利用图1中的灰度作为例子。在积分直方图中,最小的积分单元不再是灰度,而是灰度或者彩色的直方图。如果对于图1中,选择9个bin作为基,则将图1通过转化每个bin的
频率,如图4所示:
图4:频率图
参考直方图的概念[4],不作详细解释为什么会是这样的频率。
但是,想把上面的图变成积分图的形式,与最初的积分图像不一样的地方在于,并不能把这些数字积分相加起来,而应该把
每一部分的bin进行对应的处理。即bin与bin之间的相加。例如在图中点(1,1)处的bin与点(1,2)处的bin如下图:
图5:左图为点(1,1)处原始直方图,右图为点(1,2)处
的原始直方图
而点(1,2)处的积分直方图为点(1,1)处的原始直方图加上点(1,2)处的原始直方图(对应的bin)相加。得到结果如下图:
图6:积分直方图
在点(1,2)处利用积分的思想,存入的值应该是上图的直方图。以此类推,后面的每一个点的直方图都是前面所有点的直方图的和。
其实积分直方图的过程包括计算积分以及后续的查表得到某一个区域的值都与积分图像非常的相似。
心得:
积分图像的好处就在于能够很快的处理某一个区域的值,但如果预计算包括预存储的空间非常的大,也可能这种空间换时间的方法就不再成为通用的解决办法。