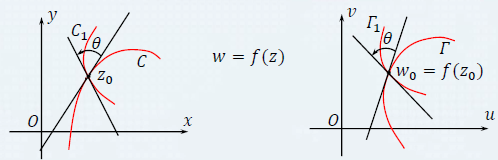复变函数和积分变换(Complex Function & Integral Transform I)
复变函数和积分变换(Complex Function & Integral Transform II)
复变函数和积分变换(Complex Function & Integral Transform III)
参考文献:
mooc国防科技大学《复变函数》
王忠仁、张静《工程数学:复变函数和积分变换》
焦红伟、尹景本《复变函数与积分变换》
梁昆淼《数学物理方法》
级数(Series)
复变函数项级数(Complex Function Series)
-
复数项级数(complex number series):设
{zn}=z1,z2,⋯,zn,⋯ 为一复数序列。
(1) 称表达式
n=1∑∞zn=z1+z2+⋯+zn+⋯ 为复数项无穷级数。
(2) 称
Sn=z1+z2+⋯+zn为级数的部分和
(3) 若极限
n→∞limSn=S 存在( S 为有限数),则称级数是收敛的, S 称为级数的和;如果序列
{Sn}不收敛,则称级数是发散的。
复数项级数收敛的充要条件:设
zn=xn+iyn(n∈Z+) ,则
n=1∑∞zn收敛
⟺n=1∑∞xn,n=1∑∞yn都收敛
复数项级数收敛的必要条件:
n→∞limzn=0⟹n=1∑∞zn 收敛
定理 1:如果
n=1∑∞∣zn∣ 收敛,则
n=1∑∞zn 收敛,并且
∣n=1∑∞zn∣⩽n=1∑∞∣zn∣
(1) 如果
n=1∑∞∣zn∣ 收敛,则称级数
n=1∑∞zn绝对收敛(absolutely convergent)。
(2) 非绝对收敛的收敛级数称为条件收敛(conditionally convergent)。
由于
n=1∑∞∣zn∣是正项级数,其收敛性可以用正项级数的相关定理来进行判别。另外,还可得到
n=1∑∞∣zn∣收敛的充要条件是
n=1∑∞xn,n=1∑∞yn都绝对收敛
-
复变函数项级数:设区域D上的函数列
{fn(z)}=f1(z),f2(z),⋯,fn(z),⋯
(1) 称
n=1∑∞fn(z)=f1(z)+f2(z)+⋯+fn(z)+⋯为区域D 内的复变函数项级数(series)。
(2) 该级数的前n 项和
Sn(z) 称为这个级数的部分和((partial sum))。
(3) 如果对于区域D 内的某一点
z0 ,极限
n→∞limSn(z0)=S(z0)存在,则称级数
n=1∑∞fn(z)在
z0点收敛(convergence),称
S(z0)为它的和(sum)。
(4) 如果级数在 D 内处处收敛,那么它的和一定是与z有关的一个函数
S(z)=f1(z)+f2(z)+⋯+fn(z)+⋯,这个函数称为级数的和函数(summable function)。
关于复数项级数与复变函数项级数,由于这两类级数的有关定义、性质与判别法与高等数学的相应部分极为相似,所以,不再赘述。
(5) 一致收敛(uniform convergence):如果对于任意
ϵ>0 ,存在
N>0,对于任何的
z∈D,当
n>N时,恒有
∣k=1∑nfk(z)−f(z)∣<ϵ,∀x∈D,则称级数
n=1∑∞fn(z)在D上一致收敛于函数
f(z)
定理 (Weierstrass M-test):如果级数
n=1∑∞fn(z)在区域
D满足条件:
(i)
∀z∈D,∣fn(z)∣⩽Mn(n=1,2,⋯)
(ii)正项级数
n=1∑∞Mn收敛
则级数
n=1∑∞fn(z)在区间
D上一致收敛
(6) 内闭一致收敛(Closed uniform convergence):设函数
fn(z)(n∈Z+) 定义在区域G 内,若级数
n=1∑∞fn(z)在G 内任意一个有界闭集上均一致收敛,则称该级数在区域G 内内闭一致收敛于
f(z)。
定理:如果级数
n=1∑∞fn(z)在区域
D内解析,级数
n=1∑∞fn(z)在D内内闭一致收敛于
f(z),则
(i)
f(z)在D内解析
(ii)
f(p)(z)=n=1∑∞fn(p)(z)(p∈Z+)
幂级数(Power Series)
-
幂级数(Power Series):称形如
n=0∑∞an(z−z0)n=a0+a1(z−z0)+⋯+an(z−z0)n+⋯的级数称为幂级数,其中
z0,a0,a1,⋯,an,⋯为复常数。
特别令
z0=0 有
n=0∑∞anzn,只要做变换
ξ=z−z0即可化为一般形式,为了方便常讨论此形式。
-
幂级数的收敛圆(circle of convergence)
阿贝尔(Abel)定理:若级数
n=0∑∞anzn在点
a(a=0) 收敛,则它在圆域
K:∣z∣<∣a∣ 内绝对收敛;在闭圆
K1:∣z∣⩽ρ(ρ<a)上一致收敛。
若级数
n=0∑∞anzn在点
b(b=0) 发散,则它在
∣z∣>∣b∣ 时发散。
有了阿贝尔定理便可弄清幂级数的收敛范围。
首先,幂级数在点z =0 是收敛的。
其次,幂级数在z ≠0 时只有三种可能:
(1) 幂级数在复平面所有的点收敛(如
1+1!z+2!z2+⋯+n!zn+⋯);
(2) 幂级数在复平面所有的点发散(如
1+2z+22z2+⋯+2nzn+⋯);
(3) 存在一个圆域
∣z∣<R,幂级数在圆域内收敛(且绝对收敛),在
∣z∣>R上幂级数发散。圆周
C:∣z∣=R称为该级数的收敛圆(circle of convergence),R称为该级数的收敛半径(radius of convergence)。
为了统一起见,对于幂级数在复平面收敛,规定
R=+∞,对于幂级数仅在一点 z =0 收敛,规定
R=0。
定理 1:设幂级数为
n=0∑∞anzn,幂级数收敛半径的具体求法,同实函数一样,比值法和根值法是最常用的有效方法。
(1) 比值法:若
n→∞lim∣anan+1∣=λ 则收敛半径为
R=λ1
(2) 根值法:
n→∞limn∣an∣
=ρ 则收敛半径为
R=ρ1
实例:
- 求幂级数
n=0∑∞zn的收敛半径
解:级数的部分和
Sn=1−z1−zn(z=1)
(1) 当
∣z∣<1时,有
n→∞limzn=0,从而
n→∞limSn=1−z1,级数收敛
(2) 当
∣z∣⩽1时,级数的一般项
zn不趋近于零,级数发散。
由阿贝尔定理知级数的收敛半径为
R=1,并且函数
1−z1=n=0∑∞zn(∣z∣<1)
- 函数
z−b1也可通过变换表示成幂级数
z−b1=(z−a)−(b−a)1=−b−a1⋅1−b−az−a1
当
∣b−az−a∣<1时,即
∣z−a∣<∣b−a∣,可以得到
z−b1=−n=0∑∞(b−a)n+11(z−a)n
- 和函数的解析性
定理 2:设幂级数
n=0∑∞an(z−z0)n的收敛半径为R,则
(1) 它的和函数
f(z) 在收敛圆内解析
(2) 幂级数在收敛圆内可逐项求导任意次,即
f(k)(z)=n=0∑∞[an(z−z0)n](k)
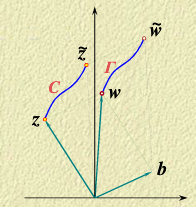
(3) 幂级数在收敛圆内任一曲线C 上逐项积分,即
∫Cf(z)dz=∫z0zf(z)dz=n=0∑∞n+1an(z−z0)n+1
泰勒级数(Taylor Series)
-
泰勒定理:若函数
f(z)在区域D内解析,圆域
K:∣z−z0∣<R含于D,则在K内有
f(z)=n=0∑∞an(z−z0)n,其中
an=n!1f(n)(z0)(n=0,1,2,⋯)
且上述展开式是唯一的,上式被称为泰勒展开式(Taylor expansion),它右端的级数称为泰勒级数。
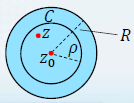
证明: 取一点
z∈K,做圆周
C:∣z−z0∣=ρ 包含点 z
由柯西积分公式有
f(z)=2πi1∮Cξ−zf(ξ)dξ
由于
∣ξ−z0z−z0∣<1,有上节实例可知
ξ−z1=n=0∑∞(z−z0)n+1(ξ−z0)n ,带入上式可得
f(z)=n=0∑∞an(z−z0)n,其中
an=n!1f(n)(z0)
关于展开式的唯一性,证明略。
推论:将泰勒定理和上节的定理2结合,可以得到一个重要结论
函数
f(z)在一点
z0处解析的充要条件是:它在
z0的某一邻域内有幂级数展开式
f(z)=n=0∑∞an(z−z0)n
这个性质从级数的角度深刻反映了解析函数的本质。
-
函数在 z=0 处的泰勒展开式
ez=n=0∑∞n!1znsinz=n=0∑∞(2n+1)!(−1)nz2n+1cosz=n=0∑∞(2n)!(−1)nz2n1−z1=n=0∑∞zn(1+z)21=n=0∑∞(−1)n−1nzn−1(z∈C)(z∈C)(z∈C)(∣z∣<1)(∣z∣<1)
Ln (1+z)的主值支
ln(1+z)=n=0∑∞n+1(−1)nzn+1(∣z∣<1)
(1+z)α的主值支
eαln(1+z)=1+αz+(2α)z2+⋯+(nα)zn+⋯(∣z∣<1)
其中
(nα)=n!α(α−1)⋯(α−n+1)
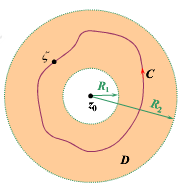
洛朗级数(Laurent Series)
-
洛朗级数(Laurent Series):称形如
n=−∞∑+∞an(z−z0)n=⋯+a−n(z−z0)−n+⋯+a−1(z−z0)−1+a0+a1(z−z0)+⋯+an(z−z0)n+⋯的级数称为洛朗级数,其中
z0,an(n∈Z)为复常数。
洛朗级数由正幂次项
n=0∑∞an(z−z0)n和负幂次项
n=−1∑−∞an(z−z0)n组成,分别称为洛朗级数的解析部分和主要部分。若解析部分和主要部分在点
z=ξ收敛,则洛朗级数在点
z=ξ收敛。
-
收敛圆环(ring of convergence):显然洛朗级数的收敛域是解析部分和主要部分收敛域的交集。
(1) 对于解析部分,设其收敛半径为R,其收敛圆域为
∣z−z0∣<R
(2) 对于主要部分,令
ξ=(z−z0)−1,并令
bn=a−n,则级数变形为ξ的幂级数
n=1∑∞bnξn,设它的收敛半径为
R1,其收敛圆域为
∣ξ∣<R1
于是对于洛朗级数主要部分,当
∣z−z01∣<R1即
∣z−z0∣>R11 时收敛。
(3) 令
r=R11,由上面的讨论可知
若
r<R,则洛朗级数的收敛域为
r<∣z−z0∣<R,此圆环称为收敛圆环。且知它在该圆环内绝对收敛,在闭圆环
r<r′⩽z−z0⩽R′<R上一致收敛。
-
洛朗定理:设
f(z)在圆环域
D:R1<∣z−z0∣<R2 内解析,则
f(z)在此圆环内一定能展开为
f(z)=n=−∞∑+∞an(z−z0)n ,并且系数
an被
f(z)及圆环唯一确定。
其中
an=2πi1∮C(ξ−z0)n+1f(ξ)dξ(n∈Z) ,C为此圆环内围绕
z0的任何一条正向简单闭曲线,此公式称为洛朗展开式(Laurent expansion)。
实例
- 求函数
f(z)=(z−1)(z−2)1分别在下列圆环的洛朗展开式
(1) 0<∣z∣<1;(2) 1<∣z∣<2;(3) 2<∣z∣<+∞
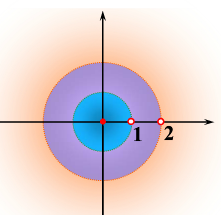
解:部分分式分解
f(z)=1−z1−2−z1
(1) 在
0<∣z∣<1中有
∣z∣<1,∣2z∣<1,由上一章的实例知
1−z1=n=0∑∞zn;2−z1=n=0∑∞2n+1zn
于是
f(z)=n=0∑∞zn−n=0∑∞2n+1zn=n=0∑∞(1−2n+11)zn
上述结果中不含 z 的负幂项,原因在于
f(z)在
z=0处解析。
(2) 在
1<∣z∣<2中有
∣z1∣<1,∣2z∣<1,由上一章的实例知
1−z1=−n=0∑∞zn+11;2−z1=n=0∑∞2n+1zn
于是
f(z)=−n=0∑∞zn+11−n=0∑∞2n+1zn
(3) 在
2<∣z∣<+∞ 中有
∣z1∣<1,∣z2∣<1,由上一章的实例知
1−z1=−n=0∑∞zn+11;2−z1=−n=0∑∞zn+12n
于是
f(z)=n=0∑∞zn+12n−1
- 求函数在
f(z)=zsinz在
0<∣z∣<∞的洛朗展开式
f(z)=zsinz=z1n=0∑∞(2n+1)!(−1)nz2n+1=n=0∑∞(2n+1)!(−1)nz2n
- 计算
∮Cez1dz,其中C 为正向圆周
∣z∣=1
由于
ez1=1+z1+2!z21+⋯+n!zn1+⋯
在洛朗展开式的系数中,在
n=−1时,有
a−1=2πi1∮Cf(z)dz
于是有
∮Cez1dz=2πi
孤立奇点(Isolated Singular Point)
孤立奇点:设函数
f(z) 在
z0不解析,但在
z0的某个去心邻域
0<∣z−z0∣<R内解析,则称点
z0为函数
f(z) 的孤立奇点(isolated singular point)。
-
孤立奇点的类型:设点
z0为函数
f(z)的孤立奇点
(1) 若
f(z) 在点
z0的洛朗级数的主要部分为零,则称点
z0为
f(z) 的可去奇点(removable singularity);
(2) 若
f(z) 在点
z0的洛朗级数的主要部分有限多项,即存在正整数m,
a−m=0,当
n<−m,an=0,则称点
z0为
f(z) 的m级(阶)极点(m-order pole);
(3) 若
f(z) 在点
z0的洛朗级数的主要部分有无限多项,则称点
z0为
f(z) 的本性奇点(essential singularity)
依定义,
z=0是
zsinz的可去奇点,
z=0是
z2sinz的一阶极点,
z=0是
ez1的本性奇点。
-
孤立奇点类型判定
可去奇点判定:设点
z0为函数
f(z)的孤立奇点,则下列三个条件是等价的:
(1) 点
z0为
f(z)的可去奇点;
(2)
z→z0limf(z)=C0,其中
C0为一复常数;
(3) 函数
f(z)在点
z0的某个去心邻域内有界。
m 阶极点判定:
z0为函数
f(z)的m阶极点的充要条件是
f(z)=(z−z0)m1φ(z),其中
φ(z)在
z0解析且
φ(z0)=0
极点判定:
z0为函数
f(z)的极点的充要条件是
z→z0limf(z)=∞
本性奇点判定:
z0为函数
f(z)的本性奇点的充要条件是
z→z0limf(z)不存在,也不趋于∞
本性奇点判定 2:若点
z0为
f(z)的本性奇点,且
z→z0limf(z)=0,则点
z0必为
f(z)1的本性奇点。
-
函数的零点与极点的关系
定理 1:若
z0是
f(z)的m级极点,则
z0是
f(z)1的m级零点,反之亦然。
定理 2:设
z0分别是函数
φ(z),ψ(z)的m级零点和n级零点,
f(z)=ψ(z)φ(z),则有
(1) 当
m>n 时,
z0是
f(z)的
m−n级零点;
(2) 当
m<n 时,
z0是
f(z)的
n−m级零点;
(3) 当
m=n 时,
z0是
f(z)可去奇点。
- 函数在无穷远点的性质
在扩充复平面上讨论函数的奇点,若无特殊声明,则约定无穷远点 ∞为任意函数的奇点。
定义 1:设函数
f(z)在无穷远点的邻域
r<∣z∣<+∞内解析,则无穷远点∞就称为函数
f(z)的孤立奇点。
函数在无穷远点的洛朗级数
设
ξ=0是
h(ξ)的孤立奇点,则有
h(ξ)=n=−∞∑+∞bnξn=n=0∑∞bnξn+n=1∑∞b−nξ−n(0<∣ξ∣<r1)
若令
ξ=z1,则有
f(z)=h(z1)=n=0∑∞bnz−n+n=1∑∞b−nzn(r<∣z∣<+∞)
若再令
an=b−n(n∈Z),则有
f(z)=n=0∑∞a−nz−n+n=1∑∞anzn(r<∣z∣<+∞)
称此级数为
f(z)在点
z=∞的洛朗级数,称其中的级数
n=1∑∞anzn为主要部分,级数
n=0∑∞a−nz−n为解析部分。
注意:与函数
f(z)在有限远点的情况相反,函数
f(z)在无穷远点的罗朗级数的解析部分是由非正幂项组成,而主要部分是由正幂项组成。
定义 2:设
h(ξ)=f(ξ1),如果
ξ=0是
h(ξ)的可去奇点、m级极点或本性奇点,则称
z=∞是
f(z)的可去奇点、m级极点或本性奇点。
无穷远点孤立奇点的分类:设点
z=∞为函数
f(z)的孤立奇点,若函数在
z=∞处的洛朗级数
(1) 不含正幂项,则无穷远点
z=∞是
f(z)的可去奇点;
(2) 含有有限个正幂项,且
zm为最高正幂,则无穷远点
z=∞是
f(z)的m阶奇点;
(3) 含有无穷多正幂项,无穷远点
z=∞是
f(z)的本性奇点。
留数(Residue)
留数的概念与计算
-
引述:当函数
f(z)在邻域
∣z−z0∣<δ内解析时,由柯西-古萨特定理知
∮Cf(z)dz=0,其中C是该邻域内围绕
z0的任何一条正向简单闭曲线。
但是,如果
z0是一个孤立奇点,则积分一般不等于零。设
f(z)在
z0去心领域
0<∣z−z0∣<δ内的洛朗展开式为
f(z)=n=−∞∑+∞an(z−z0)n,对此项逐项积分,利用前一章实例的结果
∮C(z−z0)ndz={2πi,0,n=−1n=−1,n∈Z,可以得到
∮Cf(z)dz=2πia−1
这表明,
f(z)的洛朗展开式沿围绕孤立奇点的正向简单闭曲线积分后,只留下
(z−z0)的负一次幂,,接下来我们就来研究此系数
a−1
-
留数(Residue)
留数定义:设
z0是
f(z)的孤立奇点,即
f(z)在去心邻域
0<∣z−z0∣<δ内解析,则
f(z)在
z0的洛朗展开式的负一次幂的系数
a−1,称为留数,记作
Res(f,z0),即
Res(f,z0)=2πi1∮Cf(z)dz其中C是该去心邻域内围绕
z0的任何一条正向简单闭曲线。
留数定理:设函数
f(z)在区域D内除有限个孤立奇点
z1,z2,⋯,zn外处处解析,C是D内包围所有奇点的一条正向简单闭曲线,则
∮Cf(z)dz=2πik=1∑nRes(f,zk)
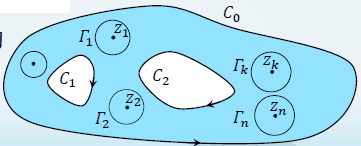
证明:如图,由复合闭路定理有
∮Cf(z)dz=k=1∑n∮Γkf(z)dz=2πik=1∑nRes(f,zk)
-
无穷远点的留数
无穷远点的留数:
Res(f,∞)=2πi1∮C−f(z)dz=−a−1
其中C是围绕原点
z=0的任何一条正向简单闭曲线。
无穷远点留数定理:
k=1∑nRes(f,zk)+Res(f,∞)=0
其中C是围绕原点且包围所有孤立奇点
z1,z2,⋯,zn的一条正向简单闭曲线。
留数的计算
- 如果
z0是
f(z)的可去奇点
Res(f,z0)=0
- 如果
z0是
f(z)的本性奇点,只能用洛朗展开式法求
a−1
- 如果
z0是
f(z)的极点
Res(f,z0)=⎩⎪⎨⎪⎧z→z0lim(z−z0)f(z)(m−1)!1z→z0limdzm−1dm−1[(z−z0)mf(z)]if 1-order poleif m-order pole
- 如果
f(z)=Q(z)P(z),
P(z),Q(z)均在
z0解析,且
P(z0)=0,Q(z0)=0,Q′(z0)=0,则
z0是
f(z)的一阶极点
Res(f,z0)=Q′(z0)P(z0)
- 无穷远点的留数
Res(f,∞)=−Res[f(z1)⋅z21,0]
实例
- 计算积分
∮Cz2−1zezdz,C为正向圆周
∣z∣=2
被积函数有两个一阶极点
±1,而这两个极点都在圆周C内,所以
∮Cz2−1zezdz=2πi[Res(f,1)+Res(f,−1)]=2πi(2e+2e−1)=πi(e+e−1)
- 计算积分
∮Cz(z−1)2ezdz,C为正向圆周
∣z∣=2
被积函数有一个一阶极点
z=0和一个二阶极点
z=1,所以
∮Cz(z−1)2ezdz=2πi[Res(f,0)+Res(f,1)]=2πi
- 求
f(z)=z−1在 ∞ 点的留数
Res(z−1,∞)=−Res[f(ξ1)⋅ξ21,0]=−Res(ξ1,0)=−1
留数在定积分计算中的应用(Application of Residue in Definite Integral)
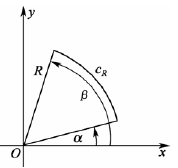
引理 1:设函数
f(z)在闭区域
D={z∣α⩽argz⩽β(0⩽α⩽β⩽π)}上连续,
CR为圆周
C:∣z∣=R 在D内的一段弧,若对
CR上的任意的点 z 均有
z→∞limzf(z)=k,则
R→∞lim∫CRf(z)dz=k(β−α)i
引理 2:设函数
f(z)在闭区域
D={z∣α⩽arg(z−z0)⩽β(0⩽α⩽β⩽π),∣z∣⩽r0}上连续,
Cr为圆周
C:∣z−z0∣=r(r<r0) 在D内的一段弧,若对
Cr的任意的点 z 均有
z→z0lim(z−z0)f(z)=k,则
r→0lim∫Crf(z)dz=k(β−α)i
若尔当(Jordan)引理:设函数
f(z)在闭区域
D={z∣α⩽argz⩽β(0⩽α⩽β⩽π),0<R0⩽∣z∣<+∞}上连续,
CR为圆周
C:∣z∣=R(R>R0) 在D内的一段弧,若对
CR上的任意的点 z 均有
z→∞limf(z)=0,则对于任意
a>0有
R→∞lim∫CRf(z)eiazdz=0
积分计算
-
形如
∫02πR(cosθ,sinθ)dθ 的积分
这里讨论的被积函数
R(cosθ,sinθ)是有理函数
另
z=eiθ,则
dz=ieiθdθ=izdθ
sinθ=2izz2−1,cosθ=2zz2+1
所以
∫02πR(cosθ,sinθ)dθ=∫∣z∣=1R(2zz2+1,2izz2−1)iz1dz
令
f(z)=R(2zz2+1,2izz2−1)iz1,则
∫02πR(cosθ,sinθ)dθ=∮∣z∣=1f(z)dz=2πik=1∑nRes(f,zk)
其中
z0,z1,⋯,zn为在圆周
∣z∣=1内的孤立奇点。
-
形如
∫−∞+∞R(x)dx 的积分
被积函数
R(x)为有理函数,其分母的次数至少比分子的次数高二次,且在实轴上连续,设
R(z)=zm+b1zm−1+⋯+bmzn+a1zn−1+⋯+an,m−n⩾2 为一不可约分式。
由留数定理有
∫−rrR(z)dz+∫CrR(z)dz=2πik=1∑nRes[R(z),zk]
其中
z0,z1,⋯,zn为
Im z>0 内所有的极点
令
r→∞,对上式两端取极限
∫−∞+∞R(z)dz+r→∞lim∫CrR(z)dz=2πik=1∑nRes[R(z),zk]
由于
R(z)分母的次数至少比分子的次数高二次,所以
z→∞limzR(z)=0
由引理 1 知
r→∞lim∫CrR(z)dz=0
所以
∫−∞+∞R(z)dz=2πik=1∑nRes[R(z),zk]
-
形如
∫−∞+∞R(x)eiaxdx(a>0) 的积分
用上例的方法,根据若尔当引理可得
∫−∞+∞R(z)eiaxdz=2πik=1∑nRes[R(z)eiax,zk]
- 实例
(1) 积分
∫0+∞xsinxdx=2π
(2) 积分
∫0+∞(1+x)xadx=sinπaπ(0<a<1)
对数留数与辐角原理(Logarithmic Residue and Argument Principle)
定理 1:设闭曲线C是区域D的边界线,函数
f(z)在D内除极点外每一点都解析,并且在C上解析,则
2πi1∮Cf(z)f′(z)dz=P−N这里P和N分别表示在D内零点及极点的总数, 而且每个k阶零点或极点分别算作k个零点或极点。
上式左端称为函数
f(z)关于围线C的对数留数(Logarithmic Residue),实际上
f(z)f′(z)=dzd[Ln f(z)]。它提供了一种计算复变函数沿围线积分的方法。
辐角原理(Argument Principle):设有闭曲线C及函数
f(z),满足定理 1 的条件,则
P−N=2π1ΔCargf(z) 这里
ΔCargf(z)表示z沿C的正向绕行一周时,函数
f(z) 的辐角改变量。
儒歇定理 (Rouché’s theorem):设C是一围线,若函数
f(z)与
ϕ(z)均在C的内部及C上解析,且满足
∣ϕ(z)∣<∣f(z)∣, z∈C, 则
f(z)+ϕ(z)与
f(z) 在C的内部的零点个数相同(一个k级零点算作k个零点)。
代数基本定理:任何复系数一元n次多项式方程
f(z)=a0zn+a1zn−1+⋯+an(a0=0) 有且只有 n 个零点(n 级零点就算作 n 个零点)。
共形映射(Conformal Mapping)
解析函数的映射性质
导数的几何意义
- 设C 是一条有向光滑曲线,其方程为
z=z(t),a⩽t⩽b,它的正向为随t增大时z的移动方向,设
z0=z(t0),z=z(t0+Δt)=z(t) 为曲线C上的点,则割线
zz0的正向与复数
Δtz(t0+Δt)−z(t0) 表示的向量的方向一致,因此
z′(t0)=Δt→0limΔtz(t0+Δt)−z(t0) 所表示的向量就是曲线C 处的切线向量,且与C的方向一致。
因此在处的切线与实轴的夹角可复数表示为
α=Arg z′(t0)
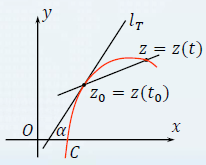
- 设
w=f(z)将曲线C映射成曲线
Γ:w=w(t)=f[z(t)], 则曲线
Γ在
w0=f[z(t0)]处的切线与实轴的夹角为
β=Arg w′(t0)=Arg f′(z0)z′(t0)=Arg f′(z0)+Arg z′(t0)
通过映射
w=f(z),曲线C在
z0处的切线逆时针方向旋转
Arg f′(z0)得到曲线
Γ在
z0处的切线。
由此,称
Arg f′(z0)为映射
w=f(z)在点
z0 处的旋转角(angle of rotation)。易知,旋转角只依赖于点
z0,而与曲线C 的形状和方向无关。称旋转角的这种性质为旋转角不变性。

- 由旋转角不变性立即可获得一个重要性质:对于连续函数
w=f(z),z∈D, 若
f′(z0)=0,则过点
z0 具有切线的任意两条有向连续曲线
C,C1 的夹角(二曲线在点
z0的切线所夹的角)与象曲线在点
w0=f(z0) 的夹角保持大小相等且方向相同(即由原象曲线
C,C1 的旋转方向与由象曲线
Γ,Γ1 的旋转方向是一致的),该性质称为保角性(Conformal)。
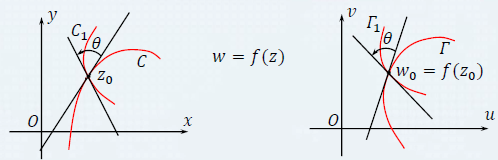
- 由导数定义,有
∣f′(z0)∣=z→z0lim∣z−z0∣∣f(z)−f(z0)∣=r(r=0)
上式表明,像点之间的距离
∣f(z)−f(t0)∣与原像点之间的距离
∣z−z0∣比值的极限为
∣f′(z0)∣,称这个极限为映射
w=f(z)在点
z0 的伸缩率(shrinkage)。显然,这伸缩率只依赖于点
z0 ,而与曲线C 的形状及方向无关,这种性质称为伸缩率不变性。
- 共形映射(conformal mapping)
若函数
w=f(z)在
z0 的邻域内有定义,且在
z0具有保角性和伸缩率不变性,则称映射
w=f(z)在
z0 是共形的,或称
w=f(z)在
z0 是共形映射。若映射
w=f(z)在区域G 内每一点都是共形的,则称该映射为区域G 内的共形映射。
单叶函数 (univalent function):设函数
f(z)在区域D内解析,且对D内任意不同两点
z1和
z2,均有
f(z1)=f(z2) ,则称
f(z)为区域D内的单叶解析函数,简称单叶函数。
由单叶函数的性质知,单叶函数在定义域内为共形映射。
定理 1:设
f(z)在区域D内单叶解析,则
f′(z)=0,z∈D
保域性定理:设函数
f(z)在区域D内解析,并且不恒等于常数,则D的像
D′=f(D)是一个区域,即
f(z)确定从区域D到区域
D′的一个满射。
定理 2:若函数
w=f(z)在
z0 解析,且
f′(z0)=0,则映射
w=f(z)是共形的,而且
Arg f′(z0) 表示这个映射在
z0 的旋转角,
∣f′(z0)∣ 表示这个映射在
z0 的伸缩率。如果解析函数
w=f(z)在G 内处处有
f′(z)=0,则映射
w=f(z)是G 内的共形映射。
定理 3:若函数
w=f(z)为区域G 内单叶函数,则反函数
z=φ(w) 为
G1=f(G) 内单叶函数,并有
φ′(w0)=f′(z0)1,z0∈G,w0=f(z0)∈G1
分式线性映射(Fractional Linear Mapping)
-
分式线性映射:设
a,b,c,d为满足
ad−bc=0的复常数,称由分式线性函数
w=cz+daz+b构成的映射为分式线性映射。特别的,当
c=0时,称为线性映射。
(1) 其中条件限制
ad−bc=0是为了映射的保角性,否则将有
dzdw=(cz+d)2ad−bc=0,此时
w≡ 常数,将会把整个 z平面映射 w平面一个点。
(2) 逆映射
z=cw−a−dw+b满足
(−a)(−d)−bc=0,仍为分式线性映射。
(3) 三个基本映射:一个一般的分式线性映射可以分解为几个简单的映射的复合。
当
c=0 时,有
w=daz+b=da(z+ab)
当
c=0 时,有
w=cz+daz+b=(b−cad)cz+d1+ca
由此可见,分式线性映射可由
w=z+b,w=αz,w=z1 复合而成。
-
平移映射(translation):
w=z+b
-
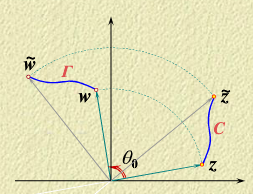
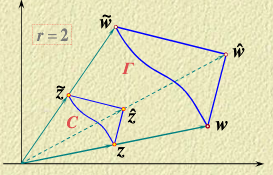
旋转和相似映射(rotation and similar):
w=αz
设
α=reiθ0,z=∣z∣eiθ,则
w=r∣z∣ei(θ0+θ)
从而
Arg w=Arg z+θ,∣w∣=r∣z∣,即 z点先旋转角度
θ0,
∣z∣再伸缩
r 倍。
-
反演映射(inverse):
w=z1
设
z=reiθ,则
w=r1ei(−θ)
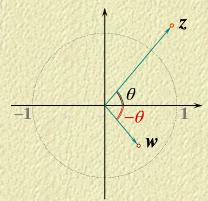
反演映射通常分解为两个映射完成:
(1)
ξ=zˉ1=r1eiθ ,
∣ξ∣∣z∣=1,即
z 和
ξ关于单位圆周
∣z∣=1对称
(2)
w=ξˉ=r1ei(−θ),
ξ 和
w关于实轴对称。
- 分式线性映射的性质
为便于研究分式线性变换在扩充复平面的性质,约定:
(1) 反演映射
w=z1将
z=0映射成
w=∞,
z=∞映射成
w=0
(2) 函数
f(z)在
z=∞及其邻域内的性质可由函数
f(ξ1),ξ=z1在
z=0及其邻域内的性质确定。
(3) 在扩充复平面上将直线视作一个过无穷远点的特殊圆周。
共形性(conformity):分式线性映射在扩充复平面是单叶的,且是共形的。
(1) 线性映射
w=az+b(a=0)是单叶的,且
w′(z)=a=0,显然在扩充复平面是共形的
(2) 反演映射
w=z1是单叶的,且
w′(z)=−z21,根据约定计算,在扩充复平面是共形的
分式线性映射由线性映射和反演映射复合而成,显然是单叶共形的。
保圆性 (circular):分式线性映射将扩充复平面上的圆周映射为圆周。
(1) 线性映射
w=az+b(a=0) 将 z平移,旋转,伸缩,且有相同的旋转角
Arg a和伸缩因子
∣a∣,故将映射成圆。
(2) 反演映射
w=z1,设
z=x+iy,w=u+iv,可得
x=u2+v2u,y=−u2+v2v
对于z平面任意给定的圆
A(x2+y2)+Bx+Cy+D=0,其像曲线满足方程
D(u2+v2)+Bu−Cv+A=0,故仍然为圆。
保对称性(Symmetries):设点
z1,z2是关于圆周C的对称点, 则在分式线性映射
w=f(z)下,他们的像点
w1=f(z1),w2=f(z2)是关于C的像曲线
Γ=f(C) 对称。
定理 1:在扩充复平面上的两点
z1,z2 是关于圆周C 的对称点的充要条件是通过
z1,z2 的任何圆周与圆周C 正交。
对应点公式:若分式性性映射将扩充复平面( z 平面)上3个互异的点
z1,z2,z3 依次映射为扩充复平面(w平面)上的三点
w1,w2,w3,则此分式线性映射就唯一确定,且可写成
w−w2w−w1:w3−w2w3−w1=z−z2z−z1:z3−z2z3−z1
称
z−z2z−z1:z3−z2z3−z1 为
z1,z2,z,z3的交比(cross ratio),或称非调和比,记为
(z1,z2,z,z3)
由上式可知,分式线性函数保持交比不变。
部分初等函数的映射性质
-
指数函数的映射:
w=ez=exeiy ,以
2πi为周期,在一个周期内为单叶函数。
指数函数将水平带状区域映射为角形区域。
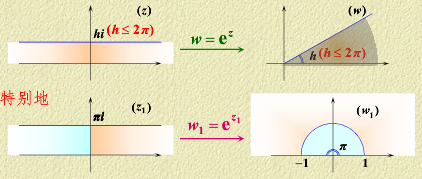
-
对数函数的映射:
w=Ln z=lnz+2kπi,主值分支
lnz=ln∣z∣+iargz
对数函数为指数函数反函数,在单值分支内为单叶函数。
取单值分支
fk(z)=ln∣z∣+iargz+2kπi
设 z平面内角形区域
z=reiθ(0<θ<θ0⩽2π),则
fk(z)=ln∣r∣+i(θ+2kπ)
即将 z平面角形区域映射成 w平面平行于实轴的带形区域.
-
幂函数的映射:
w=zn(n∈Z+)
设
z=reiθ,则
w=rneinθ ,即
∣w∣=rn,argw=nθ
即 z平面角形区域
argz∈[0,θ0] 映射为 w平面角形区域
argw∈[0,nθ0]
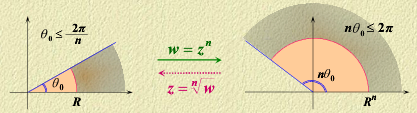
共形映射的基本问题示例
共形映射的基本问题是:对任意给定的两个单连通区域G 与G′ ,是否存在一个单叶函数能将G 保形映射成G′ = f(G)?若存在,是否唯一。
黎曼(Riemann)定理:若G 为扩充复平面上的一个单连通区域,其边界点不止一点,则必存在单叶函数
w=f(z) 将G映射为单位圆D;若G内某一点满足条件
f(z0)=0且
f′(z0)>0,则映射
w=f(z) 是唯一的。
边界对应定理(boundary correspondence):设 C为单连通区域G的边界,若函数
w=f(z) 在闭区域
Gˉ=G∪C上解析,且把
C双射成
C1,则函数
w=f(z) 在G内部单叶,且把G映射成
C1包围的区域
G1
边界对应定理,将区域问题变为考查察边界问题。
-
将上半平面(半径为无穷大的圆)
Im z>0 映射为单位圆盘
∣w∣<1 的分式线性映射。
解:设 z上平面一点
z=z0(Im z0>0)映射到 w平面原点
w=0,有保对称性知,
z=zˉ0将映射成
w=∞,故可设线性映射
w=kz−zˉ0z−z0,k∈R
只须利用该映射将实轴上的点 z = x 映射为单位圆周
∣w∣=1上的点,即当z = x时,有
∣w∣=∣kx−zˉ0x−z0∣=∣k∣∣x−zˉ0x−z0∣=∣k∣=1,即
k=eiθ,θ∈R
所求的映射为
w=eiθz−zˉ0z−z0(θ∈R,Im z0>0)
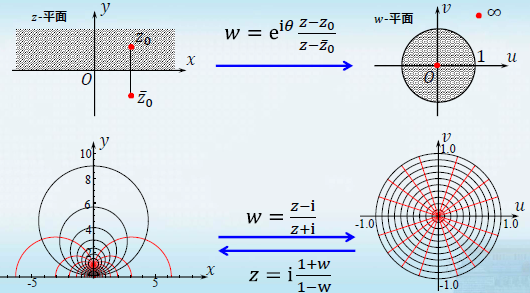
-
求把圆盘
∣z∣<1 映射成
∣w∣<1 的分式线性映射。
解:设 z上平面一点
z=z0(∣z0∣<1)映射到 w平面原点
w=0,有保对称性知,
z=z0关于圆周
∣z∣=1 的对称点
zˉ01 将映射成
w=∞,故可设线性映射
w=kz−zˉ01z−z0=k′1−zˉ0zz−z0,k′=kzˉ0
只须利用该映射将
∣z∣=1 映射为
∣w∣=1上的点,即当z = 1时,有
∣w∣=∣k′1−zˉ01−z0∣=∣k′∣=1,即
k′=eiθ,θ∈R
所求的映射为
w=eiθ1−zˉ0zz−z0(θ∈R,∣z0∣<1)
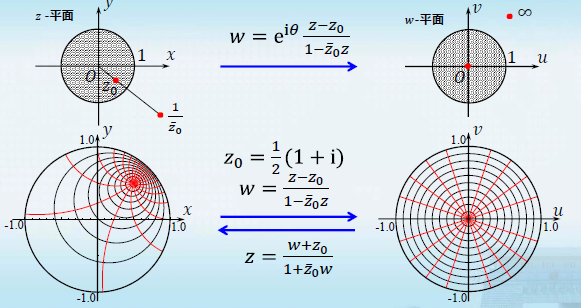
-
将角形区域
G:0<argz<π/6映射为单位圆盘
∣w∣<1的映射
z1=z6可将角形区域映射成半平面
G1:Im z1>0
又根据上述例 1,取
z0=i,θ=0,通过
w=z1+iz1−i将
G1映射成单位圆盘
复合可得
w=z6+iz6−i
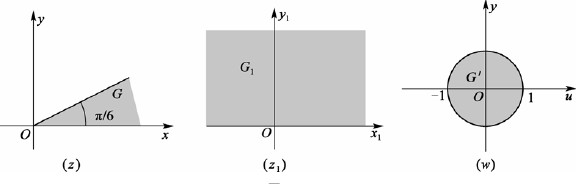
-
将半圆
G:∣z∣<1,Im z>0 映射成上平面
G′:Im w>0的映射
w=(z−1z+1)2
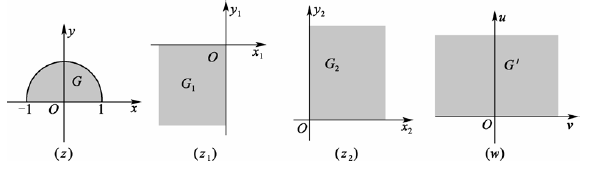
-
将上半平面(半径为无穷大的圆)
G:Im z>0 映射为一般圆盘
G′:∣w−w0∣<R
首先
G 经
z1=eiθz−zˉ0z−z0映射为
G1:∣z1∣<1
齐次
G1经
w=Rz1+w0映射为
G′:∣w−w0∣<R
复合可得
z1=Reiθz−zˉ0z−z0+w0(θ∈R,Im z0>0)
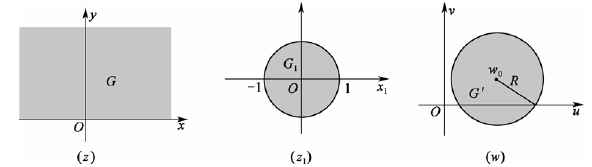
-
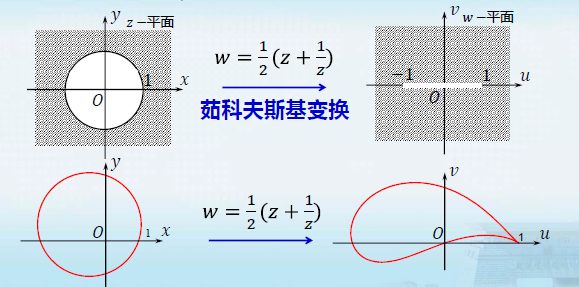
茹科夫斯基(Zhukovskii)映射:
w=21(z+z1)
(1) 将圆周
∣z∣=r>1映射为椭圆周
令
z=reiθ,w=u+iv,则
{u=21(r+r1)cosθv=21(r−r1)sinθ
像的坐标满足方程
a2u2+b2v2=1,其中
a=21(r+r1),b=21(r−r1)
即焦点为
(−1,0),(1,0)的椭圆
(2) 把扩充 z平面的单位圆外部
∣z∣>1映射成扩充 w平面去掉割线
[−1,1]的平面
可将单位圆外部视为无穷个圆周
∣z∣=r>1的集合,只须确
定这无穷个圆周的象即。
基于(1) 的讨论,知道这无穷个圆周的象是无穷个椭圆周,并且
r→1lim21(r+r1)=1,r→1lim21(r−r1)=0,即椭圆周的长半轴趋向1,而短半轴趋向0,因而相应的椭圆周便退化为w 平面上的线段
[−1,1]
又
r→+∞lim21(r+r1)=+∞,r→+∞lim21(r−r1)=+∞,故能扫过除
[−1,1]外的整个 w平面。