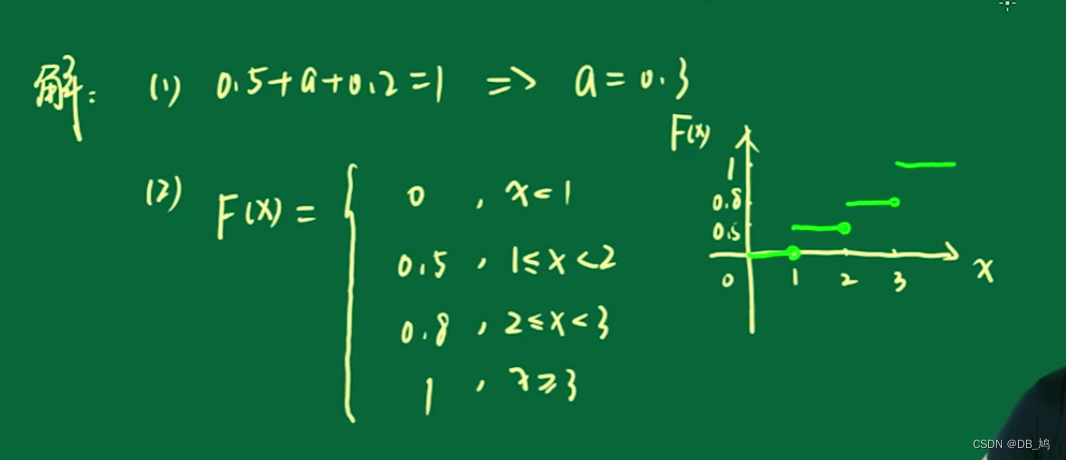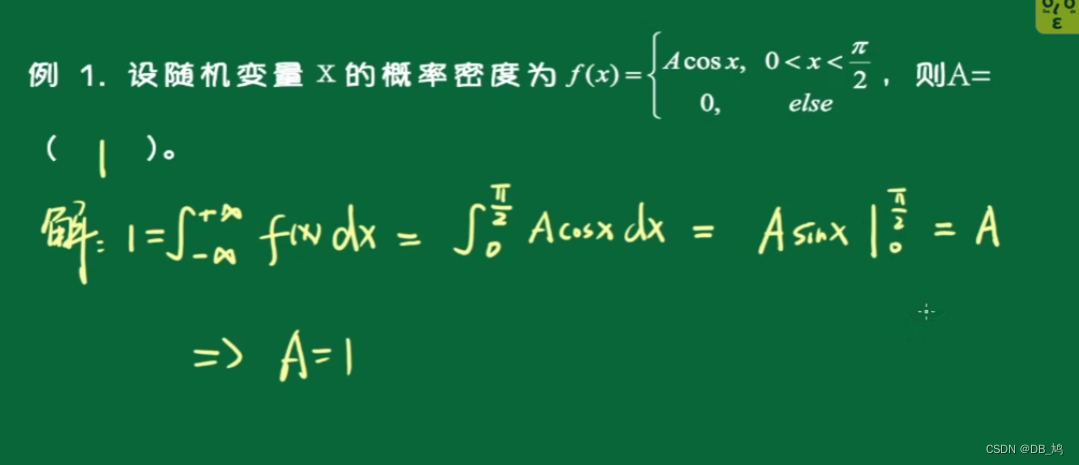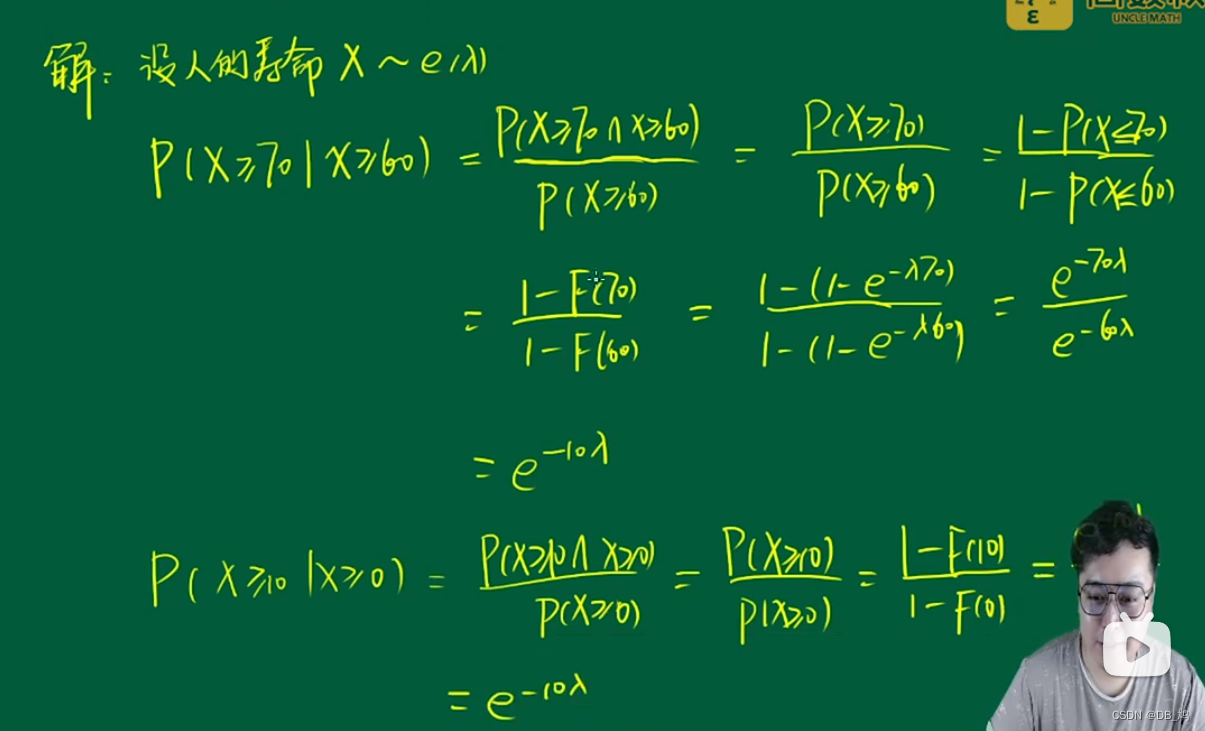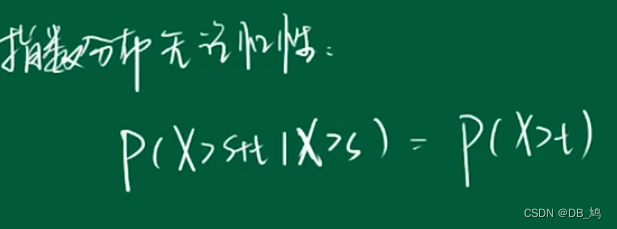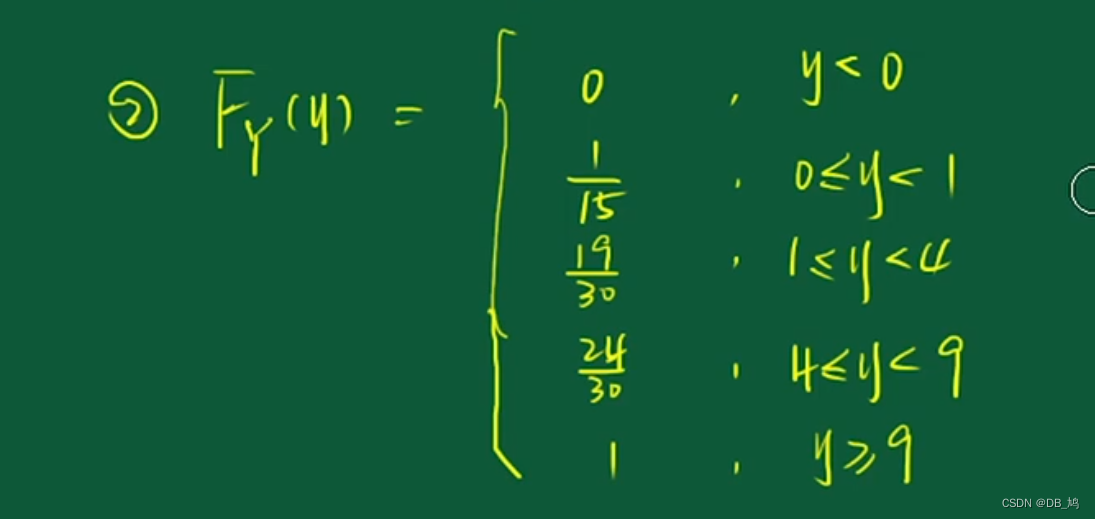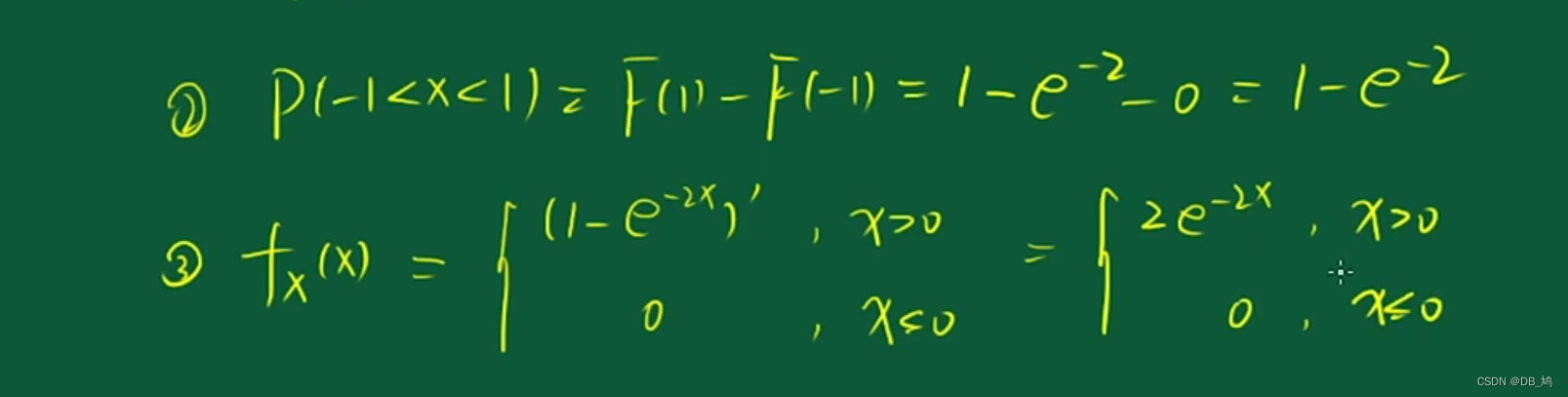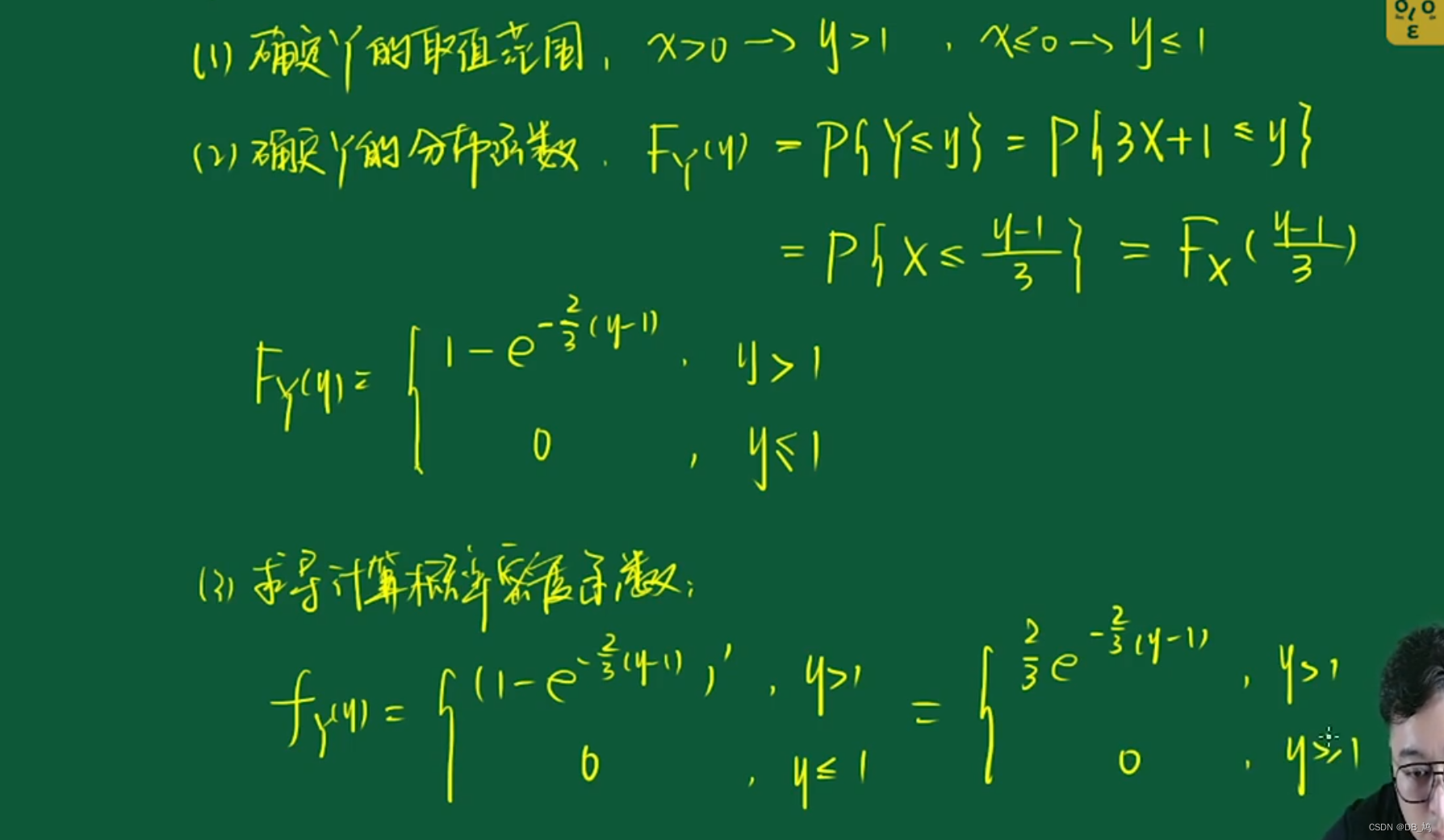概率论与数理统计---随机变量的分布

一维离散型随机变量

基本概念

随机变量

随机变量就是随机事件的数值体现。

例如投色子记录色子的点数，记录的点数其实就是一个随机变量，他是这个点数出现的数值体现。

注意：

• 随机变量X = X(e) , 是一个单实值函数，每个随机事件的结果只能对应一个随机变量。
• X(e)体现的是对随机事件的描述，本质上也是随机事件。
• X(e)的各个取值都有一定的概率。
• 在进行实验之前知道X(e)可能会有哪些取值，并且每种取值都有可能出现。

离散型随机变量

随机变量分为两种：连续型和离散型，跟函数的连续和间断类似。

• 连续型有无穷多个，不能列举
• 离散型可以一一列举出来，也可以是无限个，但是跟自然数能够一一对应

分布律

随机变量的各个取值对应的概率称为分布律，可以作为计算公式
一般会用一个表格来表示

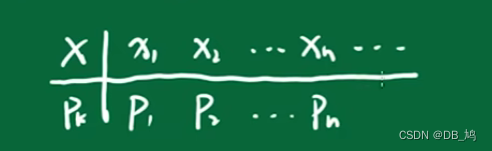
注意：

• 所有的概率都在0-1之间
• 所有概率的和为1

常见的离散型随机变量分布

0-1分布

实验只有两种结果，取值用0和1表示
分布律为：

X	0	1
P	p	1-p

二项分布

对一个只有$A和\bar{A}$的事件进行n次实验，事件发生的次数服从二项分布
用表示$B(n,p)$，事件不发生的概率为$1-B(n,p)$
分布律：$P(n,p)=C_n^k\ast p^k\ast (1-p{)}^{n-k}$(k为事件发生的次数)

泊松分布

泊松分布用于描述一定事件或者空间中事件发生次数的概率，用$\Pi (\lambda )$表示（$\lambda$为该时间或空间内事件发生的平均次数。）
分布律：
$P(X=k)=\frac{{\lambda }^k{e}^{-\lambda }}{k!}$

泊松分布例题

泊松定理

当二项分布B(n,p)的n较大，且p较小时，二项分布大致服从泊松分布Π(np)

即$P(X=k)=C_n^k{p}^k(1-p{)}^{n-k}=\frac{(np{)}^k{e}^{-np}}{k!}$

泊松定理例题

离散型随机变量分布函数

注释：

• F(x)是一个不减函数
• P{a < x <= b} = F(b) - F(a)
• 0 <= F(x) <= 1, F(-00) = 0, F(+00) = 0
• F(x) 是右连续的

随机变量函数的例题

一维连续型随机变量

基本概念

概率密度和概率密度函数

对于连续型随机变量，研究单点没有意义，一般都是研究一个区域对应的概率密度，区域与概率密度的对应关系就是概率密度函数。

概率的密度就是曲线对应的面积（定积分）
注意：

• 概率密度 大于等于 0
• 取值范围为 负无穷 到 正无穷
• 整个概率密度为1

分布函数

与离散型随机变量分布函数对应，概念相同

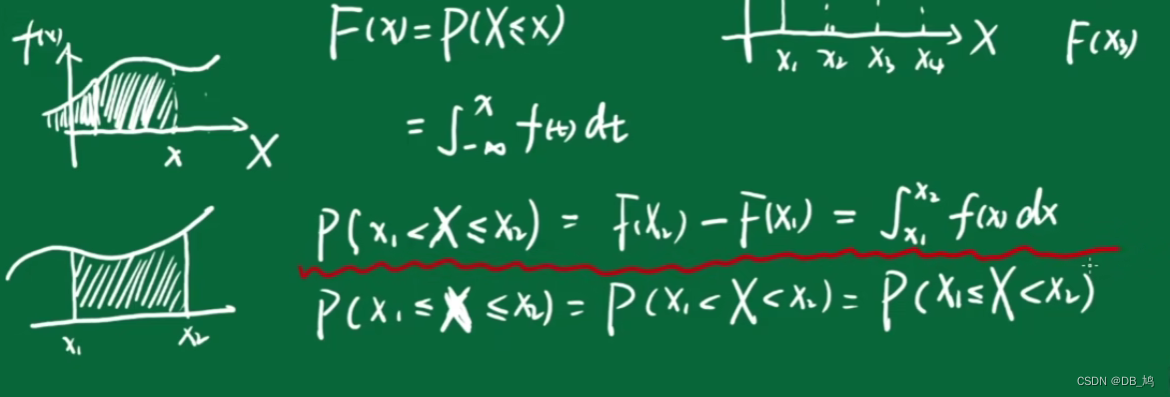
注意连续型随机变量不关注单点问题，只研究某个区域。

例题

常用连续型随机变量分布

均匀分布

U(a,b)

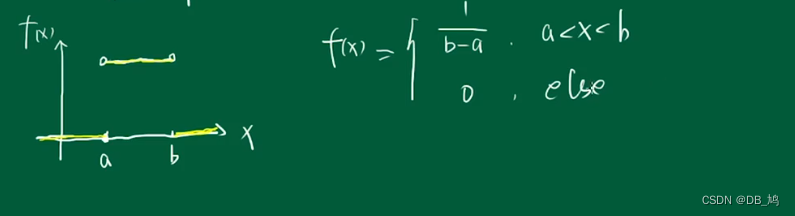
指数分布

e($\lambda$)
事件下一次发生的间隔时间的概率

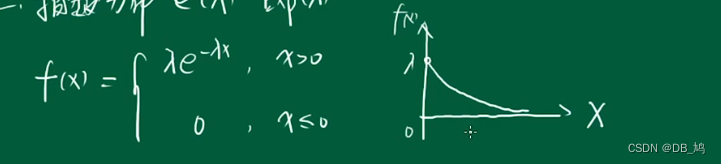
分布函数

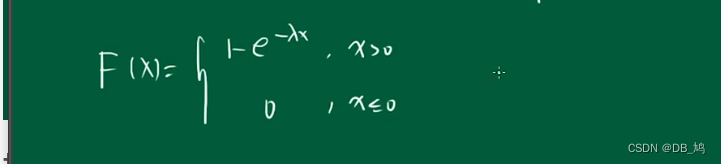
例题

上面的例题说明指数分布具有无记忆性。

正态分布

$N(\mu ,{\sigma }^2)$，也叫高斯分布

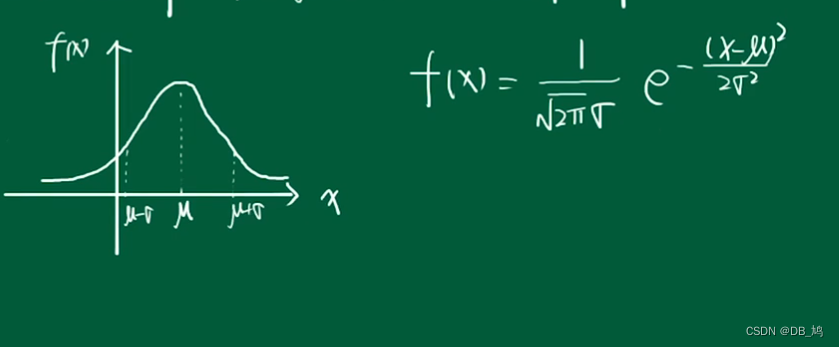
性质：

• 关于x = $\mu$对称。
• 在$x=\mu$处取得最大值。
• 当$x<\mu$时单调递增，当$x>\mu$时单调递减。
• 在$x=\mu \pm \sigma$时有拐点
• y = 0 是水平渐近线

标准正态分布 $N(0,1)$

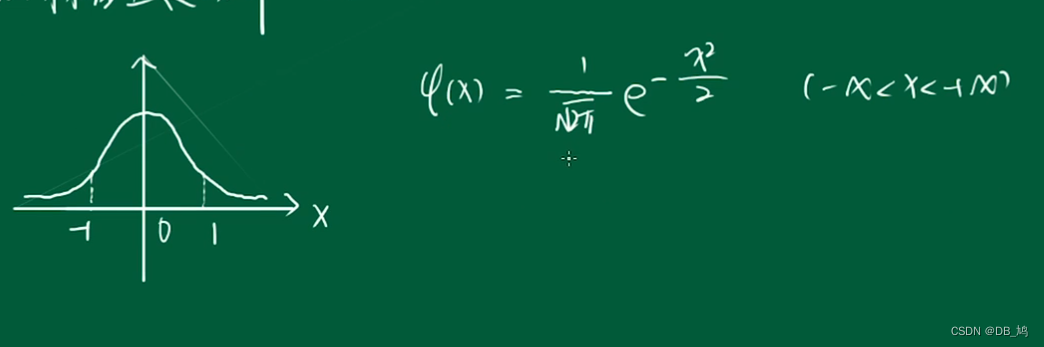
标准正态分布的性质

• 偶函数
• 分布函数$F(-x)=1-F(x)$
• 若X～$N(\mu ,\sigma )$，则$Z=\frac{X-\sigma }{\mu }$ ~ N(0,1);
• 
• 

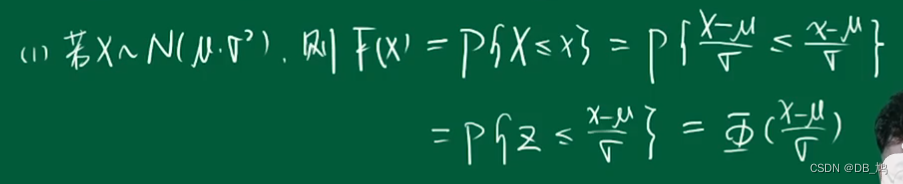
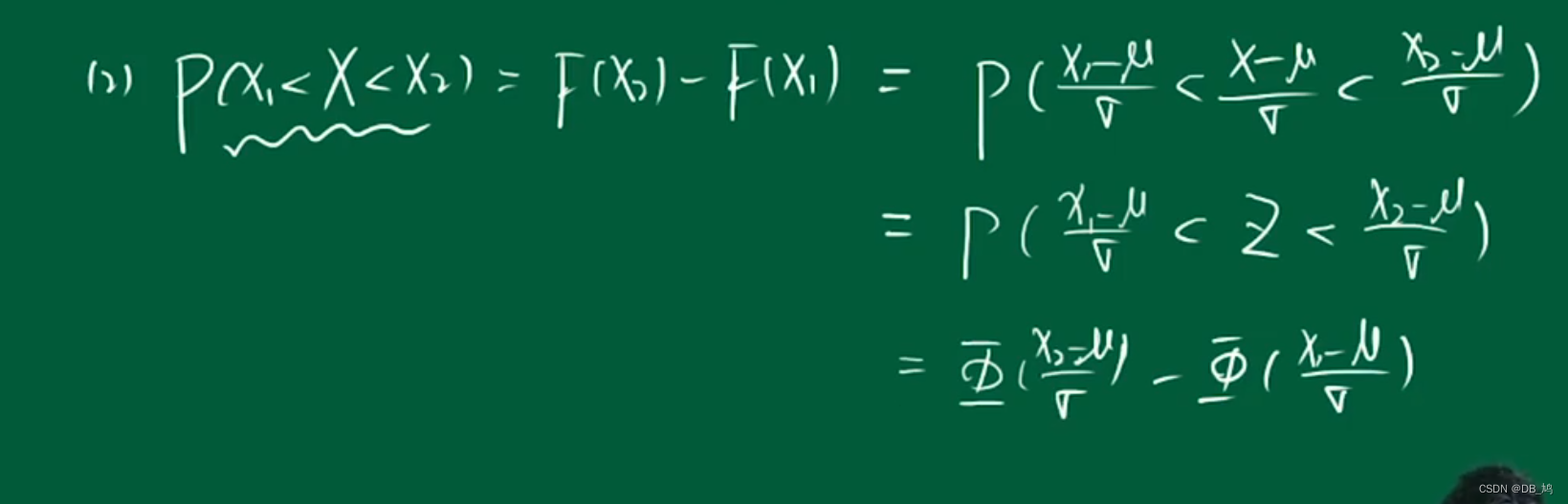
概念不好懂，直接看例题

随机变量函数的分布

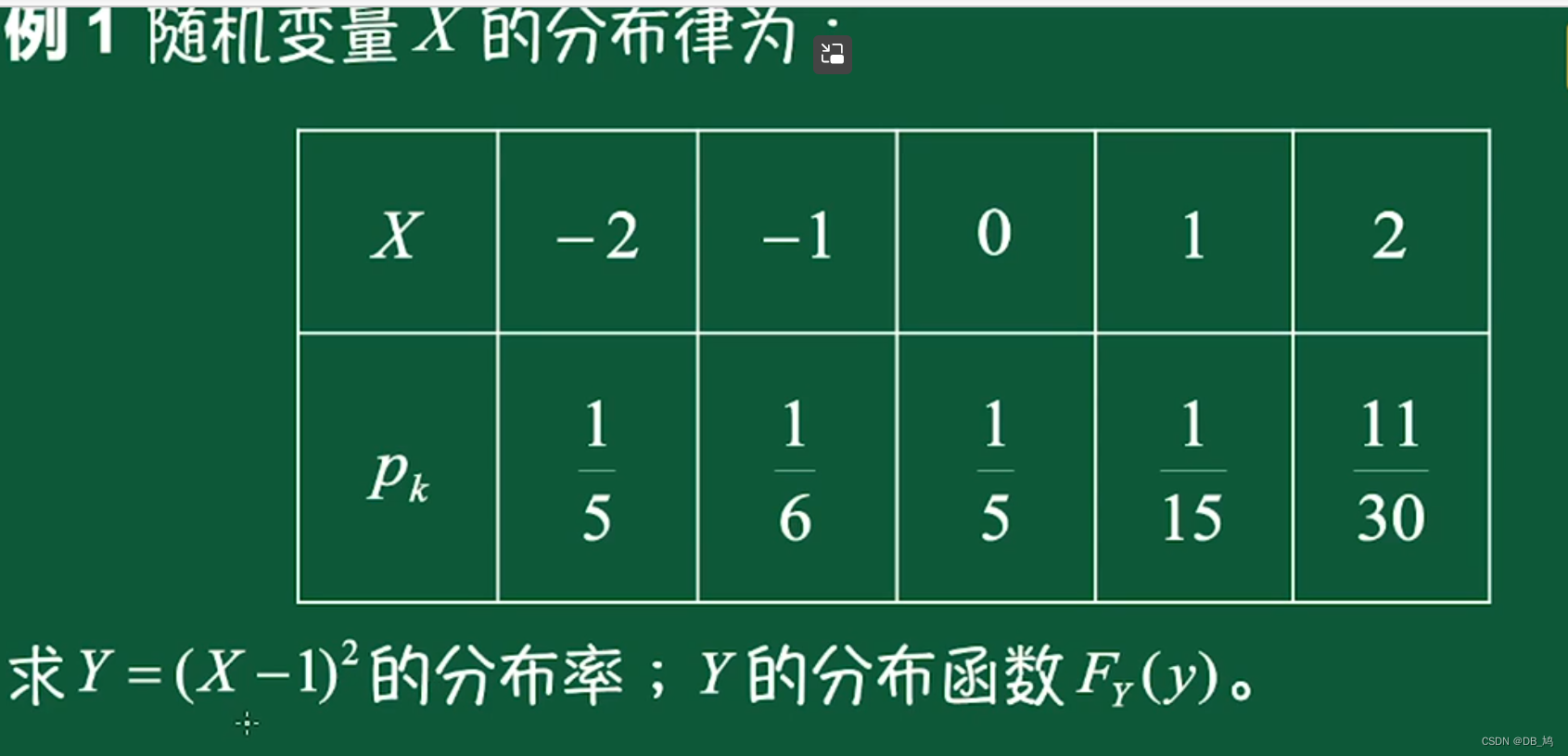
例1

回忆：
分布函数的性质

例2

概率密度函数都是分布函数求导得到的。