大二下:概率论与数理统计复习 导航页:https://blog.csdn.net/COCO56/article/details/100152856
1. 随机变量
随机变量X是一个函数机器,它可以将随机试验的每一个结果e都变成一个单实数X(e):
将试验结果数值化。

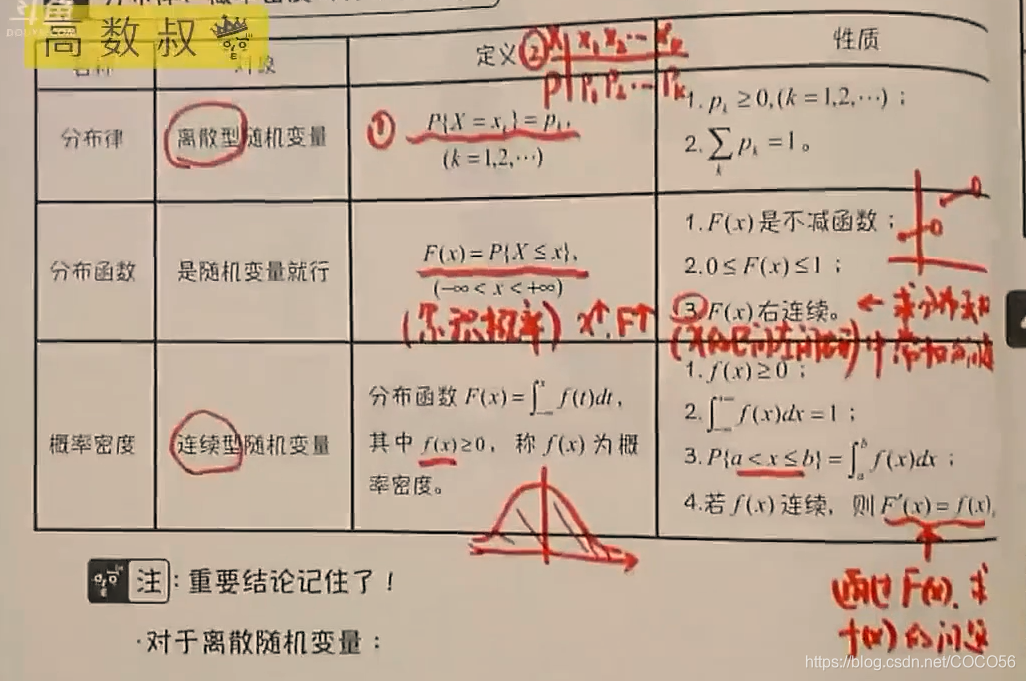
2. 分布律、概率密度与分布函数
| 名称 |
对象 |
定义 |
性质 |
| 分布律 |
离散型随机变量 |
P{X=xk}=pk,(k=1,2,...) |
1.pk≥0,(k=1,2,...);2.k=1∑∞pk=1. |
| 分布函数 |
是随机变量就行 |
F(x)=P{X≤x},(−∞<x<+∞) |
1.F(x)是不减函数;2.0≤F(x)≤1;3.F(x)右连续。 |
| 概率密度 |
连续型随机变量 |
分布函数F(x)=∫−∞xf(t)dt,其中f(x)≥0,称f(x)为概率密度。 |
1.f(x)≥0;2.∫−∞+∞f(x)dx=1;3.P{a<x≤b}=∫abf(x)dx;4.若f(x)连续,则F′(x)=f(x). |
2.1. 重要结论
- 对于离散随机变量
P{a<X≤b}=F(b)−F(a)(1)
P{X>a}=1−F(a)(2)
- 对于连续随机变量
单点概率为0:P{X=a}=0(3)
P{a<X≤b}=P{a≤X≤b}=P{a<X<b}=F(b)−F(a)(4)
P{X>a}=1−F(a)(5)
3. 常用的离散型随机变量
| 名称 |
符号 |
分布律 |
说明 |
|
0−1分布 |
B(1,p) |
P{X=1}=p,P{X=0}=1−p,(0<p<1) |
只有两个可能结果0和1,比如抛硬币,产品是否合格等。 |
|
二项分布 |
B(n,p)n表示实验次数p表示每次发生的概率n次中发生的次数 |
P{X=k}=Cnkpkqn−k,(0<p<1,q=1−p,k=0,1,2,...) |
n重伯努利试验中A发生的次数服从二项分布,表示一系列试验中A发生的次数,比如抛n次硬币正面出现的次数。 |
|
泊松分布 |
P(λ) |
P{X=k}=k!λke−λ,(λ>0,k=0,1,2,...) |
表示一段时间间隔或一定范围内A发生的次数服从泊松分布,比如加油站一小时内来的汽车数量,一天内一个路段发生交通事故的次数等。 |
4. 常用的离散型随机变量
设X服从二项分布B(n,p), 当n较大, p较小时, X近似服从泊松分布P(np), 即
P{X=k}=Cnkpkqn−k≈k!(np)ke−np,
这个定理在二项分布计算中,当遇到n很大,p很小,不好计算时,可以用泊松分布近似计算。
5. 常用的连续型随机变量
| 分布名称 |
表示符号 |
概率密度函数 |
图像 |
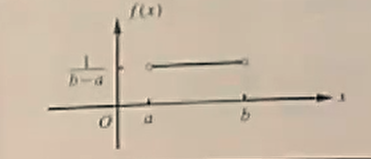
| 均匀分布 |
U(a,b) |
f(x)=⎩⎨⎧b−a1,0,a<x<b其他 |
 |
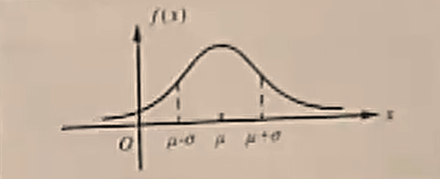
| 正态分布 |
N(μ,σ2) |
f(x)=2π
σ1e−2σ2(x−μ)2(−∞<x<+∞) |
 |
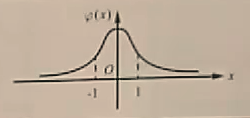
| 标准正态分布 |
N(0,1) |
ϕ(x)=2π
1e2x2(−∞<x<+∞) |
 |
| 指数分布 |
e(λ) |
f(x)={λe−λx,0,x>0x≤0 |
 |
注:
设随机变量
X∼N(μ,σ2),则:
-
其概率密度曲线关于直线x=μ对称,当x<μ时单调上升,当x>μ时单调下降,当x=μ处取得最大值;在x=μ±σ处有拐点;并且以y=0为水平渐近线;
-
Z=σX−μ∼N(0,1),也就是对于一个本身服从正态分布
N(μ,σ2)的随机变量
X,如果对每个取值都减掉
μ再除以
σ,则变化后的随机变量
Z服从标准正态分布
N(0,1)。其概率密度
f(−x)=f(x),分布函数
Φ(−x)=1−Φ(x)。并且:
P{x1≤X≤x2}=F(x2)−F(x1)=Φ(σx2−μ)−Φ(σx1−μ);F(x)=P{X≤x}=P{σX−μ≤σx−μ}=Φ(σx−μ);P{X>x}=P{σX−μ>σx−μ}=1−Φ(σx−μ)
指数分布的概率分布函数:
F(x)=1−e−λx
6. 考点
- 理解分布函数
F(x)=P{X≤x},(−∞<x<+∞)的概念及性质,会计算与随机变量有关的事件的概率。
- 理解离散型随机变量及其概率分布的概念,掌握0-1分布、二项分布、泊松分布及其应用。
- 了解泊松定理的结论和应用条件,会用泊松分布近似表示二项分布。
- 理解连续型随机变量及其概率密度的概念,掌握均匀分布、正态分布、标准正态分布、指数分布及其应用。
- 回球以为随机变量函数的分布。







