前言
想写两篇关于AVL树和B树的较为详细的介绍,发现需要先介绍二叉搜索树作为先导。
定义
二叉搜索树(Binary Search Thee, BST),也被称为二叉排序树(Binary Sort Tree, BST),无论哪种定义,都能表明其特点:有序,能够用于快速搜索。个人更倾向于称其为二叉搜索树。
二叉搜索树,指的是这样的一颗二叉树:一个节点的左子节点小于(小于等于,如果允许存在相等元素的话)它,右子节点大于它。同样地道理适用于其左子树和右子树。
来源
之所以有二叉搜索树,是为了搜索方便。对于n个节点,一般情况下仅需要 的事件就能确定是否存在目标值。当然最坏情况下,二叉树会退化为链表(比如只有左子树),因此,对一个二叉搜索树进行自平衡是很重要的一部分内容,也就是所谓的AVL树,有时候也被称为平衡二叉搜索树。详见“树”据结构二:AVL树。
算法
(由于主要想写的是AVL树和B树,二叉搜索树的算法这里不详细介绍了,哪天有阳光了再好好写写。)
数据结构
class Node<T extends Comparable<T>> {
protected T id = null;
protected Node<T> parent = null;
protected Node<T> lesser = null;
protected Node<T> greater = null;
/**
* Node constructor.
*
* @param parent
* Parent link in tree. parent can be NULL.
* @param id
* T representing the node in the tree.
*/
protected Node(Node<T> parent, T id) {
this.parent = parent;
this.id = id;
}
/**
* {@inheritDoc}
*/
@Override
public String toString() {
return "id=" + id + " parent=" + ((parent != null) ? parent.id : "NULL") + " lesser="
+ ((lesser != null) ? lesser.id : "NULL") + " greater=" + ((greater != null) ? greater.id : "NULL");
}
}二叉搜索树的节点比较简单,最基础的是记录其节点的值、左子节点、右子节点。当然,在实现的时候往往还保留父节点,这会给一些处理带来很大的便利。
查
/**
* Locate T in the tree.
*
* @param value
* T to locate in the tree.
* @return Node<T> representing first reference of value in tree or NULL if
* not found.
*/
protected Node<T> getNode(T value) {
Node<T> node = root;
while (node != null && node.id != null) {
if (value.compareTo(node.id) < 0) {
node = node.lesser;
} else if (value.compareTo(node.id) > 0) {
node = node.greater;
} else if (value.compareTo(node.id) == 0) {
return node;
}
}
return null;
}二叉搜索树最重要的就是查。可以采用递归式查询和非递归式查询(一般用队列实现)。这里使用的是非递归方式。
遍历
二叉搜索树的便利有三种方式:
- 前序遍历:per-order,即根在前,然后左,最后右;
- 中序遍历:in-order,即左在前,根在中,最后有。之所以称其为in-order(按序),是因为对于一个二叉搜索树来说,中序遍历就是按照其节点值的大小顺序遍历;
- 后序遍历:post-order,即左在前,然后右,最后根。
所以遍历的命名方式其实就是看中间节点到底是“前”、“中”还是“后”被访问。
增
/**
* Add value to the tree and return the Node that was added. Tree can
* contain multiple equal values.
*
* @param value
* T to add to the tree.
* @return Node<T> which was added to the tree.
*/
protected Node<T> addValue(T value) {
Node<T> newNode = this.creator.createNewNode(null, value);
// If root is null, assign
if (root == null) {
root = newNode;
size++;
return newNode;
}
Node<T> node = root;
while (node != null) {
if (newNode.id.compareTo(node.id) <= 0) {
// Less than or equal to goes left
if (node.lesser == null) {
// New left node
node.lesser = newNode;
newNode.parent = node;
size++;
return newNode;
}
node = node.lesser;
} else {
// Greater than goes right
if (node.greater == null) {
// New right node
node.greater = newNode;
newNode.parent = node;
size++;
return newNode;
}
node = node.greater;
}
}
return newNode;
}增加一个节点也比较简单,关键是跟节点进行比较,找到应该添加的位置(找到null为止),然后归位(调整一下几个指针的指向)即可。
删
删节点值得好好说一说。当删除一个节点的时候,往往需要对树结构进行调整,根据维基百科的介绍,删节点主要分为以下几种情况:
1. 删除一个没有孩子的节点:直接删了就行了(孤家寡人,挥一挥衣袖,不带走一片云彩);
2. 删除一个只有一个孩子的节点:删了之后用孩子取代其位置就行了(有点儿像继承家产);
3. 删除一个有两个孩子的节点:比较麻烦。
对于第三种情况,如果称被删除的节点为D,可以选择其中序遍历的前驱E(左子树的最右节点),或者中序遍历的后继E(右子树的最左节点)来取代其位置。然后让E的孩子来取代E的位置(E一定只有一个孩子,要不然E就不能被称之为子树的最右或最左节点)。
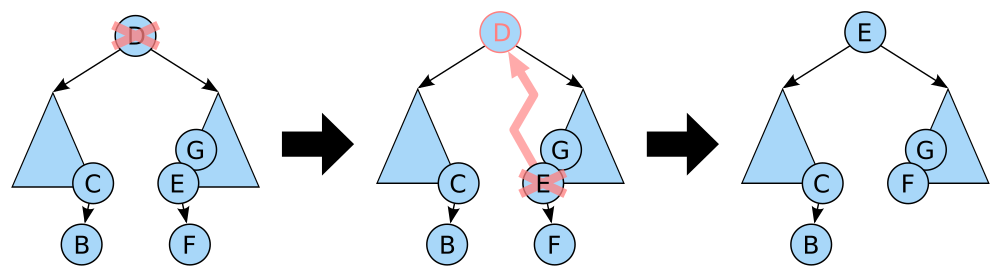
同时要注意的是,不能一直只选择前驱/后继,这样的话相当于是让一棵二叉搜索树往链表的方向发展。所以可以采用轮流的方式。
删除一个节点:首先找到其替代节点,然后删除该节点,并用替代节点替代该节点。
/**
* Remove the node using a replacement
*
* @param nodeToRemoved
* Node<T> to remove from the tree.
* @return nodeRemove
* Node<T> removed from the tree, it can be different
* then the parameter in some cases.
*/
protected Node<T> removeNode(Node<T> nodeToRemoved) {
if (nodeToRemoved != null) {
Node<T> replacementNode = this.getReplacementNode(nodeToRemoved);
replaceNodeWithNode(nodeToRemoved, replacementNode);
}
return nodeToRemoved;
}寻找替代节点:
/**
* Get the proper replacement node according to the binary search tree
* algorithm from the tree.
*
* @param nodeToRemoved
* Node<T> to find a replacement for.
* @return Node<T> which can be used to replace nodeToRemoved. nodeToRemoved
* should NOT be NULL.
*/
protected Node<T> getReplacementNode(Node<T> nodeToRemoved) {
Node<T> replacement = null;
// I. the node has two children
if (nodeToRemoved.greater != null && nodeToRemoved.lesser != null) {
// Two children.
// Add some randomness to deletions, so we don't always use the
// greatest/least on deletion
// always choose the successor or predecessor will lead to an unbalanced tree
if (modifications % 2 != 0) {
replacement = this.getGreatest(nodeToRemoved.lesser);
if (replacement == null)
replacement = nodeToRemoved.lesser;
} else {
replacement = this.getLeast(nodeToRemoved.greater);
if (replacement == null)
replacement = nodeToRemoved.greater;
}
modifications++;
// II. the node has only one child
} else if (nodeToRemoved.lesser != null && nodeToRemoved.greater == null) {
// Using the less subtree
replacement = nodeToRemoved.lesser;
} else if (nodeToRemoved.greater != null && nodeToRemoved.lesser == null) {
// Using the greater subtree (there is no lesser subtree, no refactoring)
replacement = nodeToRemoved.greater;
}
// III. the node has no children
return replacement;
}寻找前驱:
/**
* Get greatest node in sub-tree rooted at startingNode. The search does not
* include startingNode in it's results.
*
* @param startingNode
* Root of tree to search.
* @return Node<T> which represents the greatest node in the startingNode
* sub-tree or NULL if startingNode has no greater children.
*/
protected Node<T> getGreatest(Node<T> startingNode) {
if (startingNode == null)
return null;
Node<T> greater = startingNode.greater;
while (greater != null && greater.id != null) {
Node<T> node = greater.greater;
if (node != null && node.id != null)
greater = node;
else
break;
}
return greater;
}寻找后继:
/**
* Get least node in sub-tree rooted at startingNode. The search does not
* include startingNode in it's results.
*
* @param startingNode
* Root of tree to search.
* @return Node<T> which represents the least node in the startingNode
* sub-tree or NULL if startingNode has no lesser children.
*/
protected Node<T> getLeast(Node<T> startingNode) {
if (startingNode == null)
return null;
Node<T> lesser = startingNode.lesser;
while (lesser != null && lesser.id != null) {
Node<T> node = lesser.lesser;
if (node != null && node.id != null)
lesser = node;
else
break;
}
return lesser;
}删除节点,并用替代节点取代其位置:
/**
* Replace a with b in the tree.
*
* @param a
* Node<T> to remove replace in the tree. a should
* NOT be NULL.
* @param b
* Node<T> to replace a in the tree. b
* can be NULL.
*/
protected void replaceNodeWithNode(Node<T> a, Node<T> b) {
if (b != null) {
// Save for later
Node<T> bLesser = b.lesser;
Node<T> bGreater = b.greater;
// I.
// b regards a's children as his children
// a's children regard b as their parent
// (but a still regards his children as his children)
// Replace b's branches with a's branches
Node<T> aLesser = a.lesser;
if (aLesser != null && aLesser != b) {
b.lesser = aLesser;
aLesser.parent = b;
}
Node<T> aGreater = a.greater;
if (aGreater != null && aGreater != b) {
b.greater = aGreater;
aGreater.parent = b;
}
// II.
// b's children and b's parent know about each other
// (and b has no longer relation with them )
// Remove link from b's parent to b
Node<T> bParent = b.parent;
if (bParent != null && bParent != a) {
Node<T> bParentLesser = bParent.lesser;
Node<T> bParentGreater = bParent.greater;
// b is left child, then it at most has a right child(or its left child'll be the replacementNode)
if (bParentLesser != null && bParentLesser == b) {
bParent.lesser = bGreater;
if (bGreater != null)
bGreater.parent = bParent;
// b is right child, then it at most has a left child
} else if (bParentGreater != null && bParentGreater == b) {
bParent.greater = bLesser;
if (bLesser != null)
bLesser.parent = bParent;
}
}
}
// III.
// b regards a's parent as his parent
// a's parent regards b as his child(but the parent should know about b is it's lesser or greater child)
// (but a still regards his parent as his parent)
// Update the link in the tree from a to b
Node<T> parent = a.parent;
if (parent == null) {
// Replacing the root node
root = b;
if (root != null)
root.parent = null;
} else if (parent.lesser != null && (parent.lesser.id.compareTo(a.id) == 0)) {
parent.lesser = b;
if (b != null)
b.parent = parent;
} else if (parent.greater != null && (parent.greater.id.compareTo(a.id) == 0)) {
parent.greater = b;
if (b != null)
b.parent = parent;
}
size--;
// FINALLY.
// node a should be released
a = null;
}总结
以上就是二叉搜索树的大致用法,但是实际情况中,二叉搜索树用的并非很广泛,因为很难保证数据的来源是绝对无序的。所以构造出来的树自然就是非平衡的。因此AVL的使用才是大势所趋。
参阅
对以下内容作者深表感谢:
1. https://en.wikipedia.org/wiki/Binary_search_tree
2. https://github.com/puppylpg/java-algorithms-implementation/blob/master/src/com/jwetherell/algorithms/data_structures/BinarySearchTree.java