笔记(总结)-PCA(主成分分析)

主成分分析是一种特征抽取手段，通过将样本从原始空间映射到低维空间实现特征数量的减少，而低维空间中某一维度实际上是原始空间的一种“杂糅”表示。在之前的博客中提到过参考链接，由于PCA涉及的数学手段包括矩阵、特征值和特征向量，参考笔记-矩阵与特征值这一篇，对其有一定理解后再来看PCA算法就比较清晰了。

首先给出PCA算法：

对所有样本进行中心化： $x_i \leftarrow x_i- \frac{1}{m} \sum_{i=1}^{m}x_i$
计算样本的协方差矩阵 $X X^T$
对协方差矩阵 $X X^T$ 做特征值分解
取最大的k个特征值所对应的特征向量 $w_1,w_2,...,w_k$

得到投影矩阵 $w=(w_1,w_2,...,w_k)$ 。

首先跳过step1先看step2，看看为什么需要计算样本的协方差矩阵。给出协方差(covariance)定义如下：

c o v (X, Y) = E [(X - E (X)) (Y - E (Y))]

$cov(X,Y)=E[(X-E(X))(Y-E(Y))]$

是两个变量偏离各自均值的乘积的期望。当两个变量变化趋势相同时，即当 $X$ 大（小）于 $E(X)$ 时， $Y$ 也大（小）于 $E(Y)$ ，协方差取较大正值；若两个变量变化趋势相异甚至相反时，协方差取较大负值。因此协方差可以衡量两个变量变化趋势的相似性，即变量相关性。

对于 $n$ 维随机变量 $x=(x_1,x_2,...,x_n)^T$ ，称矩阵：

C = (c_{i j})_{n \times n} = [\begin{matrix} c_{11} & c_{12} & \dots & c_{1 n} \\ c_{21} & c_{22} & \dots & c_{2 n} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ c_{n 1} & c_{n 2} & \dots & c_{n n} \end{matrix}]

$C=(c_{ij})_{n\times n}= \begin{bmatrix} c_{11} & c_{12} & \cdots & c_{1n} \\ c_{21} & c_{22} & \cdots & c_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ c_{n1} & c_{n2} & \cdots & c_{nn} \\ \end{bmatrix}$

为 $n$ 维变量 $x$ 的协方差矩阵，其中：

c_{i j} = c o v (x_{i}, x_{j})

$c_{ij}=cov(x_i,x_j)$

对于给定的样本矩阵 $X=(x_{ij})_{n \times m}(m$ 个 $n$ 维变量)，参考关于协方差矩阵的理解最终得到协方差矩阵为：

C = \frac{1}{m} X X^{T}

$C=\frac{1}{m}XX^T$

此时回到step1，可以看到只是少了 $\frac{1}{m}$ ，而这只是一个尺度伸缩，对PCA算法并无影响。因此在算法最初对样本进行均值化，是为了让算法后面的计算有意义，而不是某种预处理，实是属于算法的一部分。

那为什么需要用协方差矩阵呢？这就涉及到PCA算法的目的：将样本从原始空间映射到低维空间实现特征数量的减少。这种映射可以用下图形象表达：
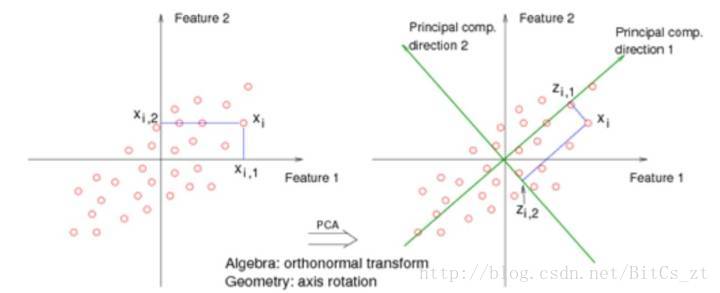
这里写图片描述
绿色的轴对应了某种投影（即映射）方向，显然在direction 1 方向上样本方差是很大的，比较容易能将其区分开来。我们希望投影后能最大程度地区分样本，这可以等价为“最大化投影后的方差”，此时有：

可以看到当我们在单位正交基的限制条件下 $||w||=1$ ，最大投影后的方差，用拉格朗日乘数法求解，得到等价的最大化目标为 $\max w^TTSw=w^T \lambda w=\lambda$ ，即最大化矩阵 $S$ (即上文中的样本矩阵 $X$ )的特征值，投影向量即为特征值对应的特征向量。

再换一个角度思考，将样本投影之后，我们希望减少某些维度，从而获取对样本的“更简洁”的表示。而减少维度的准则是：在减小维度之后，能最大程度地还原回到减小之前。好比我们找到了一个新的视角来看这个问题，但是在新视角上我们希望看问题看得更简单，因为这种“简单”我们可能会忽略一些东西，而被忽略的东西对解决问题并不重要。这样即得到了“最小化重建后的误差”。此时有：
这里写图片描述

假如样本原始空间和投影空间的维数为 $D$ ，我们要在投影之后减少1个维度，计算重建误差如下：
这里写图片描述
最终误差等于即为 $u_D^TSu_D$ （被去除的是第D个维度），而由上最大化方差的推导结果，这恰好等于特征值 $\lambda_D$ 。也就是说，最小化重建误差等价于最小化被去除维度对应的特征值，这和最大化投影方差的结果是等价的。

此时可以解释PCA算法的step3、step4。对协方差矩阵做特征分解，得到与原始空间维度相同的投影空间，每个特征值 $\lambda$ 对应的特征向量为某个投影方向。我们保留较大的 $\lambda$ 对应的特征向量，使得投影后方差大，样本更能区分开；去除较小的 $\lambda$ 对应的特征向量，使得投影后重建误差小。 $\lambda$ 对应的特征向量即为投影向量。

回到所举示例进行说明：
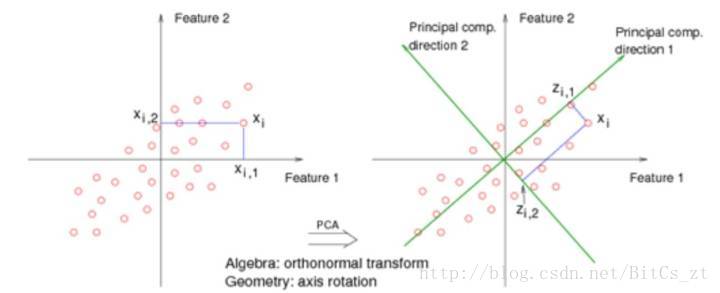
这里写图片描述
原始空间和投影空间都为2维，显然direction 1上样本方差更大，而direction 2上样本方差很小，不易区分。去除direction 2对应的维度，投影空间变为1维，样本将落于direction 1对应的直线上。

PCA算法解释完毕。我们首先跳过step1来分析step2，解释了协方差和协方差矩阵，协方差矩阵的推导自然就解释了step1。而后从“最大化投影方差”和“最小化重建误差”，解释了为什么需要对协方差矩阵进行矩阵分解，并选取较大特征值对应的特征向量作为投影向量。以上主要是公式推导，如果参阅了本文最开始提供链接中关于矩阵概念的分析，对PCA的算法原理会理解得更加透彻。简要描述我从该链接中总结的东西：

矩阵是一种变换（对原始空间旋转和缩放的融合）
矩阵的特征向量对应的是该变换的缩放方向（可理解为旋转过后的坐标轴方向）
矩阵的特征值对应的是不同缩放方向的缩放程度

若将原空间中样本比作某物体运动下轨迹图，则PCA相当于找到了物体运动最剧烈的方向。由于协方差矩阵中的元素是各个维度随机变量的协方差（即样本空间中各样本特征之间的相关性），我们做的实际上是找出了缩放程度最大、最能描述样本特征相关性的若干个方向。

虽然PCA算法使用场景有限，但是其背后的思想内涵是很丰富的。十分值得学习理解。

参考链接如下：
如何理解矩阵特征值？ - 知乎
 主成分分析PCA算法：为什么去均值以后的高维矩阵乘以其协方差矩阵的特征向量矩阵就是“投影”？ - 知乎
 关于协方差矩阵的理解 - CSDN博客
周志华西瓜书

笔记(总结)-PCA(主成分分析)

猜你喜欢