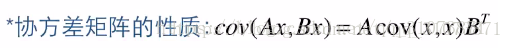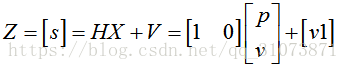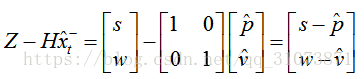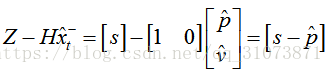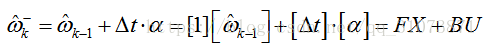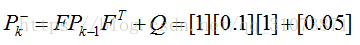一般我们编程中,常用的数学模型都是离散的,首先看一下离散的状态空间表达式:
上面这张表格来自百度百科“状态空间”
下面看一个实际问题:《卡尔曼滤波器的原理以及在matlab中的实现》
https://www.bilibili.com/video/av10788247?from=search&seid=10382691491488446111
问题描述:一辆小车,我们可以任意控制它的加速度u(t),要求实时输出它的路程p(t)。
上面图中推导出的公式,就是卡尔曼状态预测公式,式中的F矩阵称为状态转移矩阵,B矩阵叫做控制矩阵。另外,①变量上面戴帽子,指的是该变量是个预测值,不是真实值,②左侧的x帽右上角还带减号,减号的意义是,这个x帽还不是最终的预测值,待会我们还要继续修正他。
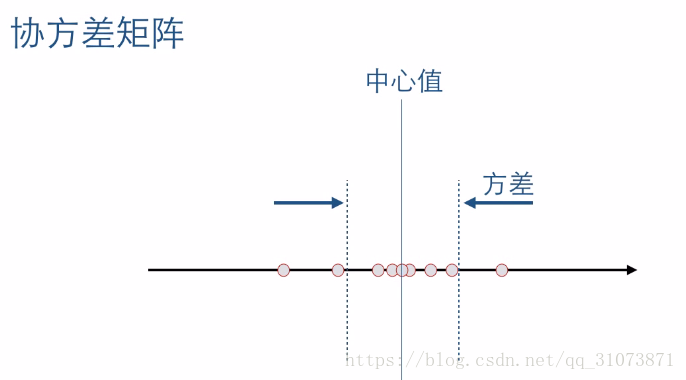
下面再来看一下协方差矩阵的直观解释,我们从一维数据开始逐步理解他:
上图中的圆点为一些样本数据,它们是带有高斯噪声的,于是这些样本就表现为:围绕在中心值附近,离散程度用方差来表示。换句话说,一维数据的协方差就是方差。那么二维数据的协方差从直观上怎么理解呢?看下图:
一组二维样本,例如(2,1)、(2.3, 4)、(3, 4.5)·····,如何描述这组样本的分布情况呢?一个直观的想法是,向上图中的图1一样,把这组二维样本分别投影到X/Y轴,这样就得到了两组一维的样本,这样每一组样本都能获得中心值和方差两个参数了,但是这种思路只能描述二维数据的两个维度相互独立的情况,如果说,这两个维度的数据不是相互独立的(例如,当第一维的数据的噪声为正值时,第二维的数据的噪声也大概率为正值),这种情况下我们就不能用两个一维的方差来描述二维样本的分布情况了,而必须把两者的相关性也考虑进来。下面再看一下协方差矩阵的数学定义:
仔细观察上述定义式,可知:如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值时另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值;如果两个变量的变化趋势相反,即其中一个变量大于自身的期望值时另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。
我们还发现,Cov(X,X)的公式其实就是单变量方差的公式:
对于两个随机变量X、Y的协方差矩阵就有4个元素:Cov(X,X)、Cov(X,Y)、Cov(Y,Y)、Cov(Y,X),
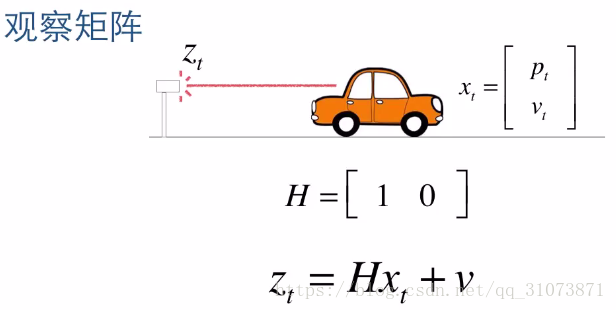
上图中,H称为观测矩阵(其实就是状态空间表达式中的“输出矩阵C”),z为测量值(例如,激光测距的值),v为测量误差。如果我们能从小车外部测量到多个参数,例如我们能测到小车的路程s和实时速度w,那么测量值Z就不再是一个标量值了,而变为一个列向量:
如果只能测到路程s,那么上式就简化为:
由此可见,观测矩阵(输出矩阵)的物理意义就是:根据状态向量的值(这个值可能是测量值,也可能是数学模型算出的先验估计值),输出我们想要的变量的值。
前文中,我们提到,预测模型给出的预测值,并不是一个最优值,我们需要对它进行修正,修正方法如下:
上式中,

这个差值也有可能是个矩阵,这跟测量值的个数有关,如果测量值Z是列向量,那么,该差值展开后即为:
如果只能测量距离s,那么上式就退化为:
上面几个式子中,
P为状态协方差矩阵,其意义是,我们的先验估计
Q为状态转移协方差矩阵,其意义是,矩阵F到底有多大的“不可信度”;
H为观测矩阵,其功能是把几个状态变量线性叠加为输出变量,矩阵的值就是叠加所用的系数;
F为状态转移矩阵;
R为观测噪声的协方差矩阵,其意义是,我们的测量值到底有多大的“不可信度”;
P矩阵的初始值根据经验/历史样本随便设置一个差不多的值即可,别太夸张就行,该矩阵会自己迭代为合适的值,例如我们设置的P过大(倾向于不相信预测模型),结果在迭代中发现,预测的值还是挺准的,那么第5式就会自动把P给减小(倾向于相信预测模型)
卡尔曼增益K的物理意义,其实很简单,就一句话:你是更相信测量值,还是更相信先验估计值,这个K就代表了你对测量值的信任程度。对测量值和先验估计值的信任程度的比例K是如何求的?那就是第3式的工作了,第3式根据测量值的误差协方差R和先验估计值的协方差P-的大小,来决定K的大小,显然,测量值的误差协方差R越小,计算出的K值越大。
定量的来看一下极端情况,假设我们完全相信先验估计,也即R=0矩阵,那么K的计算结果就是
关于状态转移协方差矩阵Q,我们这样来理解它:状态向量X有两个元素,路程p和速度v,我们用数学模型预测递推求解新的状态向量时,是这样求解的:


下面我们把卡尔曼滤波用在“角度传感器和角加速度传感器,获取真实角度”这个问题中,问题描述:在一个物体上安装了一个角度传感器和一个角加速度传感器,角度传感器的特性是物体动作较慢时,测量很准确,但物体动作较快时,读取出的测量结果带有很大的噪声,但均值基本是对的,而角加速度传感器,在物体动作很快时,仍可以准确的测量出角加速度,但是因为控制器只能以一定的时间间隔周期性的读取角加速度,所以,无法求角加速度的积分,也就无法用角加速度的积分来求角度了,只能用Σ(αxΔt)来近似代替积分从而计算出角度,显然这种近似会随着时间的推移,累计误差越来越大。实际上这个问题用互补滤波就可以简单粗暴的解决,但这里为了学习卡尔曼,我们用卡尔曼滤波来解决下这个问题。
先定义几个变量:角速度为ω,角加速度为α,角度为a,所有变量的预测值都用帽子表示,
按照卡尔曼的标准五步来做:
(1)建立角度的预测模型(这是一个:非时变的离散的状态空间模型)
F为状态转移矩阵,B为控制矩阵,X为状态,U为输入向量,因为这个问题比较简单,所以很多矩阵都退化成了1x1的标量。
该式计算出的结果,被称为“先验估计”,其右上角带个减号,所谓先验和减号,其物理意义就是,待会还要修正这个估计的值。
(2)写出对预测模型的不确定度,也即状态协方差矩阵P
上式中,F为状态转移矩阵,Pk-1为上一运算周期修正过的状态协方差矩阵(若本次计算为首次计算,那么Pk-1就是状态协方差矩阵的初值),Q为状态转移协方差矩阵,我们对预测模型的不确定度进行了定量计算,显然它由两部分组成:①数学模型中
在那个英文的卡尔曼视频中讲到,对于状态向量只含一个元素的系统,P矩阵其实就是“先验估计