主成分分析（PCA）原理与实现

主成分分析（PCA）是最重要的数据降维的方法之一。针对高维数据的处理时，往往会因为数据的高维度产生大量的计算消耗，为了提高效率，一般最先想到的方法就是对数据降维。与“属性子集选择”的方法（即选择一部分有代表意义的属性直接替代原数据）不同，PCA是通过创建一个由原数据中的属性“组合”而成的，数量较小的变量集合来替代原数据。

PCA的基本思想可以这样描述：找出数据的所有属性中最主要的部分，用这个部分替代原始数据，从而达到降维的目的。显然，降维后的数据肯定会有所损失，而我们的目的，是要尽可能地保留原始数据的特征。所以，PCA的核心在于如何寻找这个“最主要部分”。

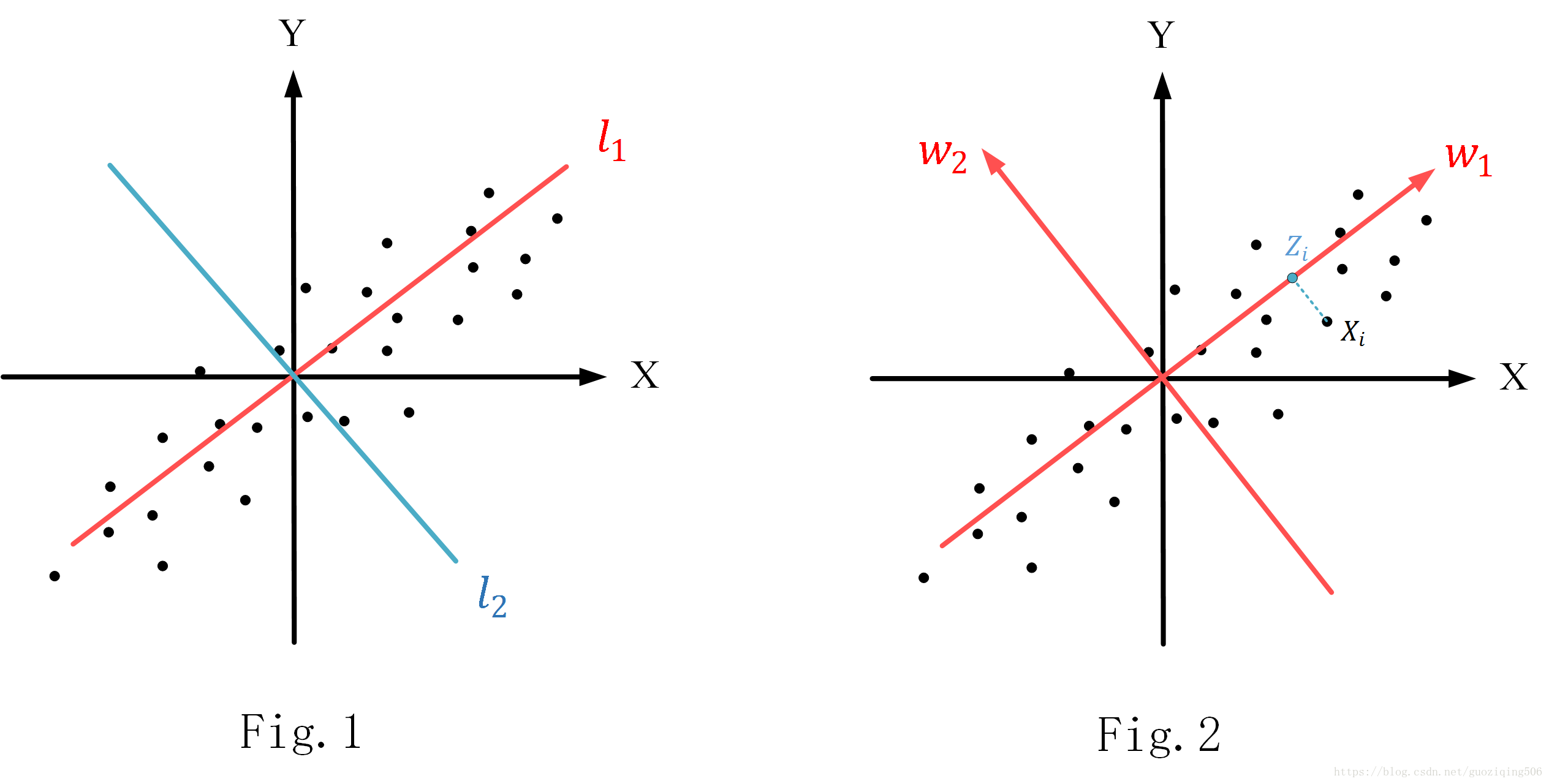
比如，现在有一组二维数据集合，如图Fig.1所示，如果要对这些二维数据降维到一维，那很容易想到在这个坐标系中找到一条直线，然后将所有的二维数据点都映射到这条直线上，我们再处理这些映射后的点，就相当于是直接对一维数据做处理了。但是找这样一条线是很讲究的，比如Fig.1中，X轴，Y轴，还有我标出的 $l_1, l_2$ 四条线，你说映射到哪条线更好呢？显然是 $l_1$ ，因为样本点的投影在这条直线上能够尽可能地分开，你可以理解为最大限度的保留了数据特征（反过来想，如果投影后，尽可能地分不开，那数据点不都一样了，还有啥特征、区分啊）。

PCA要解决的，就是如何找这样一条直线。当然，如果我们想要将 $n$ 为空间的数据降到 $k$ 维（ $n > k > 0$ ）空间上去，那实际上找的是一个 $k$ 维的超平面。其实，根据Fig.1我们不难发现：如果数据点集是完全无规律的随机分布，那么PCA的效果不会太好（因为不管找怎样一个超平面都会损失大量特征）；而如果数据的维度之间存在相关关系，比如某个属性与另外一个属性或者属性的组合成一定的比例关系（像Fig.1中，X与Y就基本成正比例关系），则使用PCA时非常合适的。

刚才说了，找超平面的理论依据是“在超平面上的投影点要尽可能地分开”，那换句话说，就是要找到超平面，使之具备最大的“投影方差”。下面做一个详细的推导。

PCA原理推导：基于最大投影方差

对于 $m$ 个 $n$ 维数据向量 $\{X_1, X_2, \dots, X_m\}$ ，我们默认他们都已经经过了“中心化”处理，即 $\sum_{i = 1}^{m}X_i = 0$ ，如Fig.2所示。

(1) 假设现在找到了最佳的超平面（维度是 $k$ ），那我们旋转现有的坐标系，使其中的 $k$ 个坐标轴组成的超平面就是我们要投影的超平面。这个过程相当于做基变换，变换过程中，我们令变换后的基是一组标准正交基，记为 $W = \{w_1, w_2, \dots, w_n\}$ （ $W$ 正是标准正交基）

(2) 基变换完成之后，不难得到新的坐标系下，原先数据的坐标。以 $X_i$ 来说，记新的坐标为 $Y_i$ ，则 $Y_i$ 可如下计算得到：

\begin{matrix} (1) & (\begin{matrix} Y_{i 1} \\ Y_{i 2} \\ ⋮ \\ Y_{i n} \end{matrix}) = {(\begin{array}{cccc} w_{11} & w_{12} & \dots & w_{1 n} \\ w_{21} & w_{22} & \dots & w_{2 n} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ w_{n 1} & w_{n 2} & \dots & w_{n n} \end{array})}^{- 1} (\begin{matrix} X_{i 1} \\ X_{i 2} \\ ⋮ \\ X_{i n} \end{matrix}) = W^{T} X_{i} \end{matrix}

$\begin{equation} \left( \begin{array}{c} Y_{i1}\\ Y_{i2}\\ \vdots\\ Y_{in}\\ \end{array} \right) = \left( \begin{array}{cccc} w_{11} & w_{12} & \dots & w_{1n} \\ w_{21} & w_{22} & \dots & w_{2n} \\ \vdots & \vdots & \ddots& \vdots \\ w_{n1} & w_{n2} & \dots & w_{nn} \\ \end{array} \right)^{-1} \left( \begin{array}{c} X_{i1}\\ X_{i2}\\ \vdots\\ X_{in}\\ \end{array} \right) = W^TX_i \end{equation}$

(3) 因为要将 $n$ 维的数据降维到 $k$ 维，那我们需要在新的坐标系下，舍弃一些维度。记舍弃了这些维度之后的坐标系为 $W' = \{w^{(1)}, w^{(2)}, \dots, w^{(k)}\}$ ，其中 $w^{(j)}$ 表示在低维空间中的第 $j$ 个基向量。现在，我们可以得到投影点在坐标系 $W'$ 中的坐标（记为 $Z_i$ ）：

\begin{matrix} (2) & Z_{i} = (Y_{i}^{(1)}, Y_{i}^{(2)}, \dots, Y_{i}^{(k)}) = W^{' T} X_{i} \end{matrix}

$\begin{equation} Z_i = (Y_i^{(1)}, Y_i^{(2)}, \dots, Y_i^{(k)}) = W'^TX_i \end{equation}$
实际上，上式中的

Z_{i}

$Z_i$ 就是直接把

Y_{i}

$Y_i$ 舍弃了一部分坐标得到的。

(4) 对于任意的数据向量 $X_i$ ，它在降维后的坐标系中的坐标为 $Z_i$ ，而 $Z_i$ 的方差由公式 $Z_iZ_i^T$ 得到，即：

\begin{matrix} (3) & V a r (Z_{i}) = W^{' T} X_{i} X_{i}^{T} W^{'} \end{matrix}

$\begin{equation} Var(Z_i) = W'^TX_iX_i^TW' \end{equation}$

因为一共有 $m$ 个点，所以我们把它们加和求最大：

\begin{matrix} (4) & \sum_{i = 1}^{m} V a r (Z_{i}) = t r (W^{' T} X X^{T} W^{'}) \end{matrix}

$\begin{equation} \sum_{i = 1}^m Var(Z_i) = tr(W'^TXX^TW') \end{equation}$

这个计算过程的详细推导可以参考博文：主成分分析（PCA）原理总结。我的这篇博客的主要内容也是参考了这篇文章，如果对我写的有疑问，可以参考一下。

(5) 至此，得到优化问题：

\begin{matrix} (5) & max t r (W^{' T} X X^{T} W^{'}) s . t . W^{' T} W = E \end{matrix}

$\begin{equation} \max tr(W'^TXX^TW') ~~~~~~s.t. W'^TW = E \end{equation}$
其中，

E

$E$ 为单位矩阵.

这个问题很容易求解，我们直接观察就能知道当 $W'$ 取其 $k$ 个特征值最大的特征向量时， $tr(W'^TXX^TW')$ 最大。

我大概说说我对于求解这个优化问题的理解： $XX^T$ 是数据集的协方差矩阵（那也就是固定的），而 $W'$ 的每个向量都是标准正交基；因此， $tr(W'^TXX^TW')$ 的取值应该是矩阵 $XX^T$ 的最大的 $k$ 个特征值的和。那自然就知道，我们需要 $W'$ 就是由这 $k$ 个最大特征值所对应的特征向量构成的。

以上即为PCA的原理，下面我们根据上述原理，总结一下PCA的具体步骤。

PCA实现步骤

预处理：对所有的数据进行中心化处理， $X_i = X_i - \frac{1}{m} \sum_{i = 1}^m X_i$ ；
计算样本的协方差矩阵 $XX^T$ ，得到一个 $n \times n$ 的矩阵；
计算 $XX^T$ 的特征值及特征向量，取特征值最大的 $k$ 个特征向量做标准化处理，再作为列向量构成 $W'$ ( $n \times k$ 矩阵)；
对于每个数据 $X_i$ ，计算它在新坐标系 $W'$ 中的坐标 $Z_i = W'^TX_i$ （ $Z_i$ 为 $k$ 维向量）

写到这里，你再看看整个这4步，是不是感觉有点眼熟？和我在之前的博客: 奇异值分解中说的过程可以说几乎一模一样。只不过这里不需要考虑奇异值分解中的左矩阵 $U$ ，而直接使用右矩阵 $V$ 就行了。其实，本质上PCA就是通过奇异值分解来实现降维的。

那反过来讲，在事先不知道参数 $k$ 的情况下，我们也能先做奇异值分解，再把分解后对角矩阵对角线上较小的 $k$ 个元素（即较小的 $k$ 个奇异值）直接变为0，而将数据降维。

总结

最后，总结一下PCA的优缺点：

优点：

仅仅需要以方差衡量信息量，不受数据集以外的因素影响；
各主成分之间正交，可消除原始数据成分间的相互影响的因素；
计算方法简单，易实现；

缺点：

主成分各个维度的含义模糊，不易于解释；
方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响