并查集（Union-Find Set）

并查集的三种操作

（1）Union(Root1, Root2):把子集合Root2并入集合Root1中。要求这两个集合互不相交，否则不执行合并。
（2）Find(x)：搜索单元素x所在的集合，并返回该集合的名字。
（3）UnionFindSets(s):构造函数，将并查集中s个元素初始化为s个只有一个单元素的子集合。 --------------------- 本文来自 razor_edge 的CSDN 博客，全文地址请点击：https://blog.csdn.net/weixin_37818081/article/details/78633187?utm_source=copy

我们可以把每个连通的分量看成一个集合，该集合包含了连通分量中的所有点。这些点两两连通，而具体的连通方式无关紧要，就好比集合中的元素没有先后顺序之分，只有属于和不属于的区别。在图中，每个点恰好属于一个连通分量，对应到集合表示中，每个元素恰好属于一个集合。换句话说，图的所有连通分量可以用若干不相交集合来表示。

并查集的精妙之处在于用树来表示集合。例如，若包含点1,2,3,4,5,6的图有3个连通分量{1,3}，{2,5,6},{4}，则需要用三棵树来表示。这三棵树的具体形态无关紧要，只要有一棵树包含1,3两个点，一棵树包含2,5，6这三个点，还有一棵树只包含4这一个点即可。我们规定每棵树的根节点是这棵树所对应的集合的代表元（representative）。

如果把x的父节点保存在p[x]中（如果x没有父亲，则p[x]等于x），则不难写出“查找节点x所在数的根节点”的递归程序：

int find(int x){p[x]==x?x:find(p[x]);}

翻译成大白话就是：如果p[x]等于x，说明x本身就是树根，因此返回x；否则返回x的父亲p[x]所在树的树根。

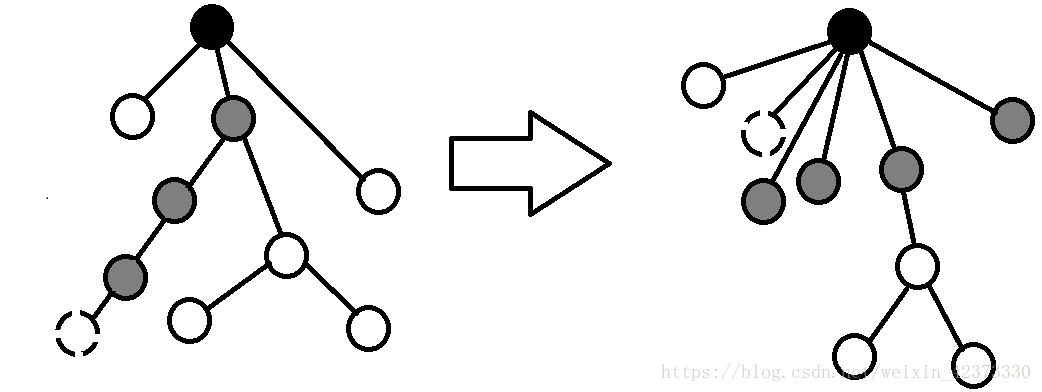
问题来了：在特殊情况下，这棵树可能是一条长长的链。设链的最后一个结点为x，则每次执行find(x)都会遍历整条链，效率十分低下。看上去是个棘手的问题，其实改进方法很简单。既然每棵树表示的只是一个集合，因此树的形态不变，只要顺便把遍历过的结点都改成树根的儿子，下次查找就会快很多了，如图所示：

这样，Kruskal算法的完整代码便不难给出了。假设第i条边的两个端点序号和权值分别保存在u[i],v[i]和w[i]中，而排序后第i小的边的序号保存在r[i]中（顺便说一句，这叫做间接排序——排序的关键字是对象的“代号”，而不是对象本身）。

int cmp(const int i, const int j) {return w[i]<w[j]; } //间接排序函数
int find(int x ){ return p[x]==x?x:p[x]=find(p[x]); }//并查集的find
int Kruskal()
{
    int ans=0;
    for(int i=0;i<n;i++) p[i]=i; //初始化并查集
    for(int i=0;i<m;i++) r[i]=i; //初始化边序号
    sort(r,r+m,cmp); //给边排序
    for(int i=0;i<m;i++)
    {
        int e=r[i]; int x=find(u[e]); int y=find(v[e]); //找出当前边两个端点所在集合的编号
        if(x!=y) {ans+=w[e];p[x]=y;} //如果在不同集合，合并 -----问题①
    }
    return ans;
}

注意问题①部分不能写成p[u[e]]=p[v[e]],因为u[e]和v[e]不一定是树根（执行的find之后，才行）

并查集（Union-Find Set）

猜你喜欢