DAG图与AOV网
一个无环的有向图称为有向无环图(DAG)。图的顶点可以表示要执行的任务,并且边可以表示一个任务必须在另一个之前执行的约束; 在这个应用程序中,拓扑排序只是任务的有效序列。 当且仅当图形没有有向循环时,即如果它是有向无环图(DAG),则可以进行拓扑排序。 任何DAG都具有至少一个拓扑排序。这种用弧来表示活动之间的优先级关系的有向图,称为顶点表示的活动的网(简称AOV网)。
拓扑排序(Topological sorting)
在计算机科学领域,有向图的拓扑排序或拓扑排序是其顶点的线性排序。在图中假设从顶点 i 到顶点 j 中有一条有向路径 i -> j。那么我们称 i 为 j 的前驱,称 j 为 i 的后继。
拓扑排序的算法非常简单,常用的方式为Kahn’s algorithm算法。基本步骤为:
- 在给定的有向图中,选择其中一个没有前驱的顶点放入容器中
- 从图中删除该顶点及其所有的以其为尾的弧。
- 重复上述两步,直至全部顶点输出或者不存在没有前驱的顶点为止。
该算法的伪代码如下:
L ← 用来存放输出的节点的列表
S ← 没有前驱的所有点的集合
while S is non-empty do //当S不为空时
remove a node n from S //从集合S中移除节点N,
add n to tail of L //并将节点N放在列表的尾部
//循环遍历每一个从节点N到节点M的边e
for each node m with an edge e from n to m do
//j将该边从图中移除
remove edge e from the graph
//如果移除后节点m没有以它为入度的边,便将m插入到集合S中
if m has no other incoming edges then
insert m into S
//否则,图中必定含有其他方向的边
if graph has edges then
//于是返回错误,表明此时图中至少含有一个环
return error (graph has at least one cycle)
else
return L (a topologically sorted order)
下面用一个实例来说明一下拓扑排序的整个流程;
-
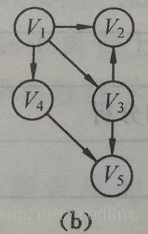
假定给我们一个有向图如下图所示:
找出它的拓扑排序。那么我们可以这样来。 -
先找没有直接前驱的节点,在这里V1,v6都没有直接前驱,那么任意选择一个,并删除所有以其为尾的弧。(假定我们选择的是v6),那么此时L的列表中的元素为 L = {v6}
-
重复上述步骤我们可以移除V1,得到L = {v6,v1}.
-
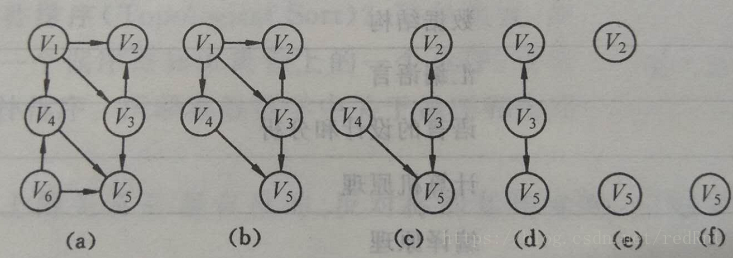
反复如此,直到所有的顶点都输出完毕或者不存在没有前驱的顶点为止。整个流程如下:
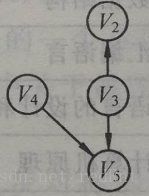
由此我们可以看出拓扑排序的顺序并不是唯一的。对于下面这幅图就可以有多种拓扑顺序:
利用DFS实现拓扑排序
当一个有向图无环的时候,我们可以利用DFS算法来实现拓扑排序。原理很简单,由于图中没有环,那么由图中某点出发的时候,最先退出DFS的顶点一定是出度为0的顶点,也就是拓扑排序中最后的一个顶点(逆向思维)。因此按DFS退出的先后记录下的顶点序列就是逆向的拓扑排序的序列。
具体的分析就不来了,伪代码贴上:
L ← Empty list that will contain the sorted nodes
while there are unmarked nodes do
select an unmarked node n
visit(n)
//定义这样的visit函数
function visit(node n)
if n has a permanent mark then return
if n has a temporary mark then stop (not a DAG)
mark n temporarily
for each node m with an edge from n to m do
visit(m)
mark n permanently
add n to head of L
拓扑排序的应用
拓扑排序最常见的应用是基于其依赖性来调度一系列作业或任务。作业由顶点表示,如果在作业y开始之前必须完成作业x,那么就存在从x到y的边(例如,洗衣服时,洗衣机必须在我们将衣服放入烘干机之前完成) 。然后,拓扑排序给出了执行作业的顺序。 20世纪60年代早期,在PERT技术项目管理调度的背景下,首次研究了拓扑排序算法的密切相关应用(Jarnagin 1960);在此应用程序中,图形的顶点表示项目的里程碑,边表示必须在一个里程碑与另一个里程碑之间执行的任务。拓扑排序构成了线性时间算法的基础,用于查找项目的关键路径,一系列里程碑和任务,用于控制整个项目进度的长度。
而对于上面4中的第二种情况我们可以知道,这个时候图中的所有节点肯定是没能全部输出来的,因此我们可以得到一个判断AOV网中是否存在环的判定方法:对于有向图构造其顶点的拓扑序列,若网中的所有顶点都在该拓扑序列中,那么该AOV网就不存在环。反之有环。这个结论学过计算机操作系统的人来说并不陌生。一个作业必须在另外一个作业完成之后才能执行,这在操作系统中对应进程间的同步关系。而我们常用前驱图来表示其关系。而在进程间的关系中往往存在死锁。而检测死锁的方法,就是拓扑排序法。(更多详细内容去学习《操作系统》课程吧)