【填坑】DP·斜率优化&【hdu】3507

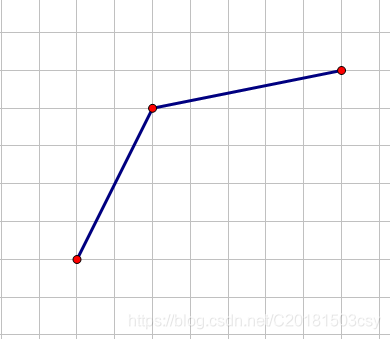
我们先给一个例子：
【hdu3507】给定n个正数与M（n∈[1,500000]），将它们分成若干段输出。输出一段的费用按下法计算：
$cost=(\sum_{i=1}^{k}a_i)^2+M$
求最小的 $cost$ 。
如果n小一些，这个题就应该属于DP入门题的那一类了吧：
令 $f[i]$ 为输出前 $i$ 段的最小费用，则有：
$f[i]=min\{f[j]+w(j+1,i)^2+M|1≤j<i\},w(i,j)\sum_{k=i}^{j}a_k$
时间复杂度为 $O(n^2)$ ，绝壁TLE！
~~自闭ing…TAT~~
~~自闭够了，接着想办法优化~~
观察这个DP式（假设j为一个决策点，即要更新 $f[i]$ 的点）：
$f[i]=f[j]+w(j+1,i)^2+M$
令 $sum[i]$ 为前i项之和，则有：
$f[i]=f[j]+(sum[i]-sum[j])^2+M$
假设还有另一决策点k：
$f[i]=f[k]+(sum[i]-sum[k])^2+M$
它比j更优，则有：
$f[j]+(sum[i]-sum[j])^2+M>f[k]+(sum[i]-sum[k])^2+M$
打开括号，消去相同项：
$f[j]-2sum[i]sum[j]+sum[j]^2>f[k]-2sum[i]sum[k]+sum[k]^2$
整理一下：
$2(sum[k]-sum[j])sum[i]>(sum[k]^2-sum[j]^2)+(f[k]-f[j])$
令 $\Delta x=2(sum[k]-sum[j]),\Delta y=(sum[k]^2+f[k])-(sum[j]^2+f[j])$ 。因为 $a_i$ 都是正数，所以 $sum[i]$ 单增。
若 $k>j$ ，则：
$sum[i]>\frac{\Delta y}{\Delta x}=k_l$
等价于k比j优。
若 $k <j$ ，则：
$sum[i]<\frac{\Delta y}{\Delta x}=k_l$
等价于k比j优。
综上，若编号小的更优，则 $sum[i]<\frac{\Delta y}{\Delta x}=k_l$ ，反之， $sum[i]>\frac{\Delta y}{\Delta x}=k_l$ 。(这个结论很重要，请记一下)
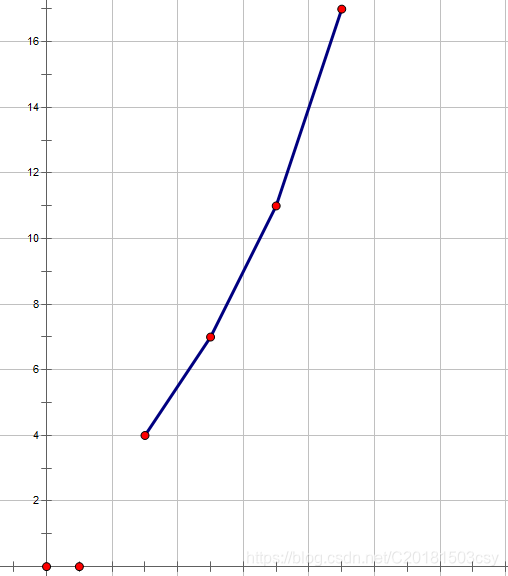
看见这个式子，我们自然地容易与斜率联系在一起（这点很重要！！！并且为了方便大家看出，已对柿子进行改写）。于是，我们把它搬到坐标系上：
在这里插入图片描述
~~由于忘了命名了，~~ 规定由下往上依次为 $i$ , $j$ , $k$ 。
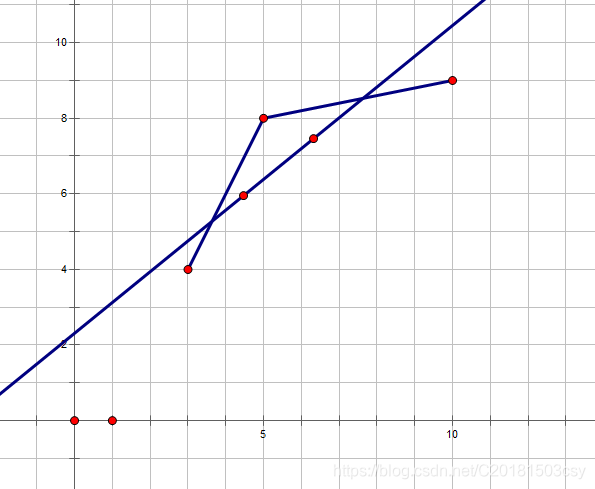
然后我们证明一个东西：若 $k_{ij}>k_{jk}$ ，则 $j$ 一定不是最佳决策点。理由如下：
依旧以上面的问题为例：
若 $sum[i]>k_{ij}$ ：

则 $i$ 比 $j$ 优， $j$ 比 $k$ 优
若 $k_{ij}>sum[i]>k_{jk}$
在这里插入图片描述
则 $i$ 比 $j$ 优， $k$ 比 $j$ 优
若 $k_{ij}>sum[i]>k_{jk}$

则 $k$ 比 $j$ 优， $j$ 比 $i$ 优
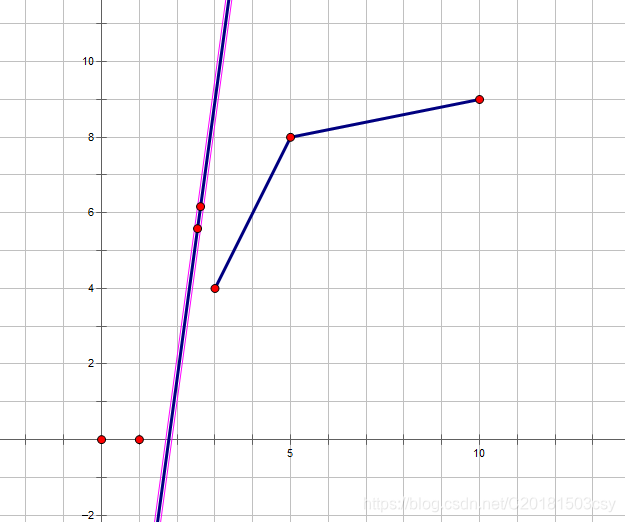
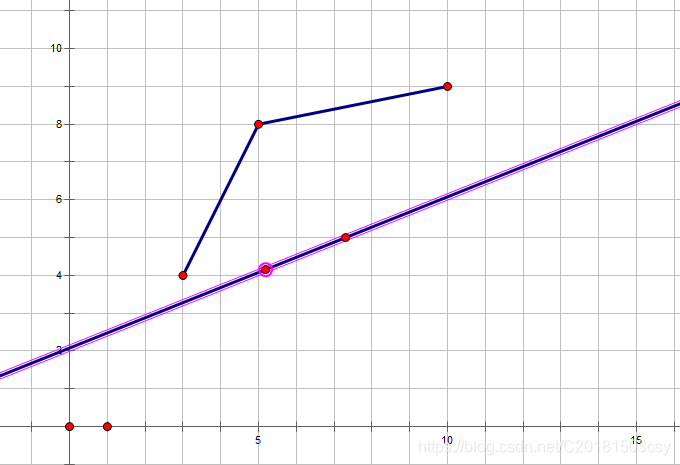
综上，j一定不是最佳决策点。于是，如果将最佳决策点用线连起来，就形成了一个下凸包：

所以 $k_1<k_2<k_3<...<k_i$
单调队列！ $O(n)$ ！
由于 $sum[i]$ 单增，所以我们可以不断地将队头小于 $sum[i]$ 的踢出队列，最后剩下的队头即是最佳决策点。
然而，计算 $k$ 的值需要用除法，于是就要考虑精度的问题。这~~恶心的东西~~显然是我们想回避掉的。于是，我们在这里介绍一些判断下凸包的方法。

【法1】

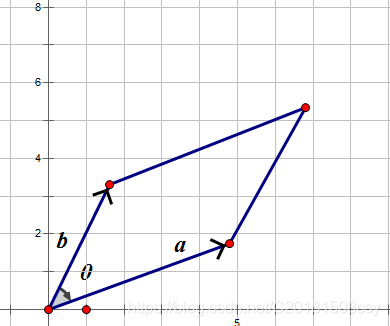
如果我们将 $ij$ 看做 $\vec{a}$ ， $jk$ 看做 $\vec{b}$ 。我们将它们平移到同一点（原点）（ $\theta$ 角不小心画反了，请谅解）：
在这里插入图片描述
在这种情况下，原图形是一个下凸包。由平行四边形的面积公式：
$S=|\vec{a}||\vec{b}|sin\theta$
由于 $sin\theta>0$ ，故面积大于0。
而如果是这样：

在这种情况下，原图形是一个上凸包。由平行四边形的面积公式：
$S=|\vec{a}||\vec{b}|sin\theta$
由于 $sin\theta<0$ ，故面积小于0。
于是，我们可以根据这个方法，就可以判断下凸包了。
但是，由于涉及到三角函数，又得使用浮点数，还是得考虑精度问题。这样一来，上述分析好像就没啥卵用了耶!

两个向量a和b的叉积 $\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|sin\theta=x_1y_2-x_2y_1$

于是我们成功避开了精度问题。
（P.S.:由上述分析可知， $x$ 为 $2sum[i]$ ， $y$ 为 $sum[i]^2+f[i]$ )
【终于可以粘代码了】

#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;
const int mn = 500005;
struct point{
    ll x, y;
    int p;
}q[mn];
ll f[mn], s[mn];
int h, t;
inline ll cdot(ll x1, ll x2, ll y1, ll y2)
{
    return x1 * y2 - x2 * y1;
}
int main()
{
    int n, m, i;
    while(~scanf("%d%d", &n, &m))
    {
        for(i = 1; i <= n; i++)
            scanf("%lld", &s[i]), s[i] += s[i-1];
        h = t = 1, f[1] = s[1] * s[1] + m, q[1] = (point){s[1] << 1, s[1] * s[1] + f[1], 1};
        for(i = 2; i <= n; i++)
        {
            f[i] = s[i] * s[i] + m;
            while(t - h > 0 && cdot(q[h].x, s[i] * q[h].x, q[h+1].x - q[h].x, q[h+1].y - q[h].y) <= 0)
                h++;
            f[i] = min(f[i], f[q[h].p] + (s[i] - s[q[h].p]) * (s[i] - s[q[h].p]) + m);
            point tmp = (point) {s[i] << 1, s[i] * s[i] + f[i], i};
            while(t - h > 0 && cdot(q[t].x - q[t-1].x, q[t].y - q[t-1].y, tmp.x - q[t].x, tmp.y - q[t].y) <= 0)
                t--;
            q[++t] = tmp;
        }
        printf("%lld\n", f[n]);
    }
}

【法2】

我们要维护k的单调不下降队列，即队中元素满足：
$\frac{\Delta x_i}{\Delta y_i}≤\frac{\Delta x_{i+1}}{\Delta y_{i+1}}$
交叉相乘：
$\Delta x_i\Delta y_{i+1}≤\Delta x_{i+1}\Delta y_i$
用这个关系维护单调队列即可。
其实，【法2】更简单，运用得更多。若想看看这种方法的运用和实现，看这道题。