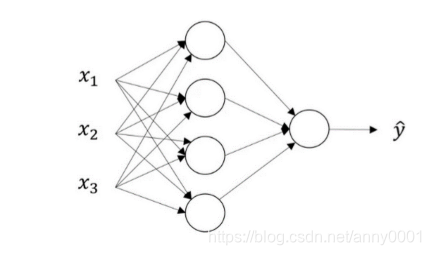
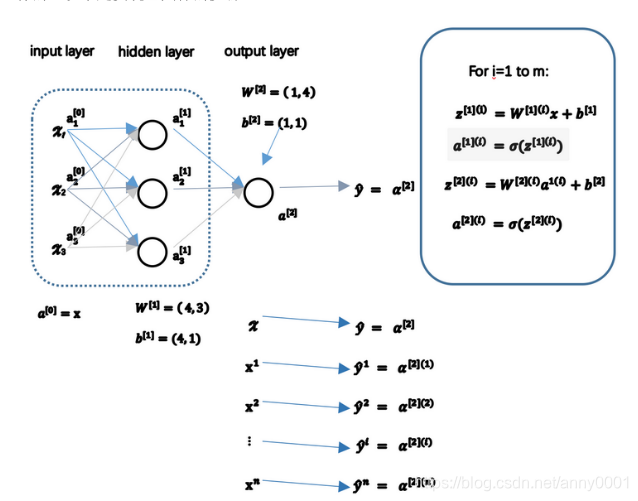
下面是一张神经网络的图片,现在给此图的不同部分约定一些名字
3.2.1
3.2.1
3 . 2 . 1
有一个个体,属性值为:
x
1
,
x
2
,
x
3
x_1,x_2,x_3
x 1 , x 2 , x 3
输入层 :即
x
1
,
x
2
,
x
3
\ x_1,x_2,x_3
x 1 , x 2 , x 3 隐藏层 :上图的四个结点。输出层 :上图的最后一层由一个结点构成
x
x
x
y
y
y
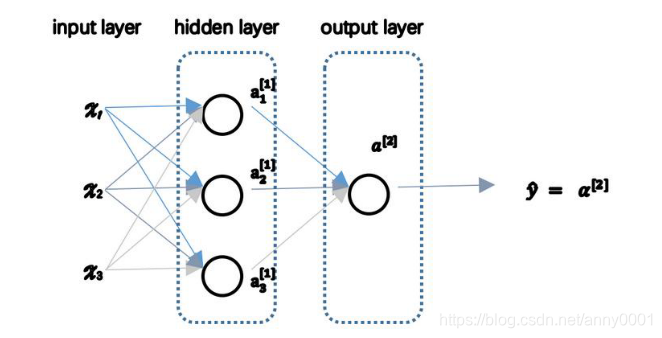
下面引入几个符号:
输入层的激活值,即输入特征
a
[
0
]
a^{[0]}
a [ 0 ]
a
[
0
]
=
[
x
1
x
2
x
3
]
a^{[0]}=\begin{bmatrix} x^1\\x^2\\x^3 \end{bmatrix}
a [ 0 ] = ⎣ ⎡ x 1 x 2 x 3 ⎦ ⎤
隐藏层的激活值,
a
[
1
]
a^{[1]}
a [ 1 ]
a
[
1
]
=
[
a
1
[
1
]
a
2
[
1
]
a
3
[
1
]
a
4
[
1
]
]
a^{[1]}=\begin{bmatrix} a^{[1]}_1\\a^{[1]}_2\\a^{[1]}_3 \\a^{[1]}_4\end{bmatrix}
a [ 1 ] = ⎣ ⎢ ⎢ ⎢ ⎡ a 1 [ 1 ] a 2 [ 1 ] a 3 [ 1 ] a 4 [ 1 ] ⎦ ⎥ ⎥ ⎥ ⎤
输出层,
y
^
\hat y
y ^
y
^
=
a
[
2
]
\hat y = a^{[2]}
y ^ = a [ 2 ]
3.2.2
3.2.2
3 . 2 . 2
a
4
[
1
]
a_4^{[1]}
a 4 [ 1 ]
W
W
W
b
b
b
[
1
]
\ ^{[1]}
[ 1 ]
W
[
1
]
W^{[1]}
W [ 1 ]
W
[
1
]
=
[
w
1
[
1
]
w
1
[
2
]
w
1
[
3
]
w
1
[
4
]
w
2
[
1
]
w
2
[
2
]
w
2
[
3
]
w
2
[
4
]
w
3
[
1
]
w
3
[
2
]
w
3
[
3
]
w
3
[
4
]
]
W^{[1]} = \begin{bmatrix} w_1^{[ 1 ]}\ \ w_1^{[2 ]}\ \ w_1^{[ 3 ]}\ \ w_1^{[4 ]} \\ \\ w_2^{[ 1 ]}\ \ w_2^{[ 2 ]}\ \ w_2^{[3 ]}\ \ w_2^{[ 4 ]} \\ \\ w_3^{[ 1 ]}\ \ w_3^{[2 ]}\ \ w_3^{[ 3 ]}\ \ w_3^{[ 4 ]} \end{bmatrix}
W [ 1 ] = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ w 1 [ 1 ] w 1 [ 2 ] w 1 [ 3 ] w 1 [ 4 ] w 2 [ 1 ] w 2 [ 2 ] w 2 [ 3 ] w 2 [ 4 ] w 3 [ 1 ] w 3 [ 2 ] w 3 [ 3 ] w 3 [ 4 ] ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
b
[
1
]
b^{[1]}
b [ 1 ]
b
[
1
]
=
[
b
1
b
2
b
3
b
4
]
b^{[1]} = \begin{bmatrix} b_1 \\ b_2\\ b_3\\ b_4 \end{bmatrix}
b [ 1 ] = ⎣ ⎢ ⎢ ⎡ b 1 b 2 b 3 b 4 ⎦ ⎥ ⎥ ⎤
类似的输出层也有其关联的参数:
W
[
2
]
W^{[2]}
W [ 2 ]
b
[
2
]
b^{[2]}
b [ 2 ]
上一节介绍了只有一个隐层的神经网络的结构与符号表示,现在我们来看这个神经网络是如何计算输出
y
^
\hat y
y ^
3.3.1
3.3.1
3 . 3 . 1
x
x
x
a
a
a
W
W
W
3.3.2
3.3.2
3 . 3 . 2
z
z
z
a
a
a
z
1
[
1
]
=
w
1
[
1
]
T
x
+
b
1
[
1
]
z^{[1]}_1 = {w^{[1]}_1}^{T}x\ + \ b_1^{[1]}
z 1 [ 1 ] = w 1 [ 1 ] T x + b 1 [ 1 ]
a
1
[
1
]
=
σ
(
z
1
[
1
]
)
a^{[1]}_1 = \sigma(z_1^{[1]})
a 1 [ 1 ] = σ ( z 1 [ 1 ] )
z
1
[
1
]
=
w
1
[
1
]
T
x
+
b
1
[
1
]
,
a
1
[
1
]
=
σ
(
z
1
[
1
]
)
z^{[1]}_1 = {w^{[1]}_1}^{T}x\ + \ b_1^{[1]},\ \ a_1^{[1]}=\sigma(z_1^{[1]})
z 1 [ 1 ] = w 1 [ 1 ] T x + b 1 [ 1 ] , a 1 [ 1 ] = σ ( z 1 [ 1 ] )
z
2
[
1
]
=
w
2
[
1
]
T
x
+
b
2
[
1
]
,
a
2
[
1
]
=
σ
(
z
2
[
1
]
)
z^{[1]}_2 = {w^{[1]}_2}^{T}x\ + \ b_2^{[1]},\ \ a_2^{[1]}=\sigma(z_2^{[1]})
z 2 [ 1 ] = w 2 [ 1 ] T x + b 2 [ 1 ] , a 2 [ 1 ] = σ ( z 2 [ 1 ] )
z
3
[
1
]
=
w
3
[
1
]
T
x
+
b
3
[
1
]
,
a
3
[
1
]
=
σ
(
z
3
[
1
]
)
z^{[1]}_3 = {w^{[1]}_3}^{T}x\ + \ b_3^{[1]},\ \ a_3^{[1]}=\sigma(z_3^{[1]})
z 3 [ 1 ] = w 3 [ 1 ] T x + b 3 [ 1 ] , a 3 [ 1 ] = σ ( z 3 [ 1 ] )
z
4
[
1
]
=
w
4
[
1
]
T
x
+
b
4
[
1
]
,
a
4
[
1
]
=
σ
(
z
4
[
1
]
)
z^{[1]}_4 = {w^{[1]}_4}^{T}x\ + \ b_4^{[1]},\ \ a_4^{[1]}=\sigma(z_4^{[1]})
z 4 [ 1 ] = w 4 [ 1 ] T x + b 4 [ 1 ] , a 4 [ 1 ] = σ ( z 4 [ 1 ] )
隐层计算:
[
z
1
[
1
]
z
2
[
1
]
z
3
[
1
]
z
4
[
1
]
]
=
[
w
1
[
1
]
w
1
[
2
]
w
1
[
3
]
w
2
[
1
]
w
2
[
2
]
w
2
[
3
]
w
3
[
1
]
w
3
[
2
]
w
3
[
3
]
w
4
[
1
]
w
4
[
2
]
w
4
[
3
]
]
⏞
W
[
1
]
∗
[
x
1
x
2
x
3
]
⏞
i
n
p
u
t
+
[
b
1
[
1
]
b
2
[
1
]
b
3
[
1
]
b
4
[
1
]
]
⏞
b
[
1
]
\begin{bmatrix}z^{[1]}_1 \\ \\ z^{[1]}_2\\ \\ z^{[1]}_3\\ \\z^{[1]}_4 \end{bmatrix}= \overbrace{\begin{bmatrix} w_1^{[ 1 ]}\ \ w_1^{[2 ]}\ \ w_1^{[ 3 ]} \\ \\ w_2^{[ 1 ]}\ \ w_2^{[ 2 ]}\ \ w_2^{[3 ]}\\ \\ w_3^{[ 1 ]}\ \ w_3^{[2 ]}\ \ w_3^{[ 3 ]} \\ \\ w_4^{[ 1 ]}\ \ w_4^{[ 2 ]}\ \ w_4^{[3 ]} \end{bmatrix}}^{W^{[1]}} * \overbrace{\begin{bmatrix}x_1 \\ \\ x_2\\ \\ x_3\\ \end{bmatrix}}^{input} + \overbrace{\begin{bmatrix}b^{[1]}_1 \\ \\ b^{[1]}_2\\ \\ b^{[1]}_3\\ \\b^{[1]}_4 \end{bmatrix}}^{b^{[1]}}
⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ z 1 [ 1 ] z 2 [ 1 ] z 3 [ 1 ] z 4 [ 1 ] ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ w 1 [ 1 ] w 1 [ 2 ] w 1 [ 3 ] w 2 [ 1 ] w 2 [ 2 ] w 2 [ 3 ] w 3 [ 1 ] w 3 [ 2 ] w 3 [ 3 ] w 4 [ 1 ] w 4 [ 2 ] w 4 [ 3 ] ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
W [ 1 ] ∗ ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ x 1 x 2 x 3 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤
i n p u t + ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ b 1 [ 1 ] b 2 [ 1 ] b 3 [ 1 ] b 4 [ 1 ] ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
b [ 1 ]
a
[
1
]
=
[
a
1
[
1
]
a
2
[
1
]
a
3
[
1
]
a
4
[
1
]
]
=
σ
(
[
z
1
[
1
]
z
2
[
1
]
z
3
[
1
]
z
4
[
1
]
]
⏞
z
[
1
]
)
a^{[1]} = \begin{bmatrix} a^{[1]}_1 \\ \\ a^{[1]}_2\\ \\ a^{[1]}_3\\ \\a^{[1]}_4 \end{bmatrix} = \sigma \begin{pmatrix}\overbrace{\begin{bmatrix}z^{[1]}_1 \\ \\ z^{[1]}_2\\ \\ z^{[1]}_3\\ \\z^{[1]}_4 \end{bmatrix}}^{z^{[1]}} \end{pmatrix}
a [ 1 ] = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ a 1 [ 1 ] a 2 [ 1 ] a 3 [ 1 ] a 4 [ 1 ] ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = σ ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ z 1 [ 1 ] z 2 [ 1 ] z 3 [ 1 ] z 4 [ 1 ] ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
z [ 1 ] ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞
输出层计算(参考逻辑回归,即单个神经元的计算):
y
^
=
a
[
2
]
=
σ
(
z
[
2
]
)
=
σ
(
W
[
2
]
T
a
[
1
]
+
b
[
2
]
)
\hat y = a^{[2]}=\sigma(z^{[2]})= \sigma({W^{[2]}}^{T}a^{[1]}+b^{[2]})
y ^ = a [ 2 ] = σ ( z [ 2 ] ) = σ ( W [ 2 ] T a [ 1 ] + b [ 2 ] )
前面一节讲了单一训练个体的神经网络的输出值计算,下面讲多训练个体,并计算出结果。
3.4.1
3.4.1
3 . 4 . 1
对于一个给定的输入特征向量
x
x
x
y
^
\hat y
y ^
x
(
1
)
=
[
x
1
(
1
)
x
2
(
1
)
⋮
x
n
(
1
)
]
x^{(1)}=\begin{bmatrix}x_1^{(1)}\\ x_2^{(1)}\\\vdots\\x_n^{(1)} \end{bmatrix}
x ( 1 ) = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ x 1 ( 1 ) x 2 ( 1 ) ⋮ x n ( 1 ) ⎦ ⎥ ⎥ ⎥ ⎥ ⎤
y
^
\hat y
y ^
x
(
2
)
x^{(2)}
x ( 2 )
y
^
(
2
)
\hat y^{(2)}
y ^ ( 2 )
x
(
m
)
x^{(m)}
x ( m )
y
^
(
m
)
\hat y^{(m)}
y ^ ( m )
3.4.1
3.4.1
3 . 4 . 1
y
^
(
1
)
=
a
[
2
]
(
1
)
\hat y^{(1)}=a^{[2](1)}
y ^ ( 1 ) = a [ 2 ] ( 1 )
y
^
(
2
)
=
a
[
2
]
(
2
)
\hat y^{(2)}=a^{[2](2)}
y ^ ( 2 ) = a [ 2 ] ( 2 )
⋮
\vdots
⋮
y
^
(
m
)
=
a
[
2
]
(
m
)
\hat y^{(m)}=a^{[2](m)}
y ^ ( m ) = a [ 2 ] ( m )
a
[
2
]
(
m
)
a^{[2](m)}
a [ 2 ] ( m )
(
i
)
(i)
( i )
(
i
)
(i)
( i )
[
2
]
[2]
[ 2 ]
(
i
)
(i)
( i )
z
[
1
]
(
i
)
=
W
[
1
]
(
i
)
x
(
i
)
+
b
[
1
]
(
i
)
a
[
1
]
(
i
)
=
σ
(
z
[
1
]
(
i
)
)
z^{[1](i)}=W^{[1](i)}x^{(i)}+b^{[1](i)} \\ a^{[1](i)}=\sigma(z^{[1](i)})
z [ 1 ] ( i ) = W [ 1 ] ( i ) x ( i ) + b [ 1 ] ( i ) a [ 1 ] ( i ) = σ ( z [ 1 ] ( i ) )
z
[
2
]
(
i
)
=
W
[
2
]
(
i
)
a
[
1
]
(
i
)
+
b
[
2
]
(
i
)
a
[
2
]
(
i
)
=
σ
(
z
[
2
]
(
i
)
)
z^{[2](i)}=W^{[2](i)}a^{[1](i)}+b^{[2](i)} \\a^{[2](i)}=\sigma(z^{[2](i)})
z [ 2 ] ( i ) = W [ 2 ] ( i ) a [ 1 ] ( i ) + b [ 2 ] ( i ) a [ 2 ] ( i ) = σ ( z [ 2 ] ( i ) )
x
=
[
⋮
x
(
1
)
⋮
⋮
x
(
2
)
⋮
⋮
…
⋮
⋮
x
(
m
)
⋮
]
x = \begin{bmatrix} \begin{matrix}\vdots\\x^{(1)} \\ \vdots\end{matrix} \begin{matrix}\vdots\\\ x^{(2)}\ \\ \vdots\end{matrix} \begin{matrix}\vdots\\\ \dots\ \\ \vdots\end{matrix} \begin{matrix}\vdots\\x^{(m)} \\ \vdots\end{matrix} \end{bmatrix}
x = ⎣ ⎢ ⎢ ⎡ ⋮ x ( 1 ) ⋮ ⋮ x ( 2 ) ⋮ ⋮ … ⋮ ⋮ x ( m ) ⋮ ⎦ ⎥ ⎥ ⎤
Z
[
1
]
=
[
⋮
z
[
1
]
(
1
)
⋮
⋮
z
[
1
]
(
2
)
⋮
⋮
…
⋮
⋮
z
[
1
]
(
m
)
⋮
]
Z^{[1]} = \begin{bmatrix} \begin{matrix}\vdots\\z^{[1](1)} \\ \vdots\end{matrix} \begin{matrix}\vdots\\\ z^{[1](2)}\ \\ \vdots\end{matrix} \begin{matrix}\vdots\\\ \dots\ \\ \vdots\end{matrix} \begin{matrix}\vdots\\\ z^{[1](m)} \\ \vdots\end{matrix} \end{bmatrix}
Z [ 1 ] = ⎣ ⎢ ⎢ ⎡ ⋮ z [ 1 ] ( 1 ) ⋮ ⋮ z [ 1 ] ( 2 ) ⋮ ⋮ … ⋮ ⋮ z [ 1 ] ( m ) ⋮ ⎦ ⎥ ⎥ ⎤
A
[
1
]
=
[
⋮
a
[
1
]
(
1
)
⋮
⋮
a
[
1
]
(
2
)
⋮
⋮
…
⋮
⋮
a
[
1
]
(
m
)
⋮
]
A^{[1]} = \begin{bmatrix} \begin{matrix}\vdots\\a^{[1](1)} \\ \vdots\end{matrix} \begin{matrix}\vdots\\\ a^{[1](2)}\ \\ \vdots\end{matrix} \begin{matrix}\vdots\\\ \dots\ \\ \vdots\end{matrix} \begin{matrix}\vdots\\\ a^{[1](m)} \\ \vdots\end{matrix} \end{bmatrix}
A [ 1 ] = ⎣ ⎢ ⎢ ⎡ ⋮ a [ 1 ] ( 1 ) ⋮ ⋮ a [ 1 ] ( 2 ) ⋮ ⋮ … ⋮ ⋮ a [ 1 ] ( m ) ⋮ ⎦ ⎥ ⎥ ⎤
Z
[
2
]
=
W
[
2
]
A
[
1
]
+
b
[
2
]
Z^{[2]} = W^{[2]}A^{[1]}+b^{[2]}
Z [ 2 ] = W [ 2 ] A [ 1 ] + b [ 2 ]
A
[
2
]
=
σ
(
z
[
2
]
)
A^{[2]}=\sigma(z^{[2]})
A [ 2 ] = σ ( z [ 2 ] )
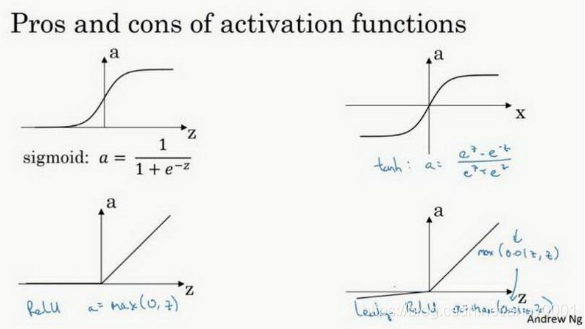
表达式:
(3.6.1)
a
=
σ
(
z
)
=
1
1
+
e
−
z
a= \sigma(z)=\frac{1}{1+e^{-z}}\tag{3.6.1}
a = σ ( z ) = 1 + e − z 1 ( 3 . 6 . 1 )
导数:
(3.6.2)
σ
′
(
z
)
=
a
(
1
−
a
)
\sigma'(z)=a(1-a)\tag{3.6.2}
σ ′ ( z ) = a ( 1 − a ) ( 3 . 6 . 2 )
表达式:
(3.6.3)
a
=
t
a
n
h
(
z
)
=
e
z
−
e
−
z
e
z
+
e
−
z
a=tanh(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}\tag{3.6.3}
a = t a n h ( z ) = e z + e − z e z − e − z ( 3 . 6 . 3 )
导数:
(3.6.4)
t
a
n
h
′
(
z
)
=
1
−
a
2
tanh'(z)=1-a^2\tag{3.6.4}
t a n h ′ ( z ) = 1 − a 2 ( 3 . 6 . 4 )
表达式:
(3.6.5)
a
=
^
g
(
z
)
=
m
a
x
(
0
,
z
)
a\ \hat =\ g(z)= max(0,z)\tag{3.6.5}
a = ^ g ( z ) = m a x ( 0 , z ) ( 3 . 6 . 5 )
(3.6.6)
g
′
(
z
)
=
{
1
,
if
z
> 0
0
,
if
z
<0
g'(z) = \begin{cases} 1, & \text{if $z$> 0 }\\[2ex] 0, & \text{if $z$<0} \end{cases} \tag{3.6.6}
g ′ ( z ) = ⎩ ⎨ ⎧ 1 , 0 , if z > 0 if z <0 ( 3 . 6 . 6 )
表达式:
(3.6.7)
a
=
^
g
(
z
)
=
m
a
x
(
0.01
z
,
z
)
a\ \hat =\ g(z)=max(0.01z,z)\tag{3.6.7}
a = ^ g ( z ) = m a x ( 0 . 0 1 z , z ) ( 3 . 6 . 7 )
(3.6.8)
g
′
(
z
)
=
{
1
,
if
z
> 0
0.01
,
if
z
<0
u
n
d
e
f
i
n
e
d
,
if
z
=0
when
z
= 0,
g
′
could be defined as 1 or 0.01, case of
z
=
0
seldomly occur
g'(z) = \begin{cases} 1, & \text{if $z$> 0 }\\[2ex] 0.01, & \text{if $z$<0}\\[2ex] undefined,&\text{if $z$=0} \end{cases} \text{when $z$ = 0, $g'$ could be defined as 1 or 0.01, case of $z=0$ seldomly occur} \tag{3.6.8}
g ′ ( z ) = ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ 1 , 0 . 0 1 , u n d e f i n e d , if z > 0 if z <0 if z =0 when z = 0, g ′ could be defined as 1 or 0.01, case of z = 0 seldomly occur ( 3 . 6 . 8 )
如果你是用线性激活函数或者叫恒等激励函数,那么神经网络只是把输入线性组合再输出。事实上,如果你使用线性激活函数或者没有使用一个激活函数,那么无论你的神经网络有多少层,你一直在做的只是计算线性函数,那样就相当于直接去掉全部隐藏层,直接线性相加就行了,即如果你在隐藏层用线性激活函数,在输出层用 sigmoid 函数,那么这个模型的复杂度和没有任何隐藏层的标准 Logistic 回归是一样的,如果你愿意的话,可以证明一下。在这里线性隐层一点用也没有,因为这两个线性函数的组合本身就是线性函数,所以除非你引入非线性,否则你无法计算更有趣的函数,即使你的网络层数再多也不行
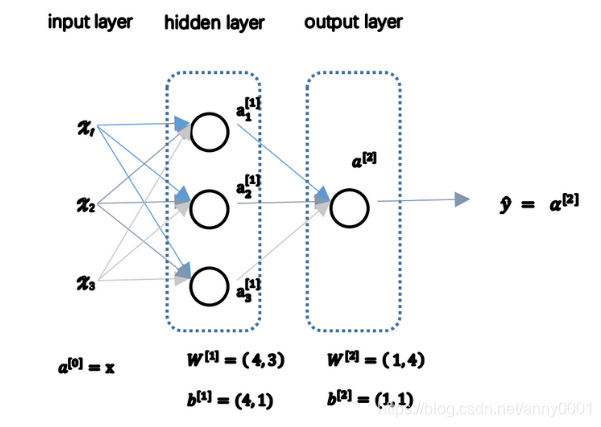
单隐层神经网络会有
W
[
1
]
W^{[1]}
W [ 1 ]
b
[
1
]
b^{[1]}
b [ 1 ]
W
[
2
]
W^{[2]}
W [ 2 ]
b
[
2
]
b^{[2]}
b [ 2 ]
n
x
n_x
n x
n
[
1
]
n^{[1]}
n [ 1 ]
n
[
2
]
n^{[2]}
n [ 2 ]
W
[
1
]
W^{[1]}
W [ 1 ]
(
n
[
1
]
,
n
[
0
]
)
(n^{[1]},n^{[0]})
( n [ 1 ] , n [ 0 ] )
b
[
1
]
b^{[1]}
b [ 1 ]
n
[
1
]
n^{[1]}
n [ 1 ]
(
n
[
1
]
,
1
)
(n^{[1]},1)
( n [ 1 ] , 1 )
W
[
2
]
W^{[2]}
W [ 2 ]
(
n
[
2
]
,
n
[
1
]
)
(n^{[2]},n^{[1]})
( n [ 2 ] , n [ 1 ] )
b
[
2
]
b^{[2]}
b [ 2 ]
(
n
[
2
]
,
1
)
(n^{[2]},1)
( n [ 2 ] , 1 )
J
(
W
[
1
]
,
b
[
1
]
,
W
[
2
]
,
b
[
12
]
)
=
1
m
∑
i
=
1
n
L
(
y
^
,
y
)
J(W^{[1]},b^{[1]}, W^{[2]} ,b^{[12]})=\frac{1}{m}\sum^n_{i=1}L(\hat y , y)
J ( W [ 1 ] , b [ 1 ] , W [ 2 ] , b [ 1 2 ] ) = m 1 ∑ i = 1 n L ( y ^ , y )
y
^
(
i
)
,
(
i
=
1
,
2
,
.
.
.
,
m
)
\hat{y}^{(i)},(i=1,2,...,m)
y ^ ( i ) , ( i = 1 , 2 , . . . , m )
(3.9.1)
d
W
[
1
]
=
d
J
d
W
[
1
]
,
d
b
[
1
]
=
d
J
d
b
[
1
]
dW^{[1]}=\frac{dJ}{dW^{[1]}},\ db^{[1]}=\frac{dJ}{db^{[1]}}\tag{3.9.1}
d W [ 1 ] = d W [ 1 ] d J , d b [ 1 ] = d b [ 1 ] d J ( 3 . 9 . 1 )
(3.9.2)
d
W
[
2
]
=
d
J
d
W
[
2
]
,
d
b
[
2
]
=
d
J
d
b
[
2
]
dW^{[2]}=\frac{dJ}{dW^{[2]}},\ db^{[2]}=\frac{dJ}{db^{[2]}}\tag{3.9.2}
d W [ 2 ] = d W [ 2 ] d J , d b [ 2 ] = d b [ 2 ] d J ( 3 . 9 . 2 )
(3.9.3)
W
[
1
]
:
=
W
[
1
]
−
α
d
W
[
1
]
,
b
[
1
]
:
=
b
[
1
]
−
α
d
b
[
1
]
W^{[1]}:=W^{[1]}-\alpha dW^{[1]},\ b^{[1]}:=b^{[1]}-\alpha db^{[1]}\tag{3.9.3}
W [ 1 ] : = W [ 1 ] − α d W [ 1 ] , b [ 1 ] : = b [ 1 ] − α d b [ 1 ] ( 3 . 9 . 3 )
(3.9.3)
W
[
2
]
:
=
W
[
2
]
−
α
d
W
[
2
]
,
b
[
2
]
:
=
b
[
2
]
−
α
d
b
[
2
]
W^{[2]}:=W^{[2]}-\alpha dW^{[2]},\ b^{[2]}:=b^{[2]}-\alpha db^{[2]}\tag{3.9.3}
W [ 2 ] : = W [ 2 ] − α d W [ 2 ] , b [ 2 ] : = b [ 2 ] − α d b [ 2 ] ( 3 . 9 . 3 )
正向传播4个方程:
z
[
1
]
=
W
[
1
]
x
+
b
[
1
]
z^{[1]}=W^{[1]}x+b^{[1]}
z [ 1 ] = W [ 1 ] x + b [ 1 ]
a
[
1
]
=
σ
(
z
[
1
]
)
a^{[1]}=\sigma(z^{[1]})
a [ 1 ] = σ ( z [ 1 ] )
z
[
2
]
=
W
[
2
]
a
[
1
]
+
b
[
2
]
z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}
z [ 2 ] = W [ 2 ] a [ 1 ] + b [ 2 ]
a
[
2
]
=
g
[
2
]
(
z
[
2
]
)
=
σ
(
z
[
2
]
)
a^{[2]}=g^{[2]}(z^{[2]})=\sigma(z^{[2]})
a [ 2 ] = g [ 2 ] ( z [ 2 ] ) = σ ( z [ 2 ] )
反向传播6个方程:
(3.9.4)
d
z
[
1
]
=
A
[
2
]
−
Y
,
Y
=
[
y
(
1
)
,
y
(
2
)
,
…
,
y
(
m
)
]
dz^{[1]}=A^{[2]}-Y,\ Y=[y^{(1)},y^{(2)},\dots,y^{(m)}]\tag{3.9.4}
d z [ 1 ] = A [ 2 ] − Y , Y = [ y ( 1 ) , y ( 2 ) , … , y ( m ) ] ( 3 . 9 . 4 )
(3.9.5)
d
W
[
2
]
=
1
m
d
z
[
2
]
(
A
[
1
]
)
T
dW^{[2]}=\frac{1}{m}dz^{[2]}(A^{[1]})^T\tag{3.9.5}
d W [ 2 ] = m 1 d z [ 2 ] ( A [ 1 ] ) T ( 3 . 9 . 5 )
(3.9.6)
d
b
[
2
]
=
1
m
n
p
.
s
u
m
(
d
z
[
2
]
,
a
x
i
s
=
1
,
k
e
e
p
d
i
m
s
=
T
r
u
e
)
db^{[2]}= \frac{1}{m}np.sum(dz^{[2]},axis=1,keepdims=True) \tag{3.9.6}
d b [ 2 ] = m 1 n p . s u m ( d z [ 2 ] , a x i s = 1 , k e e p d i m s = T r u e ) ( 3 . 9 . 6 )
(3.9.7)
d
z
[
1
]
=
(
W
[
2
]
)
T
d
z
[
2
]
⎵
(
n
[
1
]
,
m
)
⋅
(
g
[
1
]
)
′
⏞
hidden layer’s activation function
⋅
(
z
[
1
]
)
⎵
(
n
[
1
]
,
m
)
dz^{[1]}= \underbrace{(W^{[2]})^Tdz^{[2]}}_{(n^{[1]},m)} \cdot \overbrace{(g^{[1]})'}^{\text{hidden layer's activation function} } \cdot \underbrace{(z^{[1]})}_{(n^{[1]},m)} \tag{3.9.7}
d z [ 1 ] = ( n [ 1 ] , m )
( W [ 2 ] ) T d z [ 2 ] ⋅ ( g [ 1 ] ) ′
hidden layer’s activation function ⋅ ( n [ 1 ] , m )
( z [ 1 ] ) ( 3 . 9 . 7 )
(3.9.8)
d
W
[
1
]
=
1
m
d
z
[
1
]
x
T
dW^{[1]}=\frac{1}{m}dz^{[1]}x^T \tag{3.9.8}
d W [ 1 ] = m 1 d z [ 1 ] x T ( 3 . 9 . 8 )
(3.9.9)
d
b
[
1
]
⎵
(
n
[
1
]
,
1
)
=
1
m
⋅
n
p
.
s
u
m
(
d
z
[
1
]
,
a
x
i
s
=
1
,
k
e
e
p
d
i
m
s
=
T
r
u
e
)
\underbrace{db^{[1]}}_{(n^{[1]},1 )}=\frac{1}{m}\cdot np.sum(dz^{[1]},axis=1,keepdims=True)\tag{3.9.9}
( n [ 1 ] , 1 )
d b [ 1 ] = m 1 ⋅ n p . s u m ( d z [ 1 ] , a x i s = 1 , k e e p d i m s = T r u e ) ( 3 . 9 . 9 )
上述是反向传播的步骤,且这些都是针对所有样本进行过向量化的,Y是1xm的矩阵,np.sum是python的numpy命令,axis=1表示水平相加求和,keepdims是防止python输出那些古怪的秩数组(n,),加上这个确保
d
b
[
i
]
db^{[i]}
d b [ i ]
(
W
[
2
]
d
z
[
2
]
)
(W^{[2]}dz^{[2]})
( W [ 2 ] d z [ 2 ] )
(
z
[
2
]
)
(z^{[2]})
( z [ 2 ] )
(
n
[
1
]
,
m
)
(n^{[1]},m)
( n [ 1 ] , m )
初始化不能为0,如果初始化为0,那么梯度下降将不起作用。
让我们继续探讨一下。有两个输入特征,
n
[
0
]
=
2
n^{[0]}=2
n [ 0 ] = 2
n
[
1
]
n^{[1]}
n [ 1 ]
W
[
1
]
W^{[1]}
W [ 1 ] 2 的矩阵,假设把它初始化为 0 的 2 2 矩阵,
b
[
1
]
b^{[1]}
b [ 1 ]
(
0
,
0
)
T
(0,0)^{T}
( 0 , 0 ) T
W
W
W
a
1
[
1
]
a^{[1]}_1
a 1 [ 1 ]
a
2
[
1
]
a^{[1]}_2
a 2 [ 1 ]
d
z
1
[
1
]
dz^{[1]}_1
d z 1 [ 1 ]
d
z
2
[
2
]
dz^{[2]}_2
d z 2 [ 2 ]
W
[
2
]
W^{[2]}
W [ 2 ]
W
W
W
 图
图
 图
图
图
图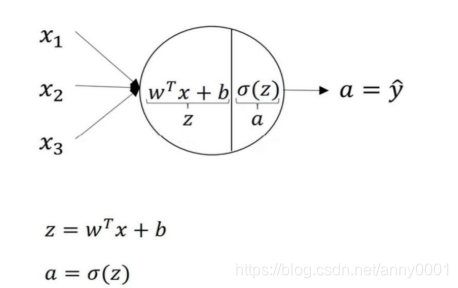 图
图
 图
图