搬运自我的CSDN https://blog.csdn.net/u013213111/article/details/89890114
参考Homogeneous Coordinates ,Michigan Technological University 的 Dr. C.-K. Shene写的Introduction to Computing with Geometry Tutorial之中的一部分,摘录+翻译。
引入齐次坐标系的原因之一是为了描述infinity(无穷远点)。
One of the many purposes of using homogeneous coordinates is to capture the concept of infinity. In the Euclidean coordinate system, infinity is something that does not exist. Mathematicians have discovered that many geometric concepts and computations can be greatly simplified if the concept of infinity is used. This will become very clear when we move to curves and surfaces design. Without the use of homogeneous coordinates system, it would be difficult to design certain classes of very useful curves and surfaces in computer graphics and computer-aided design.
首先考虑两个实数a和w,计算a/w的值。保持a不变,当w变小时,a/w的值变大。那么当w为0时,a/w就会变为infinity(无穷大)。因此“无穷大”可以用一个数对(a, w)或者商a/w来描述,(a, 0)即为无穷大。
Let us consider two real numbers, a and w, and compute the value of a/w. Let us hold the value of a fixed and vary the value of w. As w getting smaller, the value of a/w is getting larger. If w approaches zero, a/w approaches to infinity! Thus, to capture the concept of infinity, we use two numbers a and w to represent a value v, v=a/w. If w is not zero, the value is exactly a/w. Otherwise, we identify the infinite value with (a,0). Therefore, the concept of infinity can be represented with a number pair like (a, w) or as a quotient a/w.
推广到xy平面坐标系中,将x和y分别用x/w和y/w代替。例如多项式函数 f(x,y)=0 就会变为 f(x/w,y/w)=0。假如 f(x,y)=0 是一个n次多项式,那么将其乘 wn 就会消掉所有的分母。
Let us apply this to the xy-coordinate plane. If we replace x and y with x/w and y/w, a function f(x,y)=0 becomes f(x/w,y/w)=0. If function f(x,y) = 0 is a polynomial, multiplying it with wn will clear all denominators, where n is the degree of the polynomial.
举个栗子:
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0,那么将x和y分别用x/w和y/w代替后,再乘w2,得到 Ax2 + 2Bxy + Cy2 + 2Dxw + 2Eyw + Fw2 = 0,每一项(i.e., x2, xy, y2, xw, yw 和 w2) 均为二次项。
Let the given equation be a second degree polynomial Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0. After replacing x and y with x/w and y/w and multiplying the result with w2, we have Ax2 + 2Bxy + Cy2 + 2Dxw + 2Eyw + Fw2 = 0 ,If you look at these two polynomials carefully, you will see that the degrees of all terms are equal. In the case of a line, terms x, y and w are of degree one, while in the second degree polynomial, all terms (i.e., x2, xy, y2, xw, yw and w2) are of degree two.
对于一个n次多项式,引入w之后,所有项均变为n次项。这些变换后的多项式就是齐次多项式,而坐标系(x,y,w)就是齐次坐标系。
Given a polynomial of degree n, after introducing w, all terms are of degree n. Consequently, these polynomials are called homogeneous polynomials and the coordinates (x,y,w) the homogeneous coordinates.
齐次坐标系中的点(x,y,w),在xy坐标系中对应的点为(x/w,y/w)。
Given a point (x,y,w) in homogeneous coordinates, what is its corresponding point in the xy-plane? From what we discussed for converting a homogeneous polynomial back to its conventional form, you might easily guess that the answer must be (x/w,y/w). This is correct. Thus, a point (3,4,5) in homogeneous coordinates converts to point (3/5,4/5)=(0.6,0.8) in the xy-plane. Similarly, a point (x,y,z,w) in homogeneous coordinates converts to a point (x/w,y/w,z/w) in space.
那么,xy坐标系中的点(x,y)对应齐次坐标系中的点是?
是(xw,yw,w),其中w可以是任意的非零数。
注意:将齐次坐标系中的点映射到传统坐标系中是唯一的,而将传统坐标系中的点映射到齐次坐标系中则不是唯一的。
Conversely, what is the homogeneous coordinates of a point (x,y) in the xy-plane? It is simply (x,y,1)! That is, let the w component be 1. In fact, this is only part of the story, because the answer is not unique. The homogeneous coordinates of a point (x,y) in the xy-plane is (xw, yw, w) for any non-zero w. Why is this true? Because (xw, yw, w) is converted back to (x,y). As a result, the following is important for you to memorize:
Converting from a homogeneous coordinates to a conventional one is unique; but, converting a conventional coordinates to a homogeneous one is not.
For example, a point (4,2,3) in space is convert to (4w, 2w, 3w, w) for any non-zero w.
再回头看看无穷远点的概念。将一个固定的点(x,y)乘1/w从而映射到齐次坐标系中,得到对应的点(x/w,y/w,1/w)。当w变为0时,(x/w,y/w)移动到无穷远处。因此,齐次坐标系中的点(x,y,0)称为ideal point或者在(x,y)方向上的无穷远点。
As mentioned at the very beginning of this page, homogeneous coordinates can easily capture the concept of infinity. Let a point (x,y) be fixed and converted to a homogeneous coordinate by multiplying with 1/w, (x/w,y/w,1/w). Let the value of w approach to zero, then (x/w,y/w) moves farther and farther away in the direction of (x,y). When w becomes zero, (x/w,y/w) moves to infinity. Therefore, we would say, the homogeneous coordinate (x,y,0) is the ideal point or point at infinity in the direction of (x,y).
再举个栗子:
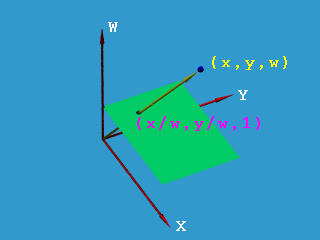
Given a homogeneous coordinate (x,y,w) of a point in the xy-plane, let us consider (x,y,w) to be a point in space whose coordinate values are x, y and w for the x-, y- and w- axes, respectively. The line joining this point and the coordinate origin intersects the plane w = 1 at a point (x/w, y/w, 1).
This transformation treats a two-dimensional homogeneous point as a point in three-dimensional space and projects (from the coordinate origin) this three-dimensional point to the plane w=1. Therefore, as a homogeneous point moves on a curve defined by homogeneous polynomial f(x,y,w)=0, its corresponding point moves in three-dimensional space, which, in turn, is projected to the plane w=1. Of course, (x/w,y/w) moves on a curve in plane w=1.
The above figure also shows clearly that while the conversion from the conventional Euclidean coordinates to homogeneous coordinates is unique, the opposite direction is not because all points on the line joining the origin and (x,y,w) will be projected to (x/w,y/w,1).
另外一些不错的资料:
斯坦福Computer Graphics Lab
CMU Computer Vision
《CV中的多视图几何》——相机模型与标定