为什么叫齐次坐标系?
齐次坐标系,英文名称Homogeneous coordinate system。也就是说Homogeneous国内翻译为“齐次”,查询“齐次”的解释,谷歌翻译Homogeneous是“同质”的意思,百度翻译结果是“均匀的;同性质的,同类的;由相同(或同类型)事物(或人)组成的;[数]齐性的,齐次的”。所以从名字上我们不能顾名思义,只能先理解齐次坐标系在来思考这个名字了。
首先我们先从齐次性开始理解。
齐次性定义
在百度百科里的解释:
以下摘自维基百科对于齐次坐标系的描述:
在数学里,齐次坐标(homogeneous coordinates),或投影坐标(projective coordinates)是指一个用于投影几何里的坐标系统,如同用于欧氏几何里的笛卡儿坐标一般。该词由奥古斯特·费迪南德·莫比乌斯于1827年在其著作《Der barycentrische Calcul》一书内引入[1][2]。齐次坐标可让包括无穷远点的点坐标以有限坐标表示。使用齐次坐标的公式通常会比用笛卡儿坐标表示更为简单,且更为对称。齐次坐标有着广泛的应用,包括电脑图形及3D电脑视觉。使用齐次坐标可让电脑进行仿射变换,并通常,其投影变换能简单地使用矩阵来表示。
实投影平面可以看作是一个具有额外点的欧氏平面,这些点称之为无穷远点,并被认为是位于一条新的线上(该线称之为无穷远线)。每一个无穷远点对应至一个方向(由一条线之斜率给出),可非正式地定义为一个点自原点朝该方向移动之极限。在欧氏平面里的平行线可看成会在对应其共同方向之无穷远点上相交。给定欧氏平面上的一点 (x, y),对任意非零实数 Z,三元组 (xZ, yZ, Z) 即称之为该点的齐次坐标。依据定义,将齐次坐标内的数值乘上同一个非零实数,可得到同一点的另一组齐次坐标。例如,笛卡儿坐标上的点 (1,2) 在齐次坐标中即可标示成 (1,2,1) 或 (2,4,2)。原来的笛卡儿坐标可透过将前两个数值除以第三个数值取回。因此,与笛卡儿坐标不同,一个点可以有无限多个齐次坐标表示法。
一条通过原点 (0, 0) 的线之方程可写作 nx + my = 0,其中 n 及 m 不能同时为 0。以参数表示,则能写成 x = mt, y = − nt。令 Z=1/t,则线上的点之笛卡儿坐标可写作 (m/Z, − n/Z)。在齐次坐标下,则写成 (m, − n, Z)。当 t 趋向无限大,亦即点远离原点时,Z 会趋近于 0,而该点的齐次坐标则会变成 (m, −n, 0)。因此,可定义 (m, −n, 0) 为对应 nx + my = 0 这条线之方向的无穷远点之齐次坐标。因为欧氏平面上的每条线都会与透过原点的某一条线平行,且因为平行线会有相同的无穷远点,欧氏平面每条线上的无穷远点都有其齐次坐标。
概括来说:
- 投影平面上的任何点都可以表示成一三元组 (X, Y, Z),称之为该点的'齐次坐标或投影坐标,其中 X、Y 及 Z 不全为 0。
- 以齐次坐标表表示的点,若该坐标内的数值全乘上一相同非零实数,仍会表示该点。
- 相反地,两个齐次坐标表示同一点,当且仅当其中一个齐次坐标可由另一个齐次坐标乘上一相同非零常数得取得。
- 当 Z 不为 0,则该点表示欧氏平面上的该 (X/Z, Y/Z)。
- 当 Z 为 0,则该点表示一无穷远点。
- 注意,三元组 (0, 0, 0) 不表示任何点。原点表示为 (0, 0, 1)[3]。
从上面的描述我们知道齐次坐标是用于投影几何里的坐标系统,和平时我们用的笛卡尔坐标系一样,是帮助我们理解宇宙的工具。但因为这是两种不同的坐标系,我们需要跳出笛卡尔坐标系,以更宏观的思维来理解,不然有些场景会让我们困惑。
首先我们把下方的这个投影描述图印在脑海中。
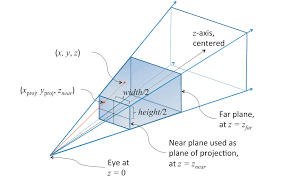
考虑一个点p,它的笛卡尔坐标是(x,y),齐次坐标是(x,y,1),齐次坐标比笛卡尔坐标多一个维度,按照现在书上和网络上的理解基本都是说笛卡尔坐标系就是齐次坐标系中w=1的那个平面,(x,y,1)是齐次坐标(kx,ky,k)表示的点在w=1上的映射。因为一开始我把这个投影想成了正交投影,所以总感觉不对。
那为什么要引入齐次坐标系了?
上面也提到了,主要是方便计算机图形学进行仿射几何变换。简单的理解就是可以使用矩阵同时描述旋转和平移,这样我们就可以使用矩阵相乘来表述物体的旋转、缩放和平移了,具体内容可参照《计算机图形学》等书籍或者网上的资料。
如:https://oncemore.wang/blog/homogeneous/
无穷远的点
使用(∞,∞)?所以在笛卡尔坐标系中无穷远的点是没有定义的。但这个在齐次坐标系统中可以用w=0来表示无穷远的点,即任何(x,y,0)表示无穷远的点。
两条平行线在无限远处相交
笛卡尔坐标系中两条平行线没有交点,即使在三维空间也是,但在齐次坐标系中它们在无穷远点相交。
引申的理解
1.坐标系理解
在笛卡尔坐标系中有一个原点(0,0),对于这个点我以前没有过多的考虑,后来参考了很多资料,有一个说法,想象在宇宙中有一个绝对坐标系,对于我们现在使用的笛卡尔坐标系,其原点位于(a,b)点,当然同时也就还有无数的相同的坐标系,只不过它们的原点不同,对于笛卡尔坐标系中的点(x,y),它对于所有的笛卡尔坐标系都是相同的,有点多维宇宙的感觉,其中一个坐标系就是一个宇宙。我觉得这种思维也很有意思。
2.向量和点
关于向量和点,我觉得下面的这边文章说的很好,大家可以参考。
https://blog.csdn.net/winbobob/article/details/38829001
以下都是我根据这篇博客的得来的感悟。描述一个点比描述一个向量需要更多的信息。我们平时的描述一个点时,其实都忽略了一个信息,即参照点的信息,我们都是基于参照点描述一个点的位置,这个参照点就是原点。下面是我从上面博客截取的一段关于点和向量的一个解释:
对于一个向量v以及基oabc,可以找到一组坐标(v1,v2,v3),使得v = v1 a + v2 b + v3 c (1)
而对于一个点p,则可以找到一组坐标(p1,p2,p3),使得 p – o = p1 a + p2 b + p3 c (2),
从上面对向量和点的表达,我们可以看出为了在坐标系中表示一个点(如p),我们把点的位置看作是对这个基的原点o所进行的一个位移,即一个向量——p – o(有的书中把这样的向量叫做位置向量——起始于坐标原点的特殊向量),我们在表达这个向量的同时用等价的方式表达出了点p:p = o + p1 a + p2 b + p3 c (3)
(1)(3)是坐标系下表达一个向量和点的不同表达方式。这里可以看出,虽然都是用代数分量的形式表达向量和点,但表达一个点比一个向量需要额外的信息。如果我写出一个代数分量表达(1, 4, 7),谁知道它是个向量还是个点!
我们现在把(1)(3)写成矩阵的形式:v = (v1 v2 v3 0) X (a b c o)
p = (p1 p2 p3 1) X (a b c o),这里(a,b,c,o)是坐标基矩阵,右边的列向量分别是向量v和点p在基下的坐标。这样,向量和点在同一个基下就有了不同的表达:3D向量的第4个代数分量是0,而3D点的第4个代数分量是1。像这种这种用4个代数分量表示3D几何概念的方式是一种齐次坐标表示。
上面的推导很完美,但还是有种只知其然的感觉。其实这里有一个非常重要的点没有指出来,就是变换对应矩阵的乘法。这里的变换有平移、旋转、缩放。我们做的这些推导都是想要用矩阵的乘法来表示变换,只有这样上面的推导才不显得突兀。而齐次坐标系的出现,也是处于计算机使用矩阵乘法来表示仿射变换的需求。所以理解齐次坐标系,很重要的一点就是为什么我们需要齐次坐标系。
对于齐次坐标系,我一直想知道它的几何意义,但由于使用欧氏几何的三维空间来理解,总是不得要领。现在觉得,首先我们要明白这些坐标系都是我们理解这个世界的工具,有些工具对于世界的描述很贴合我们对于世界的想象,所以常用,但另外一些工具是从其它的角度来解读这个世界的,在我们使用这些工具之前,我们需要跳出原先的思维(如齐次坐标系再更高维度的仿射变换映射为低维度的平移),这样才能更好的理解这个世界的本质。