机器学习线性模型：一元线性回归问题实现（matlab）

1. 机器学习（一）线性回归

给定数据集 D={( $x_1$, $y_1$),( $x_2$, $y_2$),…,( $x_m$, $y_m$)},其中 $x_i = (x_{i1};x{_i2};...;x_{id}),y_i \in R$。“线性回归”（linear regression）试图学的一个线性模型以尽可能地准确预测实值输出标记

当前我只考虑输入属性的数目为一个

对于下面的实现主要给出代码中体现计算的一些公式，在吴恩达老师的视频以及周志华老师的《机器学习》一书中很容易实现，而我后期机器学习基本公式推导、模型讲解以及相关的改进也是基于上述的资料。

1.1最小二乘法

线性回归试图学得
$f(x_i) = \omega x_i+b$
性能度量：均方误差
基于均方误差最小化来进行模型求解的方法称为“最小二乘法”
求得的参数 $\omega$和 $b$最优解的闭式解
$\omega = \frac{\sum_{i=1}^m y_i(x_i-x)}{\sum_{i=1}^m x_i^2-\frac1m(\sum_{i=1}^m x_i)^2}$
$b = \frac1m \sum_{i=1}^{m}(y_i-\omega x_i)$
具体的matlab代码实现：

function [coef_,intercept_]=Linearmodel_1D(X,y)
m = size(X,2);
average_x = sum(X)/m;
w_t = sum(y.*(X-average_x));
w_b = sum(X.^2)-(sum(X)).^2/m;
coef_ = w_t/w_b;
intercept_ = sum(y-coef_*X)/m;
y_predict = coef_*X+intercept_;
plot(X,y,'ro',X,y_predict,'b--');
legend('Training data','Linear regression');
end

1.2 梯度下降

梯度下降采用吴恩达老师课程讲解的内容，具体简单写一下一元线性回归的必备知识点：

• 假设函数： $h_{\theta}(x) = \theta_0+\theta_1 x$
• 参数： $\theta_0$, $\theta_1$
• 代价函数(Cost function):
  $J(\theta_0,\theta_1) = \frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^2$
• 目的： $minimize_{\theta_0,\theta_1} J(\theta_0,\theta_1)$

具体的代码实现：

clc;
clear;
data = load('test.txt');
X = data(:,1);
y = data(:,2);
[coef,intercep]=Linearmodel_1D(X,y)
figure;
plot(X,y,'r*');

% x加入一列，变成（25,2）
m = length(y);
X = [ones(m,1),data(:,1)];
% 初始化参数
theta = zeros(2,1);

% Gradient descent settings
iterate = 1000;
alpha = 0.01;
% 梯度下降，找到最佳参数
theta = gradientDescent(X,y,theta,alpha,iterate)

hold on;
% keep previous plot visible
plot(X(:,2),X*theta,'-');
legend('Training data','Linear regression of gradient descent');
hold off;

梯度下降函数的具体迭代公式如下：

$\theta_0 := \theta_0-\alpha \frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})$
$\theta_1 := \theta_1-\alpha \frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})$

function theta = gradientDescent(X,y,theta,alpha,num_iters)
m = length(y);
%样本数量
for iter = 1: num_iters
    H = X*theta;
    theta_sum = [0;0];
    %theta_0更新
    for i = 1:m
        theta_sum(1,1)=theta_sum(1,1)+(H(i)-y(i));
    end
    
    % theta_1 更新
    for i = 1:m
        theta_sum(2,1)=theta_sum(2,1)+(H(i)-y(i))*X(i,2);
    end
    
    theta = theta-(alpha*theta_sum)/m;
end
end

同时为了比较最下二乘法和梯度下降算法，绘制出两类算法对应的图像以及相应参数如下
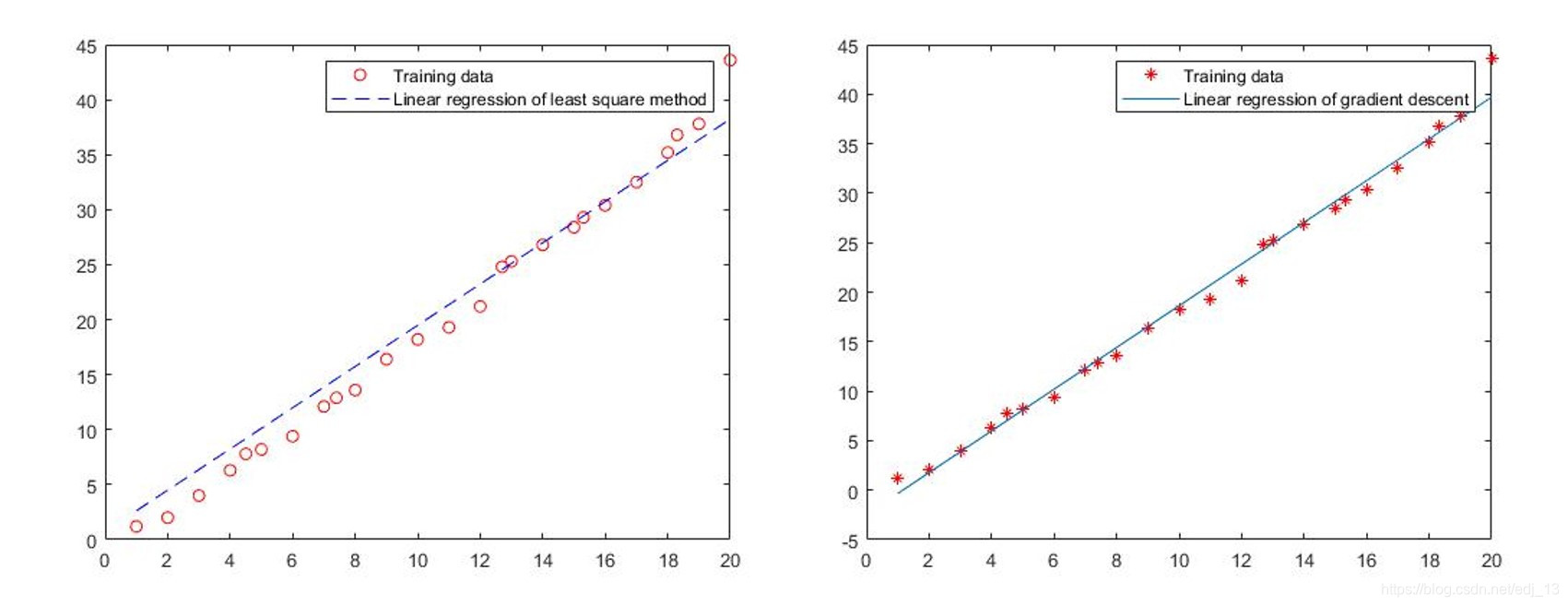最小二乘法 $\theta_0$=0.7463 $\theta_1$=1.8745
梯度下降法 $\theta_0$=-2.448 $\theta_1$=2.1077

1.3问题

1. 对于上述求得的假设函数应该如何选取？
2. 不同的单变量线性回归，不同方法的选取的标准是什么？

对于我这个机器新手来说，还需要进一步加深理解，如果有啥大神来了可以帮我解答一下，我会非常感谢的！！