树状数组（BIT）

树状数组入门（Binary Indexed Tree）

树状数组是一种利用数的二进制特征进行检索的树状结构。是一种高效地对一个数字的列表进行更新及求前缀和的数据结构。

• 树状数组
  在学习树状数组前，先看一下树状数组的结构：
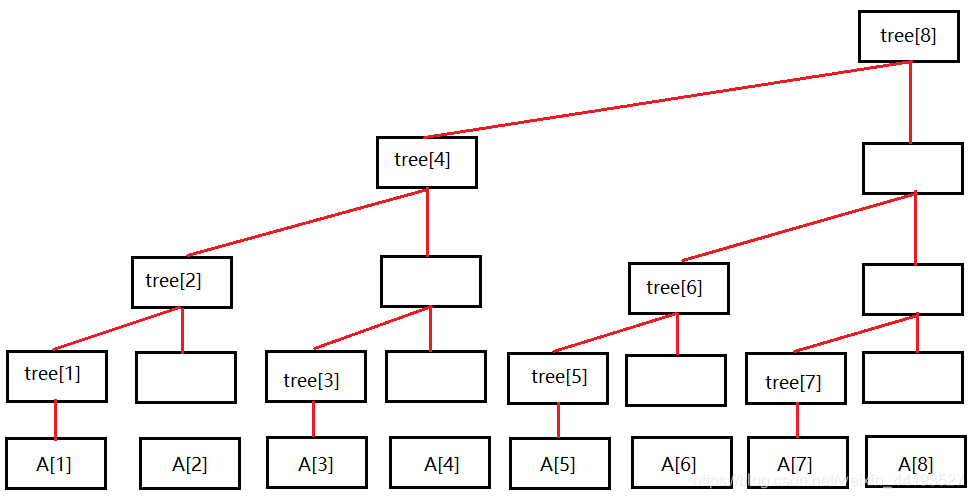  A[n] 数组是原数组
  tree[n] 数组就是树状数组，包含如下关系：

  tree[1] = A[1]　　　　　　　　　　　　tree[2] = A[1]+A[2]
  tree[3] = A[3]　　　　　　　　　　　　tree[4] = A[1]+A[2]+A[3]+A[4]
  tree[5] = A[5]　　　　　　　　　　　　tree[6] = A[5]+A[6]
  tree[7] = A[7]　　　　　　　　　　　　tree[8] = A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8]

  看完树状数组的结构之后你可能完全不知道这其中存在什么关系或是好奇为什么会有这样的结构，接下来我们就学习一下树状数组的知识。

• lowbit()操作
  在学习树状数组之前，先学习一下树状数组的前置知识—lowbit() 操作。
  
  这个lowbit() 操作实际上是用来取得一个十进制数用二进制表达时，最低位的 1 及其后面的零转化成十进制所对应的值。例如 (6)₁₀ 的二进制表达为 (1010)₂ ,那么 lowbit(6) 就等于 (10)₂ ，对应十进制就是 (2)₁₀ 。
  
  lowbit(x) = ((x) & (-x)) ,这个式子就完成了上述操作，其原理利用了计算机内部一个数的负数用其二进制补码表示。例如 x = (6)₁₀ 的二进制为 (1010)₂ ，它的补码就是 (0110)₂ ，所以 ((x) & (-x)) = (1010)₂ & (0110)₂ = (0010)₂ = (2)₁₀ 。

• 构造树状数组
  了解了lowbit() 操作之后，我们来看这个树状数组是如何构造出来的。
  
  这里我们令 m = lowbit(x) ，定义 tree[x] 为 A[x] 和 他前面 m 个数相加的结果。例如 lowbit(6) = 2 ,则 tree[6] = A[6] + A[5] 。通过这个定义，就不难理解文章一开始给出 tree[n] 数组的关系了。
  

  那么问题来了，前面说过，这个数据结构可以帮助我们快速高效地进行更新和求前缀和，那我们怎么才能应用这个树状数组呢？接下来我们就学习一下树状数组的区间求和和单点更新操作。
  

• 区间求和
  首先我们先看一个例子，求前六个数的和，即 sum(6) = A[1]+A[2]+…+A[6] 。
  结合文章前面给出的树状数组的关系，可以看出，sum(6) = tree[6] + tree[4] 可以快速求得前六个值的和。
  到这里有没有看出什么规律来呢。其实，(6)₁₀ 对应的二进制表示为 (1010)₂ ,
  首先 sum(6) = 0 + tree[6] ,
  然后对 (6)₁₀ 进行下面操作 6-lowbit(6) ,那么现在就是 6-2=4 ，sum(6) 再加上 tree[4] ，此时 sum(6) = 0 + tree[6] + tree[4] 。
  然后再进行上述操作 4-lowbit(4) = 0, 我们的数组 A[n] 是从 1 开始的，所以此时求和操作就结束了。
  所以最后的结果是 sum(6) = tree[6] + tree[4] 。
  
  从上面这个例子可以看出来，区间和是如何通过 树状数组 和 lowbit() 操作得到了，并且将复杂度降到了 O(log₂n) 。下面是代码实现。

  int sum(int x){
      int sum = 0;
      while(x>0){
          sum += tree[x];
          x -= lowbit(x);
      }
      return sum;
  }
  

  通过上面的介绍可以看出，所谓的求区间和实际上是求前缀和，并不像线段树一样，可以求任意区间的和，树状数组默认求和区间是 [1…x] 。当需要求任意区间的时候可以通过区间和相减的方法完成。
  相关线段树的内容可以看一下另一篇文章 线段树入门

• 单点更新
  说完了区间求和的问题，我们来说一下树状数组单点更新（这里的更新只涉及加上或减去某个值）的问题。
  
  通过介绍树状数组的构建，我们知道，树状数组中某个元素 tree[x] 是原数组中一系列包含 A[x] 及其前面 lowbit(x) 个数的和，所以 A[x] 的改变关系到了 tree[x] 和后面某些元素的值，所以，当我们更新原数组中的 A[x] 时，要同时更新 tree[x] 和与他相关的元素。例如改变 A[3] 的值，同时要更新 tree[3] 、tree[4]、 tree[8] 的值。
  
  那如何确定到底需要更新哪些元素呢。这里依旧使用到了 lowbit() 操作。还是以 A[3] 为例：
  首先更新 tree[3] ，
  然后 3 + lowbit(3) = 4 ，更新 tree[4] ，
  然后 4 + lowbit(4) = 8 ，更新 tree[8] ，
  重复进行，直到更新到 tree[n] 。
  下面是代码实现：

  void add(int x, int d){  //d是要加上或者减去的数
      while(x<=n){
          tree[x] += d;
          x += lowbit(x);
      }
  }
  

• 区间更新
  学过线段树的话，我们会知道还有一个操作叫区间更新，如果我们的操作是多次更新区间的值（区间内每个元素同时加上或减去某个值），使用树状数组的话，复杂度是很高的，远远超过了直接更新原数组的值。线段树的区间更新需要借助 lazy 标记。同样，一个序列的区间更新可以借助 差分数组 ，其时间复杂度远远低于直接更新。差分数组请见下一篇博客：差分数组。