Binary Search Tree 二叉搜索树
树形数据结构在实际应用中相当广泛,尤其是二叉树,二叉树具有鲜明的特点,一个节点具有一个数据域,两个指针域,分别指向左孩子和右孩子,如下图
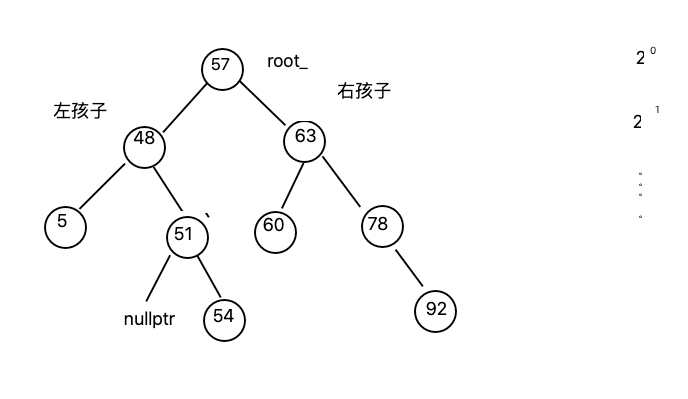
特点如下
- 若左子树不为空,则左子树上的所以值小于其根节点
- 若右子树不为空,则右子树上的所有值大于根节点
- 左右子树也满足二叉树的特点
- 左孩子小于父节点,父节点小于右孩子
每一层的节点个数以2的n次方增长,因此树的高度就是以2为logn 因此在查找元素时,时间复杂度为以2为底的logn
二叉树的节点类型
template<typename T,typename Comp=less<T>> class BSTree { public: private: struct Node { Node(T data=T()):data_(data),left_(nullptr),right_(nullptr){} T data_; // 数据域 Node *left_; // 左孩子指针 Node *right_; // 右孩子指针 }; Node *root_; // 指向BST树的根节点 Comp comp_; // 函数对象类型 (比较小于的函数对象) };
二叉树的插入理论
如果要插入的值为val
- 判断根节点root_节点是否为空 如果是插入根节点 结束
若根节点不为空,则拿val 和 节点里面的data进行比较, val>data 说明要往当前节点的右子树走,若 val<data 要往当前节点的左子树走 一直比较,直到找到某个节点的孩子节点为nullptr,然后将val 插入,同时定义一个指针指向父节点,更新父亲节点对应的地址域
// 非递归插入 void n_insert(const T &val) { if(root_==nullptr) { root_=new Node(val); return; } Node *cur=root_; Node *parent=nullptr; // 记录父节点 方便插入之后更新父节点对应的地址域 while(cur!=nullptr) { if(comp_(cur->data_,val)) // val 比当前节点大 往右子树走 { parent=cur; cur=cur->right_; } else if(!comp_(cur->data_,val)) // val 比当前值小,往左子树走 { parent=cur; cur=cur->left_; } else // 元素相同 什么都不干 { return; } } // 插入节点并且更新父节点对应的地址域 if(comp_(parent->data_,val)) { parent->right_=new Node(val); } else { parent->left_=new Node(val); } }
// 递归插入用户接口 void insert(const T &val) { root_=insert(root_,val); } private: // 递归插入 Node * insert(Node *s,const T &val) { if(s==nullptr) // 如果没有根节点 创建根节点 或找到nullptr 叶子节点插入 { return new Node(val); } if(comp_(s->data_,val)) // 比节点值大 往右枝走 { s->right_=insert(s->right_,val); // 给父节点返回当前节点的地址 } else if(comp_(val,s->data_)) // 比节点值小, 往左枝走 { s->left_=insert(s->left_,val); // 给父节点返回当前前节点的地址 } return s; // 返回地址 }
二叉树删除理论
扫描二维码关注公众号,回复: 9360886 查看本文章
如果要删除的的值为 val
- 删除分为两种情况 a: 要删除的值只有一个孩子 或者是叶子节点,没有孩子 b: 要删除的值具有左右孩子
- 当为b 的情况是 删除方法为 找到该结点的前驱节点或者后继节点 ,将前驱或者后继节点的值覆盖要删除的节点的值,然后删除前驱或者后继 ,而前驱节点或者后继节点符合情况a (前驱的意思就是 当前节点的左子树上最大的值,后继是当前节点右子树上最小的值)
- 当为情况a的时候 , 找到要删除的节点 ,若该节点有个孩子,删除后要将该孩子节点挂到父节点相对应的地址域中,若没有孩子,要将父节点的对应的地址域赋值为nullptr
考虑特殊情况 删除的为根节点 要判断一下 若删除的节点父节点为nullptr,说明为root节点,此时要将更新一下root 节点
// 非递归删除 void n_remove(const T &val) { if(root_==nullptr) { return; } Node *cur=root_; Node *parent=nullptr; while(cur!=nullptr) { if(comp_(cur->data_,val)) { parent=cur; cur=cur->right_; } else if(comp_(val,cur->data_)) { parent=cur; cur=cur->left_; } else { break; //找到了 } } if(cur==nullptr) { return; //没找到 } if(cur->left_!=nullptr&&cur->right_!=nullptr) // 有左右孩子的情况 { Node *pre=cur->left_; parent=cur; while(pre->right_!=nullptr) { parent=pre; pre=pre->right_; } cur->data_=pre->data_; cur=pre; // 统一处理处理成只有一个节点或者是叶子节点 } Node *child=cur->left_; if(child==nullptr) // 没有左右孩子的情况 { child=cur->right_; } if(parent==nullptr) { root_=child; } else { if(parent->left_==cur) { parent->left_=child; } else { parent->right_=child; } } delete cur; }
// 递归删除用户接口 void remove(const T &val) { root_=remove(root_,val); } private: // 递归删除 Node * remove(Node *s,const T &val) { if(s==nullptr) // 如果没有找到 返回nullptr { return nullptr; } if(comp_(s->data_,val)) // 比节点值大 往右枝走 { s->right_=remove(s->right_,val); } else if(comp_(val,s->data_)) // 比节点值小 ,往左枝走 { s->left_=remove(s->left_,val); } else // 找到了 { if(s->left_!=nullptr&&s->right_!=nullptr) // 该结点具有左孩子和右孩子 把该结点的前驱节点的值 覆盖当前节点 然后删除前驱节点 { Node *pre=s->left_; while(pre->right_!=nullptr) { pre=pre->right_; } s->data_=pre->data_; s->left_=remove(s->left_,pre->data_); // 将左子枝 和前驱值再次递归 删除 } else // 该结点 为叶子节点或者只有一个孩子节点 { if(s->left_!=nullptr) // 要删除的左子树上还有节点 { Node *tmp=s->left_; delete s; return tmp; } else if(s->right_!=nullptr) // 右子树上还有节点 { Node *tmp=s->right_; delete s; return tmp; } else // 叶子节点 { delete s; return nullptr; } } } return s; }
前序遍历VLR
- 遍历二叉树的第一种方法就是前序遍历 前序遍历的要求是先访问当前节点的值,然后访问左孩子最后访问右孩子
- 这访问方式是要基于每一个节点,
- 例如 先访问根节点的值,然后访问左子树 当到达左子树时,又要遵循VLR这个方式,即访问当前元素的值,又进入左子树 只有深度遍历完 才开始访问右节点 看具体代码
- 在访问的过程中要用的栈结构将每个节点进行记录 根据栈的先进后出,虽然是VLR 入栈 的时候要将右子树先入,这样就是后访问
// 非递归前序遍历查找VLR void n_preOrder() { if(root_==nullptr) { return; } cout<<"非递归前序遍历:"; stack<Node *>s; s.push(root_); // 将根节点先入栈 while(!s.empty()) { Node *top=s.top(); // 获取栈顶元素 cout<<top->data_<<" "; // V s.pop(); // 出栈 if( top->right_!=nullptr) // 右孩子入栈 后访问R { s.push(top->right_); } if(top->left_!=nullptr) // 左孩子入栈 先访问 L { s.push(top->left_); } } cout<<endl; }
// 递归前序遍历用户接口VLR void preOrder() { cout<<"前序遍历: "; preOrder(root_); cout<<endl; } private: void preOrder(Node *s) { if(s!=nullptr) { cout<<s->data_<<" "; // V preOrder(s->left_); // L preOrder(s->right_); // R } }
中序遍历LVR
- 中序遍历和前序遍历的区别就是对元素访问方式发生改变,每当到一个节点的时候,先访问左子树,再访问节点的值,最后访问右节点
- 这样形成的访问会是一个递增形式
- 同样需要一个栈结构,对节点进行存储
// 非递归中序遍历LRV void n_inOrder() { if(root_==nullptr) { return; } cout<<"非递归中序遍历: "; stack<Node *>s; Node *cur=root_; while(!s.empty()||cur!=nullptr) { if(cur!=nullptr) // 先访问左子树 L { s.push(cur); cur=cur->left_; } else { Node *top=s.top(); cout<<top->data_<<" "; // V s.pop(); cur=top->right_; // R } } cout<<endl; }
void inOrder(Node *s) { if(s!=nullptr) { inOrder(s->left_); // L cout<<s->data_<<" "; // V inOrder(s->right_); // R } }
后序遍历 LRV
后序遍历理论
- 后序遍历的非递归 先访问左子树,,在访问右子树 最后访问节点的值,但是不方便记录节点 因为是深度遍历已经下去,无法存放父节点 因此要换一种思想 VRL 类似于前序遍历然后逆序输出
- 用到两个栈结构 第一个栈对节点深度遍历进行存储,第二个负责存储访问的元素值,,方便最后逆序输出
// 非递归后序遍历LRV 方法:LRV 不易保存V 采用VRL方式 然后倒叙输出 用两个栈 void n_postOrder() { if(root_==nullptr) { return; } cout<<"非递归后序遍历: "; stack<Node *> s,p; s.push(root_); while(!s.empty()) { Node *top=s.top(); p.push(top); // V 将s栈顶元素push 到P这个栈里 s.pop(); if(top->left_!=nullptr) // 先入栈的后访问 左孩子入栈L { s.push(top->left_); } if(top->right_!=nullptr) // 右孩子入栈 先访问 符合VRL { s.push(top->right_); } } while(!p.empty()) // 最后将P 这个栈的元素输出,根据栈的先进后出 刚好到达逆序效果 { Node *top=p.top(); cout<<top->data_<<" "; p.pop(); } cout<<endl; }
// 后序遍历 void postOrder(Node *s) { if(s!=nullptr) { postOrder(s->left_); // L postOrder(s->right_); // R cout<<s->data_<<" "; // V } }
层序遍历
层序遍历的理论
- 层序遍历,即先访问当前节点的值,然后访问左孩子的值,访问右孩子的值,
- 访问结构,根元素在树中存储的结构一样
这个就是广度优先,利用队列 先进先出
// 非递归的层序遍历,广度遍历 ,借用队列 void n_tierOrder() { if(root_==nullptr) { return; } cout<<"非递归层序遍历: "; queue<Node *>q; q.push(root_); while(!q.empty()) { Node *f=q.front(); cout<<f->data_<<" "; q.pop(); if(f->left_!=nullptr) { q.push(f->left_); } if(f->right_!=nullptr) { q.push(f->right_); } } cout<<endl; }
递归的层序遍历还需要知道树的高度 树的高度求解理论知识
- 先深度遍历到叶子节点上,在回溯的过程中,记录树的高度
- 深度遍历到左右孩子的叶子节点,比较左右子树的高度,高的+但前一个节点 返回给上一个节点
// 递归求二叉树层数 int high() { return high(root_); } private: // 求二叉树高度 int high(Node *s) { if(s==nullptr) // 遍历的叶子节点则返回空 { return 0; } int left=high(s->left_); // 左子树往下递归 int right=high(s->right_); // 然后右子树往下遍历 return left>right?left+1:right+1; // 往上回溯 下面的层数+本层的一个往上回溯 }
// 层序遍历 void leveOrder() { cout<<"层序遍历 : "; int i,h=high(); for(i=0;i<h;i++) { leveOrder(root_,i); } cout<<endl; } private: //层序遍历 void leveOrder(Node* s,int i) { if(s==nullptr) { return; } if(i==0) { cout<<s->data_<<" "; return; } leveOrder(s->left_,i-1); leveOrder(s->right_,i-1); }
源码
#include<iostream> #include<stdlib.h> #include<string.h> #include<functional> #include<string> #include<unistd.h> #include<stack> #include<queue> using namespace std; template<typename T,typename Comp=less<T>> class BSTres { public: BSTres():root_(nullptr){} ~BSTres() { } // 非递归插入 void n_insert(const T &val) { if(root_==nullptr) { root_=new Node(val); return; } Node *cur=root_; Node *parent=nullptr; // 记录父节点 方便插入之后更新父节点对应的地址域 while(cur!=nullptr) { if(comp_(cur->data_,val)) // val 比当前节点大 往右子树走 { parent=cur; cur=cur->right_; } else if(!comp_(cur->data_,val)) // val 比当前值小,往左子树走 { parent=cur; cur=cur->left_; } else // 元素相同 什么都不干 { return; } } // 插入节点并且更新父节点对应的地址域 if(comp_(parent->data_,val)) { parent->right_=new Node(val); } else { parent->left_=new Node(val); } } // 非递归删除 void n_remove(const T &val) { if(root_==nullptr) { return; } Node *cur=root_; Node *parent=nullptr; while(cur!=nullptr) { if(comp_(cur->data_,val)) { parent=cur; cur=cur->right_; } else if(comp_(val,cur->data_)) { parent=cur; cur=cur->left_; } else { break; //找到了 } } if(cur==nullptr) { return; //没找到 } if(cur->left_!=nullptr&&cur->right_!=nullptr) // 有左右孩子的情况 { Node *pre=cur->left_; parent=cur; while(pre->right_!=nullptr) { parent=pre; pre=pre->right_; } cur->data_=pre->data_; cur=pre; // 统一处理处理成只有一个节点或者是叶子节点 } Node *child=cur->left_; if(child==nullptr) // 没有左右孩子的情况 { child=cur->right_; } if(parent==nullptr) { root_=child; } else { if(parent->left_==cur) { parent->left_=child; } else { parent->right_=child; } } delete cur; } // 非递归查找 bool n_find(const T &val) { while(root_!=nullptr) { if(comp_(root_->data_,val)) { root_=root_->right_; } else if(comp_(val,root_->data_)) { root_=root_->left_; } else { return true; } } return false; } // 非递归前序遍历查找VLR void n_preOrder() { if(root_==nullptr) { return; } cout<<"非递归前序遍历:"; stack<Node *>s; s.push(root_); // 将根节点先入栈 while(!s.empty()) { Node *top=s.top(); // 获取栈顶元素 cout<<top->data_<<" "; // V s.pop(); // 出栈 if( top->right_!=nullptr) // 右孩子入栈 后访问R { s.push(top->right_); } if(top->left_!=nullptr) // 左孩子入栈 先访问 L { s.push(top->left_); } } cout<<endl; } // 非递归中序遍历LRV void n_inOrder() { if(root_==nullptr) { return; } cout<<"非递归中序遍历: "; stack<Node *>s; Node *cur=root_; while(!s.empty()||cur!=nullptr) { if(cur!=nullptr) // 先访问左子树 L { s.push(cur); cur=cur->left_; } else { Node *top=s.top(); cout<<top->data_<<" "; // V s.pop(); cur=top->right_; // R } } cout<<endl; } // 非递归后序遍历LRV 方法:LRV 不易保存V 采用VRL方式 然后倒叙输出 用两个栈 void n_postOrder() { if(root_==nullptr) { return; } cout<<"非递归后序遍历: "; stack<Node *> s,p; s.push(root_); while(!s.empty()) { Node *top=s.top(); p.push(top); // V 将s栈顶元素push 到P这个栈里 s.pop(); if(top->left_!=nullptr) // 先入栈的后访问 左孩子入栈L { s.push(top->left_); } if(top->right_!=nullptr) // 右孩子入栈 先访问 符合VRL { s.push(top->right_); } } while(!p.empty()) // 最后将P 这个栈的元素输出,根据栈的先进后出 刚好到达逆序效果 { Node *top=p.top(); cout<<top->data_<<" "; p.pop(); } cout<<endl; } // 非递归的层序遍历,广度遍历 ,借用队列 void n_tierOrder() { if(root_==nullptr) { return; } cout<<"非递归层序遍历: "; queue<Node *>q; q.push(root_); while(!q.empty()) { Node *f=q.front(); cout<<f->data_<<" "; q.pop(); if(f->left_!=nullptr) { q.push(f->left_); } if(f->right_!=nullptr) { q.push(f->right_); } } cout<<endl; } private: struct Node { Node(T data=T()):data_(data),left_(nullptr),right_(nullptr){} T data_; // 数据域 Node *left_; // 左孩子指针 Node *right_; // 右孩子指针 }; Node *root_; // 指向BST树的根节点 Comp comp_; }; int main() { BSTres<int> bst; int arr[]={58,24,67,0,34,62,69,5,41,64,78}; for(int v:arr) { bst.n_insert(v); } bst.n_insert(12); bst.n_remove(12); bst.n_preOrder(); bst.n_inOrder(); bst.n_postOrder(); bst.n_tierOrder(); return 0; }
// 递归
#include<iostream> #include<stdlib.h> #include<string.h> #include<string> #include<unistd.h> #include<vector> #include<queue> using namespace std; template <typename T,typename Comp=less<T>> class BSTree { public: BSTree(Comp comp=Comp()):root_(nullptr),comp_(comp){} // 析构函数 利用非递归的层序遍历 ~BSTree() { if(root_!=nullptr) { queue<Node *>s; s.push(root_); while(!s.empty()) { Node *front=s.front(); s.pop(); if(front->left_!=nullptr) { s.push(front->left_); } if(front->right_!=nullptr) { s.push(front->right_); } delete front; } } } // 递归插入用户接口 void insert(const T &val) { root_=insert(root_,val); } // 递归查找用户接口 bool find(const T &val) { return nullptr!=find(root_,val); } // 递归删除用户接口 void remove(const T &val) { root_=remove(root_,val); } // 递归前序遍历用户接口VLR void preOrder() { cout<<"前序遍历: "; preOrder(root_); cout<<endl; } // 中序遍历LVR void inOrder() { cout<<"中序遍历 :"; inOrder(root_); cout<<endl; } // 后序遍历 void postOrder() { cout<<"后序遍历 :"; postOrder(root_); cout<<endl; } // 层序遍历 void leveOrder() { cout<<"层序遍历 : "; int i,h=high(); for(i=0;i<h;i++) { leveOrder(root_,i); } cout<<endl; } // 递归求二叉树层数 int high() { return high(root_); } // 递归求二叉树节点个数 int nodenum() { return nodenum(root_); } private: struct Node { Node(T data=T()):data_(data),left_(nullptr),right_(nullptr){} T data_; Node *left_; Node *right_; }; // 递归插入 Node * insert(Node *s,const T &val) { if(s==nullptr) // 如果没有根节点 创建根节点 或找到nullptr 叶子节点插入 { return new Node(val); } if(comp_(s->data_,val)) // 比节点值大 往右枝走 { s->right_=insert(s->right_,val); // 给父节点返回当前节点的地址 } else if(comp_(val,s->data_)) // 比节点值小, 往左枝走 { s->left_=insert(s->left_,val); // 给父节点返回当前前节点的地址 } return s; // 返回地址 } Node * find(Node *s,const T &val) { if(s==nullptr) // 如果为nullptr 表示没有找到 { return nullptr; } if(s->data_==val) // 找到了 返回地址 { return s; } else if(comp_(s->data_,val)) // 如果比节点值大 往右枝走 { return find(s->right_,val); } else { return find(s->left_,val); // 如果比节点值小 往左枝走 } } // 递归删除 Node * remove(Node *s,const T &val) { if(s==nullptr) // 如果没有找到 返回nullptr { return nullptr; } if(comp_(s->data_,val)) // 比节点值大 往右枝走 { s->right_=remove(s->right_,val); } else if(comp_(val,s->data_)) // 比节点值小 ,往左枝走 { s->left_=remove(s->left_,val); } else // 找到了 { if(s->left_!=nullptr&&s->right_!=nullptr) // 该结点具有左孩子和右孩子 把该结点的前驱节点的值 覆盖当前节点 然后删除前驱节点 { Node *pre=s->left_; while(pre->right_!=nullptr) { pre=pre->right_; } s->data_=pre->data_; s->left_=remove(s->left_,pre->data_); // 将左子枝 和前驱值再次递归 删除 } else // 该结点 为叶子节点或者只有一个孩子节点 { if(s->left_!=nullptr) // 要删除的左子树上还有节点 { Node *tmp=s->left_; delete s; return tmp; } else if(s->right_!=nullptr) // 右子树上还有节点 { Node *tmp=s->right_; delete s; return tmp; } else // 叶子节点 { delete s; return nullptr; } } } return s; } // 前序遍历 void preOrder(Node *s) { if(s!=nullptr) { cout<<s->data_<<" "; // V preOrder(s->left_); // L preOrder(s->right_); // R } } // 中序遍历 void inOrder(Node *s) { if(s!=nullptr) { inOrder(s->left_); // L cout<<s->data_<<" "; // V inOrder(s->right_); // R } } // 后序遍历 void postOrder(Node *s) { if(s!=nullptr) { postOrder(s->left_); // L postOrder(s->right_); // R cout<<s->data_<<" "; // V } } //层序遍历 void leveOrder(Node* s,int i) { if(s==nullptr) { return; } if(i==0) { cout<<s->data_<<" "; return; } leveOrder(s->left_,i-1); leveOrder(s->right_,i-1); } // 求二叉树高度 int high(Node *s) { if(s==nullptr) // 遍历的叶子节点则返回空 { return 0; } int left=high(s->left_); // 左子树往下递归 int right=high(s->right_); // 然后右子树往下遍历 return left>right?left+1:right+1; // 往上回溯 下面的层数+本层的一个往上回溯 } // 求节点个数 int nodenum(Node *s) { if(s==nullptr) // 遍历到叶子节点返回0 { return 0; } int left=nodenum(s->left_); int right=nodenum(s->right_); return left+right+1; } Comp comp_; Node *root_; }; int main() { BSTree<int> bst; int arr[]={58,24,67,0,34,62,69,5,41,64,78}; for(int v:arr) { bst.insert(v); } bst.inOrder(); bst.leveOrder(); cout<<bst.high()<<" "<<bst.nodenum()<<endl; return 0; }