二叉查找树（BST)、平衡二叉树(AVL树)

二叉查找树(BST)

　　特殊的二叉树，又称为排序二叉树、二叉搜索树、二叉排序树。

　　二叉查找树实际上是数据域有序的二叉树，即对树上的每个结点，都满足其左子树上所有结点的数据域均小于或等于根结点的数据域，右子树上所有结点的数据域均大于根结点的数据域。如下图所示：

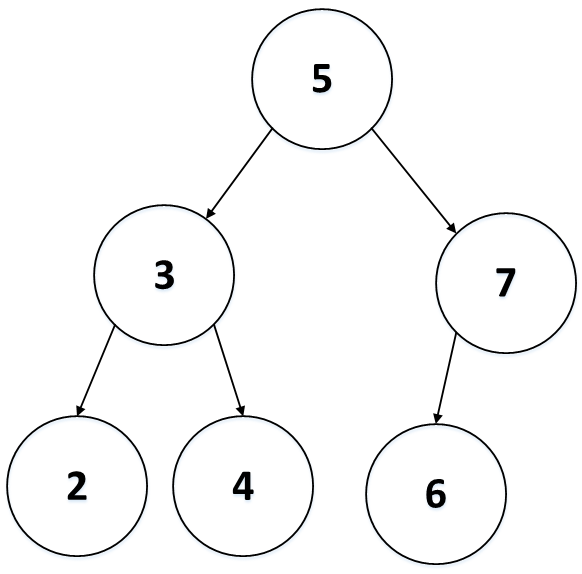
二叉查找树通常包含查找、插入、建树和删除操作。

二叉查找树的创建

对于一棵二叉查找树，其创建与二叉树的创建很类似，略有不同的是，二叉查找树，为了保证整棵树都关于根结点的大小呈左小右大的特征，在创建时，需要根据当前结点的大小来判断插入位置，给出如下代码：

template<typename T>
void  BSTree<T>::createBSTreeByFile(ifstream &f){
    T e;
    queue<BSNode<T>*> q;

    while(!f.eof()){
        InputFromFile(f, e);
        Insert(root, e);
    }
}

template<typename T>
void BSTree<T>::Insert(BSNode<T>* &t, T x){//得用指针的引用，不然传参时由于形参实例化，并不能成功创建二叉树

    if(t==NULL){
        t = new BSNode<T>;
        t->data = x;
        t->lchild = t->rchild = NULL;
        return;
    }

    if(x<=t->data){
        Insert(t->lchild, x);
    }
    else{
        Insert(t->rchild, x);
    }
}

二叉查找树的查找

二叉查找树的查找有递归和非递归两种，对于递归方式，其递归边界为树的终止结点，非递归方式则采取对树中所有结点采取BFS或者DFS进行遍历的方式。

对于非递归方式，给出采取DFS的遍历方式，在这种方式中，通常采用入栈的方式，来访问每个结点，而根据访问的先后顺序，又分为，前序、中序和后序三种遍历方式。以前序遍历为例，通常以根、左、右的顺序访问遍历每个结点，而中序遍历方式，则以左、根、右的顺序遍历，后序则以左右根的顺序来访问。下面给出三种遍历方式的代码：前序遍历：

 1 template<typename T>
 2 void BSTree<T>::PreOrderTraverse(void(*visit)(BSNode<T>&))const{
 3     stack<BSNode<T>*> s;
 4     BSNode<T> *t = root;
 5     while(NULL!=t || !s.empty()){
 6         if(NULL!=t){
 7             s.push(t);
 8             visit(*t);
 9             t = t->lchild;
10         }
11         else{
12             t = s.top();
13             s.pop();
14             t = t->rchild;
15         }
16     }
17     cout<<endl;
18 }

中序遍历：

 1 template<typename T>
 2 void BSTree<T>::InOrderTraverse(void(*visit)(BSNode<T>&))const{
 3     stack<BSNode<T>*> s;
 4     BSNode<T> *q;
 5 
 6     q = root;
 7 
 8     while(!s.empty()||q!=NULL){
 9         if(q!=NULL){
10             s.push(q);
11             q = q->lchild;
12         }
13         else{
14             q = s.top();
15             s.pop();
16             visit(*q);
17             q = q->rchild;
18         }
19     }
20     cout<<endl;
21 }

后序遍历，对于后序遍历，直接采用入栈的方式进行访问，是不行的，因为根结点被访问两次，无法保证你在弹栈后，对该结点如何操作，因此，需要另设置一个flag参数，来指明该节点是否左右子树都访问过，代码如下，我这里是令定义一个结构体，来实现：

/*结构体部分*/
enum Tags{Left, Right};

template<typename T>struct StackElem
{
    BSNode<T> *p;
    Tags flag;
};

/*后序遍历代码部分*/
template<typename T>
void BSTree<T>::PostOrderTraverse(void(*visit)(BSNode<T>&))const{
    StackElem<T> se;
    stack<StackElem<T> > s;

    BSNode<T> *t;
    t = root;

    if(t==NULL){
        return;
    }
    while(t!=NULL||!s.empty()){
        while(t!=NULL){
            se.flag = Left;
            se.p = t;
            s.push(se);
            t = t->lchild;
        }
        se = s.top();
        s.pop();
        t = se.p;
        if(se.flag==Left){
            se.flag = Right;
            s.push(se);
            t = t->rchild;
        }
        else{
            visit(*t);
            t = NULL;
        }
    }
}

以下是递归实现部分，递归实现，则是以二叉树边界为递归边界，前面已经说过了，其余逻辑与非递归一致，因为递归的过程，可以看作是一个入栈和弹栈的过程，即，在未到达边界时，通过递归，来访问下一个结点，例如左结点，当触及边界，则访问该结点，由于每次递归状态都被计算机保存，因此，在访问一个结点以后，返回上一个结点的状态，会依次访问上去。

递归前序遍历：

 1 template<typename T>
 2 void BSTree<T>::PreTraverse(BSNode<T> *t, void(*visit)(BSNode<T>&))const{
 3     if(t==NULL){
 4         return;
 5     }
 6     else{
 7         visit(*t);
 8         PreTraverse(t->lchild, visit);
 9         PreTraverse(t->rchild, visit);
10     }
11 }

递归中序遍历：

 1 template<typename T>
 2 void BSTree<T>::InTraverse(BSNode<T> *t, void(*visit)(BSNode<T>&))const{
 3     if(t==NULL){
 4         return;
 5     }
 6     else{
 7         InTraverse(t->lchild, visit);
 8         visit(*t);
 9         InTraverse(t->rchild, visit);
10     }
11 }

递归后序遍历：

1 template<typename T>
2 void BSTree<T>::PostTraverse(BSNode<T> *t, void(*visit)(BSNode<T>&))const{
3     if(t!=NULL){
4         PostTraverse(t->lchild, visit);
5         PostTraverse(t->rchild, visit);
6         visit(*t);
7     }
8 }

平衡二叉树（AVL树）

　　平衡二叉树是由前苏联的两位数学家G.M.Adelse-Velskil和E.M.Landis提出，因此一般也称作AVL树，AVL树本质还是一棵二叉查找树，只是在其基础上增加了“平衡”的要求。所谓平衡是指，对AVL树的任意结点来说，其左子树与右子树的高度之差的绝对值不超过1，其中左子树与右子树的高度因子之差称为平衡因子。

　　如下所示，就是一棵由{1，2，3，4，5，7，8}构建的AVL树：

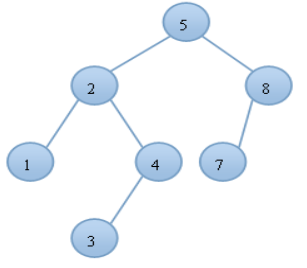
AVL树的创建

　　只要能随时保证每个结点平衡因子的绝对值不超过1，AVL的高度就始终能保持O(logn)级别，由于需要对每个结点都得到平衡因子，因此需要在树的结构中加入一个变量height来记录以当前结点为根结点的子树的高度：