伸展树（Splay）学习笔记

其他 2021-01-30 10:23:40 阅读次数: 0

简介

Splay是二叉搜索树的一种，也是平衡树的一种。其复杂度低的原因在于每次查找一个节点的时候，树都会重构使得深度降低，然后以后再访问周围的节点就会很快，不容易被卡。

既然是二叉搜索树，所以其每个节点最多只有2个子节点，且左儿子节点的值一定比它小，右儿子节点的值一定比它大。

例如：

节点结构

#define ls(x) T[x].ch[0]
#define rs(x) T[x].ch[1]
#define fa(x) T[x].fa
#define root T[0].ch[1]
struct node {
    
    
	int fa;		//父节点
	int ch[2];	//0代表左儿子，1代表右儿子
	int val;	//权值
	int rec;	//这个权值的节点出现的次数
	int size;	//子节点的数量（包含这个点）
};

基本操作

ident

获取一个节点x是它父亲节点的哪个儿子

int ident(int x) {
    
    
	return T[fa(x)].ch[0] == x ? 0 : 1;
}

update

更新一个节点x的值

void update(int x) {
    
    
	T[x].size = T[ls(x)].size + T[rs(x)].size + T[x].rec;
}

rotate

把一个节点x和它的父亲节点交换位置。

假设有树：

把X和Y互换位置后：

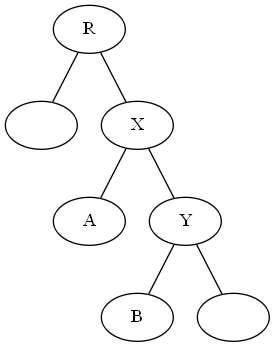
也可以描述为：

  • B成为Y的哪个儿子与X是Y的哪个儿子是一样的
  • Y成为X的哪个儿子与X是Y的哪个儿子是相反的
  • X成为R的哪个儿子与Y是R的哪个儿子是一样的
void connect(int x, int fa, int how) {
    
    
    T[fa].ch[how] = x;
    T[x].fa = fa;
}
void rotate(int x) {
    
    
    int Y = fa(x), R = fa(Y);
    int Yson = ident(x), Rson = ident(Y);
    connect(T[x].ch[Yson ^ 1], Y, Yson);
    connect(Y, x, Yson ^ 1);
    connect(x, R, Rson);
    update(Y);
    update(x);
}

splay

把一个节点x搬到to位置

为了方便操作，先把to赋值为to的父亲节点

to = fa(to);
int y = fa(x);

这时要分三种情况：

  1. to是x的父亲节点

    此时直接把x旋转上去即可

    if (T[y].fa == to) rotate(x);

  2. x和x的父亲的父亲在一条直线上

    此时应先把Y旋转上去，再把X旋转上去。（这里存疑，为啥直接旋转两次x就会T呢）

    2020/10/25答疑，因为连续旋转两次x会形成直链，而直链是搜索树退化的关键原因。先旋转y再旋转x就能有效地避免直链

    if (ident(x) == ident(y)) rotate(y), rotate(x);

  3. x和它父亲的父亲不在一条直线上

    直接旋转两次x

    rotate(x), rotate(x);

void splay(int x, int to) {
    
    
    to = fa(to);
    while (fa(x) != to) {
    
    
        int y = fa(x);
        if (T[y].fa == to)
            rotate(x);
        else if (ident(x) == ident(y))
            rotate(y), rotate(x);
        else
            rotate(x), rotate(x);
    }
}

newnode

新建节点：

int newnode(int v, int f) {
    
    
    T[++tot].fa = f;
    T[tot].rec = T[tot].size = 1;
    T[tot].val = v;
    return tot;
}

Insert

插入节点：

根据二叉搜索树的性质，找到节点要插入的位置，然后把它旋转到根节点的位置。

void Insert(int x) {
    
    
    int now = root;
    if (root == 0) {
    
     newnode(x, 0); root = tot; }
    else {
    
    
        while (1) {
    
    
            T[now].size++;
            if (T[now].val == x) {
    
    
                T[now].rec++;
                splay(now, root);
                return;
            }
            int nxt = x < T[now].val ? 0 : 1;
            if (!T[now].ch[nxt]) {
    
    
                int p = newnode(x, now);
                T[now].ch[nxt] = p;
                splay(p, root);
                return;
            }
            now = T[now].ch[nxt];
        }
    }
}

find

找到值为x的节点

根据二叉搜索树的性质进行查找，很简单，不赘述。

值得注意的是，在查找完成后，此节点将被旋转到根节点的位置。

int find(int x) {
    
    
    int now = root;
    while (1) {
    
    
        if (!now) return 0;
        if (T[now].val == x) {
    
    
            splay(now, root);
            return now;
        }
        int nxt = x < T[now].val ? 0 : 1;
        now = T[now].ch[nxt];
    }
}

delete

删除节点

当查找到节点x的时候，他已经被旋转到根节点了，所以此时我们不需关心他的父亲节点的情况。

那么有以下四种情况：

1.此节点的出现次数大于1

直接把出现次数和子树大小-1即可。

2.此节点没有左右儿子

此节点为根，且没有子节点，那么删除后就成了一颗空树。

3.此节点没有左儿子

直接把右儿子设置为根节点

之所以不考虑只有右儿子的情况是因为第4种情况会把左儿子中的值最大的节点设置为根节点，所以有没有右儿子都一样。

4.既有左儿子，又有右儿子

在左儿子里找到值最大的节点，设置成根节点。

void delet(int x) {
    
    
    int pos = find(x);
    if (!pos) return;
    if (T[pos].rec > 1) {
    
    
        T[pos].rec--, T[pos].size--;
        return;
    } else {
    
    
        if (!T[pos].ch[0] && !T[pos].ch[1]) {
    
    
            root = 0;
            return;
        } else if (!T[pos].ch[0]) {
    
    
            root = T[pos].ch[1];
            T[root].fa = 0;
            return;
        } else {
    
    
            int left = T[pos].ch[0];
            while (T[left].ch[1]) left = T[left].ch[1];
            splay(left, T[pos].ch[0]);
            connect(T[pos].ch[1], left, 1);
            connect(left, 0, 1);  //
            update(left);
        }
    }
}

rank

找到值为x的节点的排名

排名也等于左儿子子树的大小+1

int rak(int x) {
    
    
    // int now = root, ans = 0;
    // while (1) {
    
    
    //     if (T[now].val == x) return ans + T[T[now].ch[0]].size + 1;
    //     int nxt = x < T[now].val ? 0 : 1;
    //     if (nxt == 1) ans = ans + T[T[now].ch[0]].size + T[now].rec;
    //     now = T[now].ch[nxt];
    // }
	return T[ls(find(x))].size + 1;
}

arand

查询排名为x的值

用tem_num记录该节点以及左子树的节点数量，如果左子树的数量<x<tem_num，那么当前节点的权值就是答案。否则就根据二叉搜索树的性质继续搜索。

int arank(int x) {
    
    
    int now = root;
    while (1) {
    
    
        int tem_num = T[now].size - T[T[now].ch[1]].size;
        if (T[T[now].ch[0]].size < x && x <= tem_num) {
    
    
            splay(now, root);
            return T[now].val;
        }
        if (x < tem_num)
            now = T[now].ch[0];
        else
            now = T[now].ch[1], x -= tem_num;
    }
}

lower

求x的前驱，即小于x的最大值

编译一遍即可。

int lower(int x) {
    
    
    int now = root, ans = -INF;
    while (now) {
    
    
        if (T[now].val < x) ans = max(ans, T[now].val);
        int nxt = x <= T[now].val ? 0 : 1;  //这里需要特别注意
        now = T[now].ch[nxt];
    }
    return ans;
}

upper

求x的后继，即大于x的最小值

同样是遍历一遍即可。

int upper(int x) {
    
    
    int now = root, ans = INF;
    while (now) {
    
    
        if (T[now].val > x) ans = min(ans, T[now].val);
        int nxt = x < T[now].val ? 0 : 1;
        now = T[now].ch[nxt];
    }
    return ans;
}

完整代码

#pragma GCC optimize(2)
#include <bits/stdc++.h>
#define m_p make_pair
#define p_i pair<int, int>
#define _for(i, a) for(register int i = 0, lennn = (a); i < lennn; ++i)
#define _rep(i, a, b) for(register int i = (a), lennn = (b); i <= lennn; ++i)
#define outval(a) cout << "Debuging...|" << #a << ": " << a << "\n"
#define mem(a, b) memset(a, b, sizeof(a))
#define mem0(a) memset(a, 0, sizeof(a))
#define fil(a, b) fill(a.begin(), a.end(), b);
#define scl(x) scanf("%lld", &x)
#define sc(x) scanf("%d", &x)
#define pf(x) printf("%d\n", x)
#define pfl(x) printf("%lld\n", x)
#define abs(x) ((x) > 0 ? (x) : -(x))
#define PI acos(-1)
#define lowbit(x) (x & (-x))
#define dg if(debug)
#define nl(i, n) (i == n - 1 ? "\n":" ")
using namespace std;
typedef long long LL;
// typedef __int128 LL;
typedef unsigned long long ULL;
const int maxn = 100005;
const int maxm = 1000005;
const int maxp = 30;
const int inf = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1000000007;
const double eps = 1e-8;
const double e = 2.718281828;
int debug = 0;

inline int read() {
    
    
	int x(0), f(1); char ch(getchar());
	while (ch<'0' || ch>'9') {
    
     if (ch == '-') f = -1; ch = getchar(); }
	while (ch >= '0'&&ch <= '9') {
    
     x = x * 10 + ch - '0'; ch = getchar(); }
	return x * f;
}
#define ls(x) T[x].ch[0]
#define rs(x) T[x].ch[1]
#define fa(x) T[x].fa
#define root T[0].ch[1]
struct node {
    
    
    int fa;		//父节点
	int ch[2];	//0代表左儿子，1代表右儿子
	int val;	//权值
	int rec;	//这个权值的节点出现的次数
	int size;	//子节点的数量（包含这个点）
} T[maxn];
int tot = 0, pointnum = 0;
void update(int x) {
    
     T[x].size = T[ls(x)].size + T[rs(x)].size + T[x].rec; }
int ident(int x) {
    
     return T[fa(x)].ch[0] == x ? 0 : 1; }
void connect(int x, int fa, int how) {
    
    
    T[fa].ch[how] = x;
    T[x].fa = fa;
}
void rotate(int x) {
    
    
    int Y = fa(x), R = fa(Y);
    int Yson = ident(x), Rson = ident(Y);
    connect(T[x].ch[Yson ^ 1], Y, Yson);
    connect(Y, x, Yson ^ 1);
    connect(x, R, Rson);
    update(Y);
    update(x);
}
void splay(int x, int to) {
    
    
    to = fa(to);
    while (fa(x) != to) {
    
    
        int y = fa(x);
        if (T[y].fa == to)
            rotate(x);
        else if (ident(x) == ident(y))
            rotate(y), rotate(x);
        else
            rotate(x), rotate(x);
    }
}
int newnode(int v, int f) {
    
    
    T[++tot].fa = f;
    T[tot].rec = T[tot].size = 1;
    T[tot].val = v;
    return tot;
}
void Insert(int x) {
    
    
    int now = root;
    if (root == 0) {
    
     newnode(x, 0); root = tot; }
    else {
    
    
        while (1) {
    
    
            T[now].size++;
            if (T[now].val == x) {
    
    
                T[now].rec++;
                splay(now, root);
                return;
            }
            int nxt = x < T[now].val ? 0 : 1;
            if (!T[now].ch[nxt]) {
    
    
                int p = newnode(x, now);
                T[now].ch[nxt] = p;
                splay(p, root);
                return;
            }
            now = T[now].ch[nxt];
        }
    }
}
int find(int x) {
    
    
    int now = root;
    while (1) {
    
    
        if (!now) return 0;
        if (T[now].val == x) {
    
    
            splay(now, root);
            return now;
        }
        int nxt = x < T[now].val ? 0 : 1;
        now = T[now].ch[nxt];
    }
}
void delet(int x) {
    
    
    int pos = find(x);
    if (!pos) return;
    if (T[pos].rec > 1) {
    
    
        T[pos].rec--, T[pos].size--;
        return;
    } else {
    
    
        if (!T[pos].ch[0] && !T[pos].ch[1]) {
    
    
            root = 0;
            return;
        } else if (!T[pos].ch[0]) {
    
    
            root = T[pos].ch[1];
            T[root].fa = 0;
            return;
        } else {
    
    
            int left = T[pos].ch[0];
            while (T[left].ch[1]) left = T[left].ch[1];
            splay(left, T[pos].ch[0]);
            connect(T[pos].ch[1], left, 1);
            connect(left, 0, 1);  //
            update(left);
        }
    }
}
int rak(int x) {
    
    
	return T[ls(find(x))].size + 1;
}
int arank(int x) {
    
    
    int now = root;
    while (1) {
    
    
        int tem_num = T[now].size - T[T[now].ch[1]].size;
        if (T[T[now].ch[0]].size < x && x <= tem_num) {
    
    
            splay(now, root);
            return T[now].val;
        }
        if (x < tem_num)
            now = T[now].ch[0];
        else
            now = T[now].ch[1], x -= tem_num;
    }
}
int lower(int x) {
    
    
    int now = root, ans = -inf;
    while (now) {
    
    
        if (T[now].val < x) ans = max(ans, T[now].val);
        int nxt = x <= T[now].val ? 0 : 1;  //这里需要特别注意
        now = T[now].ch[nxt];
    }
    return ans;
}
int upper(int x) {
    
    
    int now = root, ans = inf;
    while (now) {
    
    
        if (T[now].val > x) ans = min(ans, T[now].val);
        int nxt = x < T[now].val ? 0 : 1;
        now = T[now].ch[nxt];
    }
    return ans;
}
int main() {
    
    
    int N = read();
    while (N--) {
    
    
        int opt = read(), x = read();
        if (opt == 1)
            Insert(x);
        else if (opt == 2)
            delet(x);
        else if (opt == 3)
            printf("%d\n", rak(x));
        else if (opt == 4)
            printf("%d\n", arank(x));
        else if (opt == 5)
            printf("%d\n", lower(x));
        else if (opt == 6)
            printf("%d\n", upper(x));
    }
    return 0;
}

模板

#define ls(x) T[x].ch[0]
#define rs(x) T[x].ch[1]
#define fa(x) T[x].fa
#define root T[0].ch[1]
struct node {
    
    
    int fa;		//父节点
	int ch[2];	//0代表左儿子，1代表右儿子
	int val;	//权值
	int rec;	//这个权值的节点出现的次数
	int size;	//子节点的数量（包含这个点）
} T[maxn];
int tot = 0, pointnum = 0;
void update(int x) {
    
     T[x].size = T[ls(x)].size + T[rs(x)].size + T[x].rec; }
int ident(int x) {
    
     return T[fa(x)].ch[0] == x ? 0 : 1; }
void connect(int x, int fa, int how) {
    
    
    T[fa].ch[how] = x;
    T[x].fa = fa;
}
void rotate(int x) {
    
    
    int Y = fa(x), R = fa(Y);
    int Yson = ident(x), Rson = ident(Y);
    connect(T[x].ch[Yson ^ 1], Y, Yson);
    connect(Y, x, Yson ^ 1);
    connect(x, R, Rson);
    update(Y);
    update(x);
}
void splay(int x, int to) {
    
    
    to = fa(to);
    while (fa(x) != to) {
    
    
        int y = fa(x);
        if (T[y].fa == to)
            rotate(x);
        else if (ident(x) == ident(y))
            rotate(y), rotate(x);
        else
            rotate(x), rotate(x);
    }
}
int newnode(int v, int f) {
    
    
    T[++tot].fa = f;
    T[tot].rec = T[tot].size = 1;
    T[tot].val = v;
    return tot;
}
void Insert(int x) {
    
    
    int now = root;
    if (root == 0) {
    
     newnode(x, 0); root = tot; }
    else {
    
    
        while (1) {
    
    
            T[now].size++;
            if (T[now].val == x) {
    
    
                T[now].rec++;
                splay(now, root);
                return;
            }
            int nxt = x < T[now].val ? 0 : 1;
            if (!T[now].ch[nxt]) {
    
    
                int p = newnode(x, now);
                T[now].ch[nxt] = p;
                splay(p, root);
                return;
            }
            now = T[now].ch[nxt];
        }
    }
}
int find(int x) {
    
    
    int now = root;
    while (1) {
    
    
        if (!now) return 0;
        if (T[now].val == x) {
    
    
            splay(now, root);
            return now;
        }
        int nxt = x < T[now].val ? 0 : 1;
        now = T[now].ch[nxt];
    }
}
void delet(int x) {
    
    
    int pos = find(x);
    if (!pos) return;
    if (T[pos].rec > 1) {
    
    
        T[pos].rec--, T[pos].size--;
        return;
    } else {
    
    
        if (!T[pos].ch[0] && !T[pos].ch[1]) {
    
    
            root = 0;
            return;
        } else if (!T[pos].ch[0]) {
    
    
            root = T[pos].ch[1];
            T[root].fa = 0;
            return;
        } else {
    
    
            int left = T[pos].ch[0];
            while (T[left].ch[1]) left = T[left].ch[1];
            splay(left, T[pos].ch[0]);
            connect(T[pos].ch[1], left, 1);
            connect(left, 0, 1);  //
            update(left);
        }
    }
}
int rak(int x) {
    
    
	return T[ls(find(x))].size + 1;
}
int arank(int x) {
    
    
    int now = root;
    while (1) {
    
    
        int tem_num = T[now].size - T[T[now].ch[1]].size;
        if (T[T[now].ch[0]].size < x && x <= tem_num) {
    
    
            splay(now, root);
            return T[now].val;
        }
        if (x < tem_num)
            now = T[now].ch[0];
        else
            now = T[now].ch[1], x -= tem_num;
    }
}
int lower(int x) {
    
    
    int now = root, ans = -inf;
    while (now) {
    
    
        if (T[now].val < x) ans = max(ans, T[now].val);
        int nxt = x <= T[now].val ? 0 : 1;  //这里需要特别注意
        now = T[now].ch[nxt];
    }
    return ans;
}
int upper(int x) {
    
    
    int now = root, ans = inf;
    while (now) {
    
    
        if (T[now].val > x) ans = min(ans, T[now].val);
        int nxt = x < T[now].val ? 0 : 1;
        now = T[now].ch[nxt];
    }
    return ans;
}

猜你喜欢

转载自blog.csdn.net/weixin_42856843/article/details/109330669
今日推荐
周排行
爬虫苦训第二天，终篇！！！
分布式文件系统FastDFS在SpringBoot下的应用
MapReduce （8）--MapReduce 自定义outputFormat
论枢纽元的选择方式对快速排序性能的影响
乐优商城（三十七）——订单微服务
day10-函数进阶
Constructing Roads
un-植物：芨芨草
INSPIRED启示录 读书笔记 - 第24章 平滑部署
一个正规软件公司工作职责划分
每日归档
更多
2024-12-23(0)
2024-12-22(0)
2024-12-21(0)
2024-12-20(0)
2024-12-19(0)
2024-12-18(0)
2024-12-17(0)
2024-12-16(0)
2024-12-15(0)
2024-12-14(0)

代码天地 © 2018 codetd.com

境外服务器   最新电视剧2022