概述
234树和红黑树是完全等价的,红黑树本质上就是234树;由于234树是一棵高度平衡的树,实现起来比较复杂,所以一般通过红黑树来实现234树,而红黑树同样保证了O(logN)的时间内完成查找、插入和删除操作。
红黑树的定义
- 节点只能是黑色或者红色。
- 根节点必须是黑色。
- 每个叶子节点是黑色节点(称之为NIL节点,又被称为黑哨兵);可以理解为红黑树中每个节点都有两个子节点,除了黑色的空节点。
- 每个红色节点的两个子节点都是黑色(或者说从每个叶子节点到根的所有路径上不能有两个连续的红色节点)。
- 从任一节点到它所能到达的叶子节点的所有简单路径都包含相同数目的黑色节点。
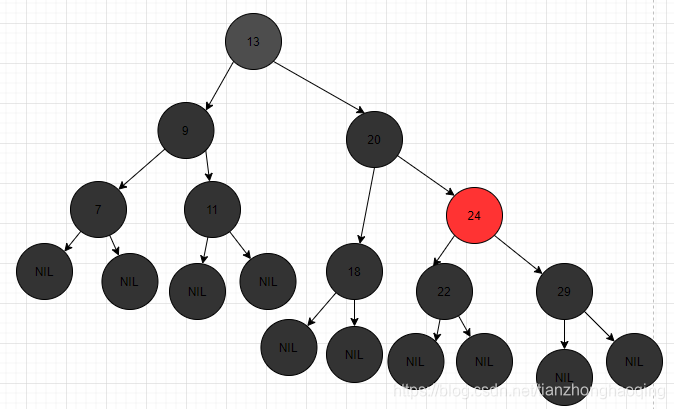
理解:
这些性质保证了根节点到任意叶子节点的路径长度,最长的不会超过最短的一倍。(因为所有路径上的黑色节点相等,差别在红色节点上,同时一条路径上的黑色节点一定比红色节点多)。
实际上大体来讲AVL树的插入,删除、查询的时间复杂度更红黑树是一样的。
有人说红黑树比AVL树性能好的原因是,红黑树节点的删除最多只旋转3次,而AVL树删除节点可能会不断的回溯到根,但这不是主要的原因。因为红黑树删除节点过程中也有可能需要不断回溯到根,只是不需要做那么导出旋转而已,但是旋转也不会耗费很大的性能,只是将节点的引用关系左旋改变而已,可以认为是O(1)。
红黑树比AVL树性能好的主要原因是,AVL树是高度平衡的树(左右子树高度差最多为1),所以不管是插入、删除都会很容易导致树的不平衡,从而引发频繁调整,而红黑树不是严格的平衡树,节点插入与删除,并不容易导致树的频繁调整,所以红黑树不会频繁调整才是红黑树综合性能比AVL树好的原因。
红黑树与234树的等价关系
234树中2,3,4节点与红黑树节点的等价关系
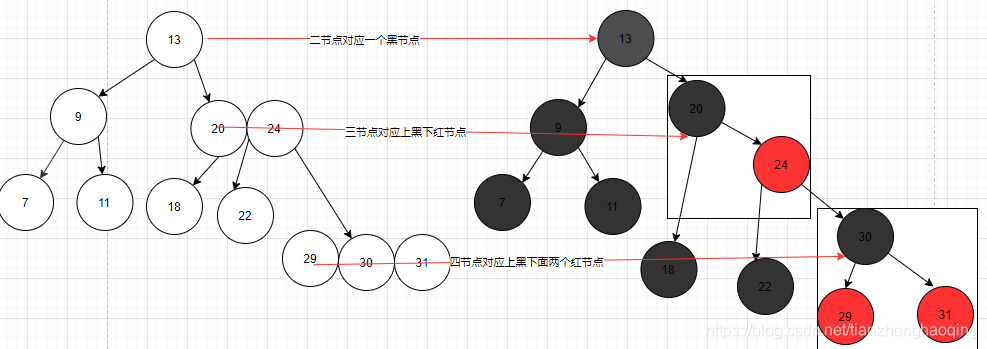
总共有4种等价关系,分别如下:
- 2节点对应红黑树上一个黑节点
- 3节点对应红黑树上两种状态,上黑下红
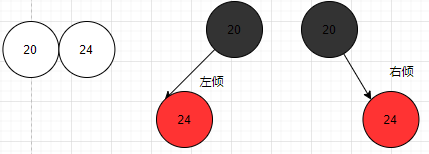
- 4节点对应红黑树上,上黑下两红
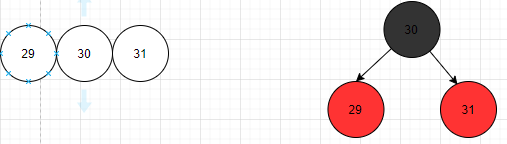
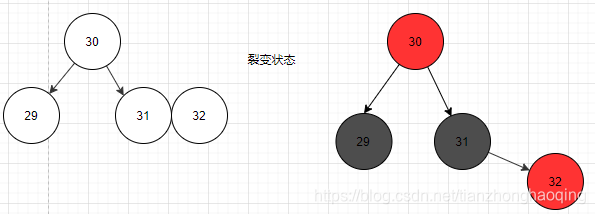
- 裂变状态下(中间状态,本身是4节点,现在又插入一个节点),上红下两黑
结合等价关系理解红黑树的定义
- 定义中第一条理解为:234树中只有2,3,4三种节点,根据等价关系发现只有红黑两种颜色。
- 定义中第二条理解为:红黑树的根只能是234树中的2,3,4三种节点,根据等价关系转换发现根只能是黑色。
- 定义中第三、四条理解为:通过等价关系,红黑树中红色节点向上收缩找到黑节点转换成234树,发现所有的叶子节点和红色节点的子节点都是234树上的2节点,因此所有叶子节点和红色节点的子节点只能是黑色。
- 定义中第5条理解为(黑平衡):红黑树转换成234树后,所有的叶子节点都在同一层,同时234树中每个节点只有一个红黑树的黑色节点;发现每个节点到它的所有叶子节点都经过相同的层数,因此叶子节点数相同。
参考
- https://blog.csdn.net/qq_25940921/article/details/82184055
- https://www.cnblogs.com/nullzx/p/6128416.html
- https://www.bilibili.com/video/BV135411h7wJ?p=5