文章目录
一、前言
对于求取一元函数y = f(x)的极值问题,我们可以利用暴力的手段,通过细分自变量x的定义域区间,不断带入函数表达式中比较结果得到近似的最优解。这样的方法最大的好处就是简单,但是随之带来的问题就是收敛速度极大地受区间细分程度的影响。那么遗传算法是如何解决这个问题的呢?以下是从这个问题出发,我对遗传算法的一些理解。
二、遗传算法思想
在自然界中存在“物竞天择,优胜劣汰”的自然法则,各个物种总是倾向于留存自己优良的基因,而遗传算法正是借鉴这种思想,将一个最优解求取的问题抽象化为一个种群的演变过程,其中涉及到种群、个体、染色体和基因等概念,并针对不同问题将其实例化,完成对可行解的生成、比较、挑选和淘汰,从而得到最优解。
三、遗传算法组成
下表是我理解的生物遗传与遗传算法的概念对比:
| 生物遗传概念 | 遗传算法概念 |
|---|---|
| 个体 | 可行解 |
| 染色体 | 可行解的编码 |
| 基因 | 可行解的编码各分量 |
| 种群 | 可行解的集合 |
| 最强个体 | 最优解 |
| 婚配 | 编码某些分量的交叉操作 |
| 变异 | 编码某些分量的偶发变化 |
| 适应性 | 对可行解的评价结果 |
3.1 编码与染色体
在上表的基础上,针对遗传算法在一元函数 y = x + 10 s i n ( 5 x ) + 7 c o s ( 4 x ) 在 区 间 x ∈ [ 0 , 9 ] y = x+10sin(5x)+7cos(4x)在区间x∈[0,9] y=x+10sin(5x)+7cos(4x)在区间x∈[0,9]上的极值及极值点求解问题,作如下阐述:
假设我们想要得到的极值点x坐标的精度为小数点后4位,对于定义域 x ∈ [ 0 , 9 ] x∈[0,9] x∈[0,9],我们需要将其细分为 ( 9 − 0 ) ∗ 1 0 4 = 90000 (9-0)*10^4 = 90000 (9−0)∗104=90000份,那么可行解就在这90000份中。我们知道 2 16 < 90000 < 2 17 2^{16} < 90000 < 2^{17} 216<90000<217,所以要想用二进制数表示所有的可行解,我们需要至少需要17bits。而这一个17bits的数,就是我们对可行解的编码,每1bit就是我们假设的单个基因,一个完整的编码就看作是由这17个基因构成的一条染色体(chromosome)。当然,编码的形式不仅限于二进制数,还可以直接采用格雷码、实数编码等方式。
如何将完成可行解与编码之间的相互转换呢?假设 y = f ( x ) , x ∈ [ a , b ] y = f(x),x ∈ [ a, b] y=f(x),x∈[a,b],chr_x为x对应的n位二进制数编码,对于chr_x与x之间,有如下一般化解码关系:
x = a + D E C ( c h r _ x ) ∗ a − b 2 n − 1 (1) x = a + DEC(chr\_x)* \frac{a-b}{2^n-1} \tag{1} x=a+DEC(chr_x)∗2n−1a−b(1)
其中 D E C ( ) DEC() DEC() 为将二进制数转为十进制数的函数
对于本问题而言,解码关系为:
x = 0 + D E C ( c h r _ x ) ∗ 9 − 0 2 17 − 1 (2) x = 0 + DEC(chr\_x)* \frac{9-0}{2^{17}-1} \tag{2} x=0+DEC(chr_x)∗217−19−0(2)
3.2 个体与种群
自然界中大多数生物具有多条染色体,而对于一元函数 f ( x ) f(x) f(x)的极值问题而言,单个个体(可行解)仅含有一条染色体( x x x的编码),进一步,若要求一个空间平面的极值,也就是二元函数 f ( x , y ) f(x,y) f(x,y)的极值问题,则单个个体包含两条染色体( x x x的编码和 y y y 的编码)。若干个体的集合组成了一个种群,其含义为解空间的一个子空间,对于一元函数极值问题而言,就是定义域中的某个点集。
3.3 适应性与适应性函数
在自然界中,一个物种是否能够繁荣却决于其对环境的适应能力。在遗传算法中,我们用适应性函数评价一个解的优劣,在函数极值问题中,适应性函数就是待求解函数表达式,解对应的函数值越大,则适应性越高,反映解的质量越好。一个问题的求解快慢和好坏,与适应性函数的选取有很大关系。
3.4 遗传与进化
生物繁衍的本质是基因的传递,也就是所谓的遗传过程。要想本物种能够长久地生存下去,生物不得不发生进化,而所谓的进化过程,就是在种群中淘汰掉适应性差的个体,筛选出优秀的个体,在这些优秀的个体之间进行婚配,使得彼此的优质基因进行重组,甚至利用偶发的变异来产生更加优秀的基因。在遗传算法中,我们通过下面的方法使得 解 能够“进化”:
- 【1】选择
通过对比当前代种群中各个体(可行解)按照适应性高低,利用适当的选取方式,比如轮盘赌、精英机制等,挑选出优胜的个体作为父母本体; - 【2】交叉
将【1】中得到的父母本的染色体(可行解的子变量)上的基因(编码的分量)进行按照一定概率发生部分交换,比如单点交换、多点交换等,从而产生新一代个体(新的可行解); - 【3】变异
在【2】的基础上,按照一定概率在某些新一代个体的染色体基因上发生突变,比如单点按位取反等方式,从而产生变异的新一代个体(新的可行解)。不过通常变异得到的个体出现适应性很高的可能性极小,因此设置变异的概率是远小于交叉的设定概率的,这一点与自然界中的生物进化是类似的。
3.5 遗传算法的一般步骤
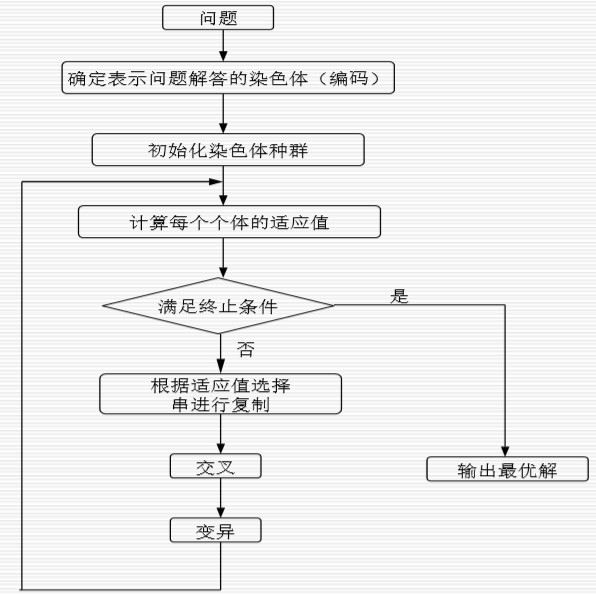
四、MATLAB实现一元函数极值的遗传算法求解
参考程序 matlab_ga,求解
y = x + 10 s i n ( 5 x ) + 7 c o s ( 4 x ) (3) y = x+10sin(5x)+7cos(4x) \tag{3} y=x+10sin(5x)+7cos(4x)(3)
在区间 x ∈ [ 0 , 9 ] x∈[0,9] x∈[0,9]上的极值。
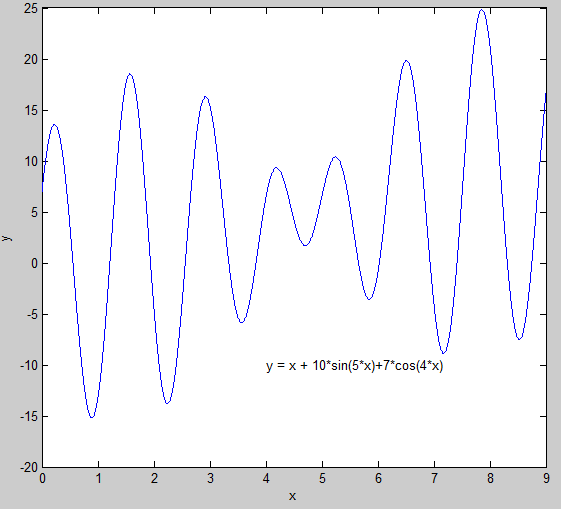
4.1 初始参数定义说明
一个问题的求解理解为一个种群不断进化的过程,开始进化前,各初始参数定义如下:
| 参数名 | 初始值 | 含义 |
|---|---|---|
| p o p u l a t i o n _ s i z e population\_size population_size | 100 | 种群中单代所含个体数,即一次迭代所含可行解个数 |
| c h r o m o s o m e _ s i z e chromosome\_size chromosome_size | 17 | 一条染色体上所含基因数,即单个可行解的编码长度 |
| g e n e r a t i o n _ s i z e generation\_size generation_size | 200 | 种群繁衍代数,即迭代代数 |
| c r o s s _ r a t e cross\_rate cross_rate | 0.6 | 交叉率,即编码发生交叉互换的概率 |
| m u t a t e _ r a t e mutate\_rate mutate_rate | 0.01 | 变异率,即单个基因发生突变的概率 |
| e l i t i s m elitism elitism | t r u e true true | 是否挑选精英,即是否将每一代适应性最高的个体保留 |
4.2 进化过程变量定义说明
在进化过程我们需要不断比较种群内各个体之间的适应性高低,并且筛选出合适的个体进行繁衍,因此有如下定义:
| 参数名 | 类型 | 含义 |
|---|---|---|
| G | 单变量 | 当前繁衍代数,即当前迭代次数 |
| f i t n e s s _ v a l u e fitness\_value fitness_value | 1 x p o p u l a t i o n _ s i z e population\_size population_size 维矩阵 | 当代各个体的适应度 |
| p o p u l a t i o n population population | p o p u l a t i o n _ s i z e population\_size population_size x c h r o m o s o m e _ s i z e chromosome\_size chromosome_size 维矩阵 | 当代各个体基因情况 |
| f i t n e s s _ s u m itness\_sum itness_sum | 1 x p o p u l a t i o n _ s i z e population\_size population_size 维矩阵 | 当代前i个个体的适应度之和情况 |
| f i t n e s s _ a v e r a g e fitness\_average fitness_average | G G G x 1 维矩阵 | 各代平均适应度 |
| b e s t _ f i t n e s s best\_fitness best_fitness | 单变量 | 覆盖存储历代得到的最优个体的适应度 |
| b e s t _ i n d i v i d u a l best\_individual best_individual | 1 x c h r o m o s o m e _ s i z e chromosome\_size chromosome_size | 覆盖存储历代得到的最优个体的染色体基因情况(最优解) |
| b e s t _ g e n e r a t i o n best\_generation best_generation | 单变量 | 最优个体产生的代数 |
4.3 主过程(genetic_algorithm.m)
- 初始化种群
- 包含种群大小(即单代个体数)、染色体长度(即编码长度)、繁衍代数(即总迭代次数)、交叉概率、变异概率、是否选择精英操作等
- 生成第一批个体
- 在init.m中,通过对 p o p u l a t i o n ( i , j ) population(i,j) population(i,j)进行随机赋值(0或者1),产生第一批共计100个个体:

- 主循环
- 对每一代执行 适应度计算、个体排序、个体选择、染色体交叉和基因变异五个步骤,直到设定的繁衍代数达到而终止。
for G=1:generation_size
fitness(population_size, chromosome_size); % 计算种群每代各个体的适应度
rank(population_size, chromosome_size); % 对个体按适应度大小进行排序
selection(population_size, chromosome_size, elitism); % 选择操作
crossover(population_size, chromosome_size, cross_rate);% 交叉操作
mutation(population_size, chromosome_size, mutate_rate);% 变异操作
end
以初始化第一批个体后截下来的繁衍第二代举例进行如下解释:
4.4 适应度计算(fitness.m)
利用3.1节的解码公式(2),对当前代个个体的基因编码 p o p u l a t i o n ( i , : ) population(i, :) population(i,:)进行可以解码转换为实数的可行解,带入函数表达式(3)得到当前代各个体的适应度 f i t n e s s _ v a l u e ( i ) fitness\_value(i) fitness_value(i):
for i=1:population_size
for j=1:chromosome_size
% 给population的i行j列赋值
population(i,j) = round(rand); % rand产生(0,1)之间的随机数,round()是四舍五入函数
end
end
4.5 个体排序(rank.m)
- 使用冒泡法,依据4.4节所得到的 f i t n e s s _ v a l u e ( i ) fitness\_value(i) fitness_value(i)将当前代各个体由低到高排序,即依照 f i t n e s s _ v a l u e fitness\_value fitness_value值的大小将 p o p u l a t i o n ( i , : ) population(i, :) population(i,:)重排;
- 由重排结果计算得到前i个个体的适应度之和 f i t n e s s _ s u m ( i ) fitness\_sum(i) fitness_sum(i),比如 f i t n e s s _ s u m ( 1 ) fitness\_sum(1) fitness_sum(1)为第1个个体的适应度, f i t n e s s _ s u m ( 2 ) fitness\_sum(2) fitness_sum(2)为第1个和第2个个体的适应度之和,以此类推;
- 保存当前代(第 G G G代)的平均适应度 f i t n e s s _ a v e r a g e ( G ) fitness\_average(G) fitness_average(G)
4.5 个体选择(select.m)
- 寻找优良个体
-
轮盘赌简介
- 随机转动一下轮盘,当轮盘停止转动时,若指针指向某个个体,则该个体被选中
- 单次挑选步骤举例:
- 假设个体适应度 f i t n e s s _ v a l u e [ 5 ] : 0.1 , 0.1 , 0.1 , 0.1 , 0.1 fitness\_value[5]:0.1,0.1,0.1,0.1,0.1 fitness_value[5]:0.1,0.1,0.1,0.1,0.1
- 前i项求和得到适应度之和 f i t n e s s _ s u m [ 5 ] : 0.1 , 0.2 , 0.3 , 0.4 , 0.5 fitness\_sum[5]:0.1,0.2,0.3,0.4,0.5 fitness_sum[5]:0.1,0.2,0.3,0.4,0.5
- 产生位于0和最大适应度和之间的随机数 r ∈ [ 0 , 0.5 ] r ∈[0, 0.5] r∈[0,0.5],比如 0.23 0.23 0.23
- 二分法查找最接近 0.23 0.23 0.23 的个体序号
- 初始下限 f i r s t = 1 first = 1 first=1,上限 l a s t = 5 last = 5 last=5,中间 m i d = r o u n d ( ( f i r s t + l a s t ) / 2 ) = 3 mid = round((first + last)/2) = 3 mid=round((first+last)/2)=3
- 第一次循环:
0.23 < f i t n e s s _ s u m [ m i d ] = 0.3 0.23 < fitness\_sum[mid] = 0.3 0.23<fitness_sum[mid]=0.3,更新 l a s t = 3 , m i d = ( 1 + 3 ) / 2 = 2 last = 3,mid = (1+3)/2 = 2 last=3,mid=(1+3)/2=2,进入下一次循环 - 第二次循环:
0.23 > f i t n e s s _ s u m [ m i d ] = 0.2 0.23 > fitness\_sum[mid] = 0.2 0.23>fitness_sum[mid]=0.2, 更新 f i r s t = 2 first = 2 first=2,此时 l a s t = 3 last = 3 last=3,两者不可再二分 - 故设被选择的个体序号为 i d x = l a s t = 3 idx = last = 3 idx=last=3(选择 i d x = f i r s t = 2 idx = first = 2 idx=first=2不是不可以,但是我们更倾向于选择适应度更高的个体),当个体数更多时同理。
- 当个体适应度不均等时,比如 1 , 1 , 1 , 1 , 10000 1,1,1,1,10000 1,1,1,1,10000,对应的适应度前i项和则为 1 , 2 , 3 , 4 , 10004 1,2,3,4,10004 1,2,3,4,10004,那么随机产生的r就会有极大的可能落在 [ 4 , 10004 ] [4,10004] [4,10004]之间,我们就极有可能选择到最后一个个体,这也是具有较高适应度的个体比具有较低适应度的个体更有机会被选中的原因,不过若是运气不好随机到了 [ 1 , 4 ] [1,4] [1,4] 之间的数,则就有可能错过适应度更高的个体。
- 多次挑选:
- 重复单次挑选步骤 p o p u l a t i o n _ s i z e population\_size population_size次,得到 p o p u l a t i o n _ s i z e population\_size population_size个新一代备选个体保存在 p o p u l a t i o n _ n e w [ ] population\_new[] population_new[]中。
-
非精英 / 精英选择
- 非精英选择:产生下一代种群个体 p o p u l a t i o n [ ] population [] population[],默认 p o p u l a t i o n _ s i z e population\_size population_size 个个体全部复制自轮盘赌挑选出来的个体集合 p o p u l a t i o n _ n e w [ ] population\_new[] population_new[]。
- 精英选择:前 p o p u l a t i o n _ s i z e – 1 population\_size – 1 population_size–1 个个体仍然复制轮盘赌挑选得到的个体,而第 p o p u l a t i o n _ s i z e population\_size population_size 个个体的基因延用当前代排序后的最后一个个体的基因,即所谓的保留优良个体基因。
-
4.6 染色体交叉(crossover.m)
染色体交叉操作发生在任意两个个体之间,常见的交叉方式有单点交叉、多点交叉和部分匹配交叉等。以含单染色体的个体的单点交叉为例:
- 生成随机概率 r a n d ∈ [ 0 , 1 ] rand∈[0,1] rand∈[0,1],当 r a n d > c r o s s _ r a t e rand > cross\_rate rand>cross_rate 时,执行交叉操作
- 单点交叉操作:
- 生成随机交叉位置 r a n d c r o s s _ p o s i t i o n ∈ [ 0 , c h r o m o s o m e _ s i z e ] randcross\_position∈[0,chromosome\_size] randcross_position∈[0,chromosome_size]
- 将两个个体的染色体上位于 r a n d c r o s s _ p o s i t i o n randcross\_position randcross_position上及之后的基因互换:
- 如下表,若 r a n d c r o s s _ p o s i t i o n = 3 randcross\_position = 3 randcross_position=3,即 A , B A, B A,B交叉操作发生在第4位,则交叉过后的结果为 A ′ , B ′ A', B' A′,B′:
| A : 111 000 ‾ A: 1 1 1 \underline{0 0 0} A:111000 | A ′ : 111 111 ‾ A': 1 1 1 \underline{1 1 1} A′:111111 |
|---|---|
| B : 000 111 ‾ B: 0 0 0 \underline{1 1 1} B:000111 | B ′ : 000 000 ‾ B': 0 0 0 \underline{0 0 0} B′:000000 |
- 对种群单代 p o p u l a t i o n [ ] population [] population[] 中 p o p u l a t i o n _ s i z e population\_size population_size个个体两两一组执行随机交叉操作;
- 通过这样的交叉操作,能够避免后代过于强势而出现过早收敛(因为适应度高所以被选中的几率更大)。
4.7 基因变异(mutation.m)
基因变异发生在单个个体的单条染色体上,常见的变异方式有位点变异、逆转变异、插入变异等。以位点变异为例:
- 位点变异单次操作:
- 生成随机概率 r a n d ∈ [ 0 , 1 ] rand∈[0,1] rand∈[0,1],当 r a n d > m u t a e _ r a t e rand > mutae\_rate rand>mutae_rate 时,执行变异操作
- 生成随机变异位置 m u t a t e _ p o s i t i o n ∈ [ 0 , c h r o m o s o m e _ s i z e ] mutate\_position∈[0,chromosome\_size] mutate_position∈[0,chromosome_size]
- 将染色体 m u t a t e _ p o s i t i o n mutate\_position mutate_position处的基因取反:
- 以下表为例,若 m u t a t e _ p o s i t i o n = 1 mutate\_position = 1 mutate_position=1,则 A A A变异操作发生在第2位,变异结果为 A ′ A' A′:
| A A A | A ′ A' A′ |
|---|---|
| 1 ‾ 11111 \underline{1}11111 111111 | 0 ‾ 11111 \underline{0}11111 011111 |
- 位点变异多次操作:
- 对 p o p u l a t i o n [ ] population [] population[] 中 p o p u l a t i o n _ s i z e population\_size population_size 个个体重复位点变异单次操作
4.8 求解结果
重复 4.4 - 4.8 节步骤 g e n e r a t i o n _ s i z e generation\_size generation_size次,得到函数(3)极值最终求解结果。由于求解过程的随机性,因此每次最优结果的迭代次数都有所不同:

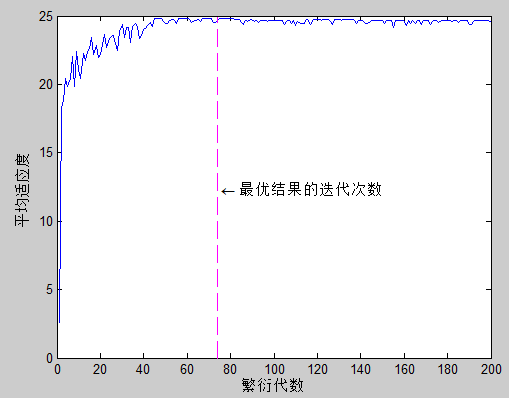
取一次输出结果进行验证:

- 最优个体染色体基因构型: 1 0101 1110 1111 1011 1\;0101\;1110\;1111\;1011 10101111011111011
- 注意该基因构型转换为十进制时,低位在前,高位在后,即:
x _ t m p = D E C ( 1101 1111 0111 1010 1 ) = 1 ∗ 2 0 + 0 ∗ 2 1 + 1 ∗ 2 2 + . . . + 1 ∗ 2 15 + 1 ∗ 2 16 = 114421 x\_tmp = DEC(1101\;1111\;0111\;1010\;1) =1*2^0+0*2^1 +1*2^2 + ... + 1*2^{15} + 1*2^{16} = 114421 x_tmp=DEC(11011111011110101)=1∗20+0∗21+1∗22+...+1∗215+1∗216=114421

- 按照解码公式得,最有个体对应自变量值,该结果与matlab解码结果是吻合的:
x = 0 + x _ t m p ∗ 9 − 0 2 17 − 1 ≈ 7.8567 x = 0 + x\_tmp * \frac{9 - 0}{2^{17} - 1} ≈7.8567 x=0+x_tmp∗217−19−0≈7.8567
