卡尔曼滤波学习路线
1. 原理
卡尔曼滤波(Kalman filtering)是一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响,所以最优估计也可看作是滤波过程。
2. 目的
这篇文章主要是自己同样在学习 Kalman filter 的过程中,总结出一套学习的路线,能够让你在了解 Kalman filter 能够有一个清晰的路线,当然这边也是转载了各位博主的资料,这里说声谢谢。
3. 推荐
视频与博文二选一即可,必看精品哦!
4. 公式
4.1 说明
- 出现
^代表的是 估计状态。

4.1.1 公式一
x ^ k = F k ∗ x ^ k − 1 + u ⃗ k ∗ B k {\color{fuchsia}\hat{x}_k}=F_k*{\color{blue}\hat{x}_{k-1}}+{\color{green}\vec{u}_k}*B_k x^k=Fk∗x^k−1+uk∗Bk
- x ^ k \color{fuchsia}\hat{x}_k x^k:当前最优估计(即均值,其他地方常用 μ \mu μ)
- F k F_k Fk:系数
- x ^ k − 1 {\color{blue}\hat{x}_{k-1}} x^k−1:前一刻最优估计
- B k B_k Bk:系数
- u ⃗ k {\color{green}\vec{u}_k} uk:已知外部控制量
4.1.2 公式二
P k = F k ∗ P k − 1 ∗ F k T + Q k {\color{fuchsia}P_k}=F_k*{\color{blue}P_{k-1}}*F_k^T + {\color{red}Q_k} Pk=Fk∗Pk−1∗FkT+Qk
- P k {\color{fuchsia}P_k} Pk:当前不确定性(估计误差协方差)
- F k F_k Fk:系数
- P k − 1 {\color{blue}P_{k-1}} Pk−1:前一刻不确定性
- F k T F_k^T FkT:系数
- Q k {\color{red}Q_k} Qk:外部环境干扰
总公式
x ^ k = F k ∗ x ^ k − 1 + u ⃗ k ∗ B k P k = F k ∗ P k − 1 ∗ F k T + Q k {\color{fuchsia}\hat{x}_k}=F_k*{\color{blue}\hat{x}_{k-1}}+{\color{green}\vec{u}_k}*B_k \\ {\color{fuchsia}P_k}=F_k*{\color{blue}P_{k-1}}*F_k^T + {\color{red}Q_k} x^k=Fk∗x^k−1+uk∗BkPk=Fk∗Pk−1∗FkT+Qk
由上式可知:
-
当前的最优估计( x ^ k \color{fuchsia}\hat{x}_k x^k)是根据前一刻最优估计( x ^ k − 1 {\color{blue}\hat{x}_{k-1}} x^k−1)预测得到的,并且加上已知外部控制量( u ⃗ k {\color{green}\vec{u}_k} uk)的修正。
-
而当前不确定性( P k {\color{fuchsia}P_k} Pk)由前一刻不确定性( P k − 1 {\color{blue}P_{k-1}} Pk−1)预测得到的,并加上外部环境干扰( Q k {\color{red}Q_k} Qk)。
至此,我们对系统可能的动向有了一个模糊的估计,用 x ^ k \color{fuchsia}\hat{x}_k x^k和 P k {\color{fuchsia}P_k} Pk 来表示。
4.1.3 公式三
如果再结合传感器的数据会怎样呢?
x ^ k ′ = x ^ k + K ′ ∗ ( z ⃗ k − H k ∗ x ^ k ) {\color{blue}\hat{x}'_k}={\color{fuchsia}\hat{x}_k}+{\color{purple}K'}*({\color{green}\vec{z}_k} - {\color{fuchsia}H_k}*{\color{fuchsia}\hat{x}_k}) x^k′=x^k+K′∗(zk−Hk∗x^k)
预测值:粉色
传感器测量值:绿色
- x ^ k ′ {\color{blue}\hat{x}'_k} x^k′:最新最优估计
- x ^ k {\color{fuchsia}\hat{x}_k} x^k:当前最优估计(即均值,其他地方常用 μ \mu μ)
- K ′ {\color{purple}K'} K′:卡尔曼控制增益
- z ⃗ k {\color{green}\vec{z}_k} zk:分布的均值,读取到的传感器数据
- H k {\color{fuchsia}H_k} Hk:矩阵(表示传感器数据)
4.1.4 公式四
P k ′ = P k − K ′ ∗ H k ∗ P k {\color{blue}{ {P}'_k}} = {\color{red}{P_k}}- {\color{purple}{K'}}* {\color{red}{H}_k}* {\color{red}{P}_k} Pk′=Pk−K′∗Hk∗Pk
-
P k ′ {\color{blue}{ {P}'_k}} Pk′:最新不确定性
-
P k {\color{red}{P_k}} Pk:当前不确定性
-
K ′ {\color{purple}K'} K′:卡尔曼增益
-
H k {\color{red}{H}_k} Hk:矩阵(表示传感器数据)
4.1.5 公式五
K ′ = P k ∗ H k T ∗ ( H k ∗ H k T ∗ P k + R k ) − 1 {\color{purple}{K'}}= {\color{red}{P_k}}* {\color{red}{H_k}^T}* ({\color{red}{H_k}}* {\color{red}{H_k}^T}* {\color{red}{P_k}}+ {\color{green}{R_k}} )^{-1} K′=Pk∗HkT∗(Hk∗HkT∗Pk+Rk)−1
- K ′ {\color{purple}{K'}} K′:卡尔曼增益
- P k {\color{red}{P_k}} Pk:当前不确定性
- H k T {\color{red}{H_k}^T} HkT:
- H k {\color{red}{H_k}} Hk:
- R k {\color{green}{R_k}} Rk:不确定性用协方差(表示传感器噪声)
总公式
x ^ k ′ = x ^ k + K ′ ∗ ( z ⃗ k − H k ∗ x ^ k ) P k ′ = P k − K ′ ∗ H k ∗ P k K ′ = P k ∗ H k T ∗ ( H k ∗ H k T ∗ P k + R k ) − 1 {\color{blue}\hat{x}'_k}={\color{fuchsia}\hat{x}_k}+{\color{purple}K'}*({\color{green}\vec{z}_k} - {\color{fuchsia}H_k}*{\color{fuchsia}\hat{x}_k}) \\ {\color{blue}{ {P}'_k}} = {\color{red}{P_k}}- {\color{purple}{K'}}* {\color{red}{H}_k}* {\color{red}{P}_k} \\ {\color{purple}{K'}}= {\color{red}{P_k}}* {\color{red}{H_k}^T}* ({\color{red}{H_k}}* {\color{red}{H_k}^T}* {\color{red}{P_k}}+ {\color{green}{R_k}} )^{-1} x^k′=x^k+K′∗(zk−Hk∗x^k)Pk′=Pk−K′∗Hk∗PkK′=Pk∗HkT∗(Hk∗HkT∗Pk+Rk)−1
上式给出了完整的更新步骤方程。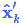
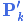
调整 K ′ {\color{purple}{K'}} K′使得状态误差协方差( P k ′ {\color{blue}{ {P}'_k}} Pk′)最小。(也就是使测量值和估算的误差最小化)
5. 框图

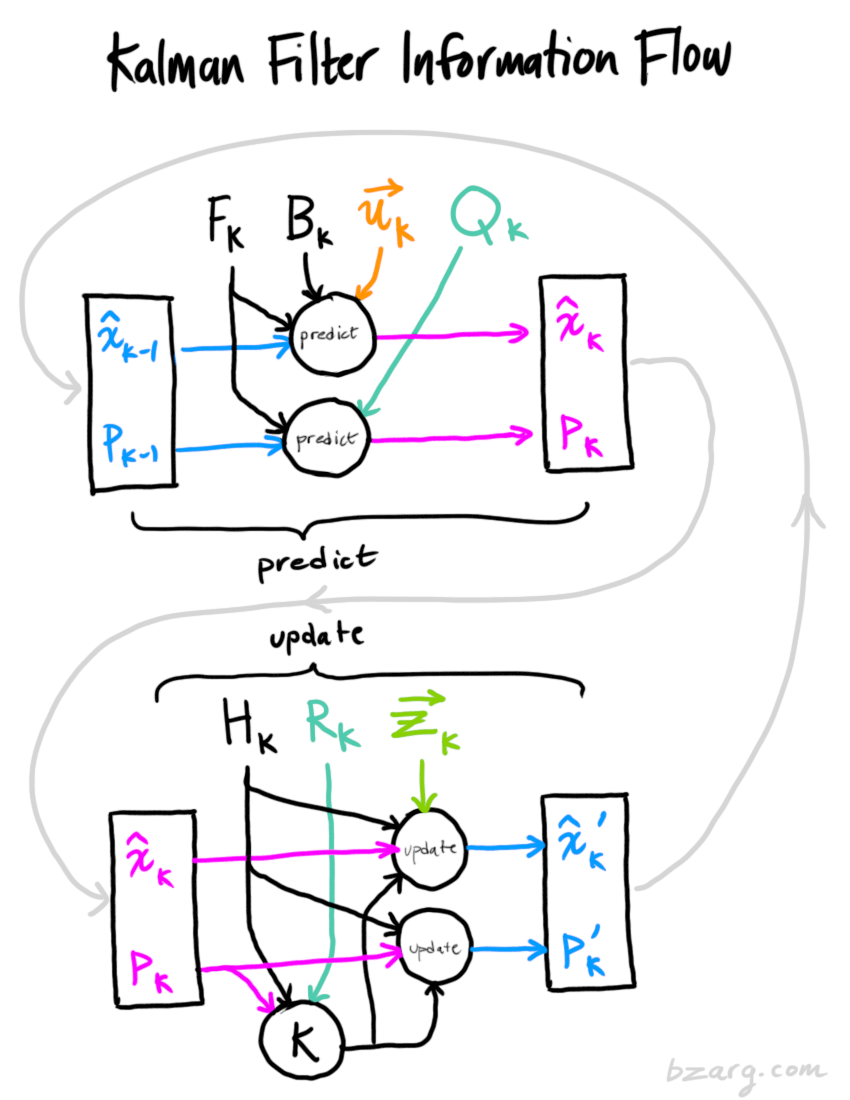
6. 代码
请跳转至,源码MD说明。
/*
举例而言,R固定,Q越大,代表越信任侧量值,Q无穷代表只用测量值;反之,Q越小代表越信任模型预测值,Q为零则是只用模型预测。
*/
typedef struct {
float x; /* state */
float A; /* x(n)=A*x(n-1)+u(n),u(n)~N(0,q) */
float H; /* z(n)=H*x(n)+w(n),w(n)~N(0,r) */
float q; /* process(predict) noise convariance */
float r; /* measure noise convariance */
float p; /* estimated error convariance */
float gain;
} kalman1_state;
void kalman1_init(kalman1_state *state, float init_x, float init_p)
{
state->x = init_x; // 待测量的初始值,如有中值一般设成中值(如陀螺仪)
state->p = init_p; // 后验状态估计值误差的方差的初始值
state->A = 1;
state->H = 1;
state->q = 2e2; // 预测噪声协方差
state->r = 5e2; // 检测误差协方差
}
float kalman1_filter(kalman1_state *state, float z_measure)
{
/* Predict */
// 公式请对照总公式,就能够清楚知道意思了
state->x = state->A * state->x;
state->p = state->A * state->A * state->p + state->q;
/* Measurement */
// 公式请对照总公式,就能够清楚知道意思了
state->gain = state->p * state->H / (state->p * state->H * state->H + state->r);
state->x = state->x + state->gain * (z_measure - state->H * state->x);
state->p = (1 - state->gain * state->H) * state->p;
return state->x;
}
7. MATLAB
MATLAB 是美国 MathWorks 公司出品的商业数学软件,用于数据分析、无线通信、深度学习、图像处理与计算机视觉、信号处理、量化金融与风险管理、机器人,控制系统等领域。在这里,我们用matlab来生成数据波形图,能够更加直观的看到卡尔曼滤波之后的波形。

7.1 使用说明
MATLAB官方为新用户提供了30天免费使用,且无需安装软件,新用户只需要注册并激活,就可以使用了。(这里具体教程就不讲解)matlab官网
那我们这里主要教大家如何使用,添加文件、编译程序、最后生成上面所描述的波形。(同样,也可以使用特定的波形助手工具等方式生成)
- 新建脚本,把代码当中
plot_result.m文件内容复制到新建脚本里面,且按Ctrl+s保存脚本,并命名为xxx.m

- 然后重复上面操作新建脚本,且把收集的数据复制到新建脚本里面,且按Ctrl+s保存文件,并命名为result.txt。

- 最后,双击回击到.m文件当中,这个时候运行按键显示正常,点击运行,稍等几秒,将会生成波形图,也就是我们刚开始看到的画面。(如果有同学无法生成最终波形图,可能是由于网络波动导致的)
