二叉树Oj题

题目

序号	题目	难度	本文	外链	方法
1.	单值二叉树	简单	跳转	LeetCode	递归
2.	二叉树深度	简单	跳转	LeetCode	递归
3.	翻转二叉树	简单	跳转	LeetCode	递归
4.	相同的树	简单	跳转	LeetCode	递归
5.	是否为子树	简单	跳转	LeetCode	递归
6.	对称二叉树	简单	跳转	LeetCode	递归
7.	平衡二叉树	简单	跳转	LeetCode	递归
8.	重建二叉树	中等	跳转	牛客	递归

---

单值二叉树

题目

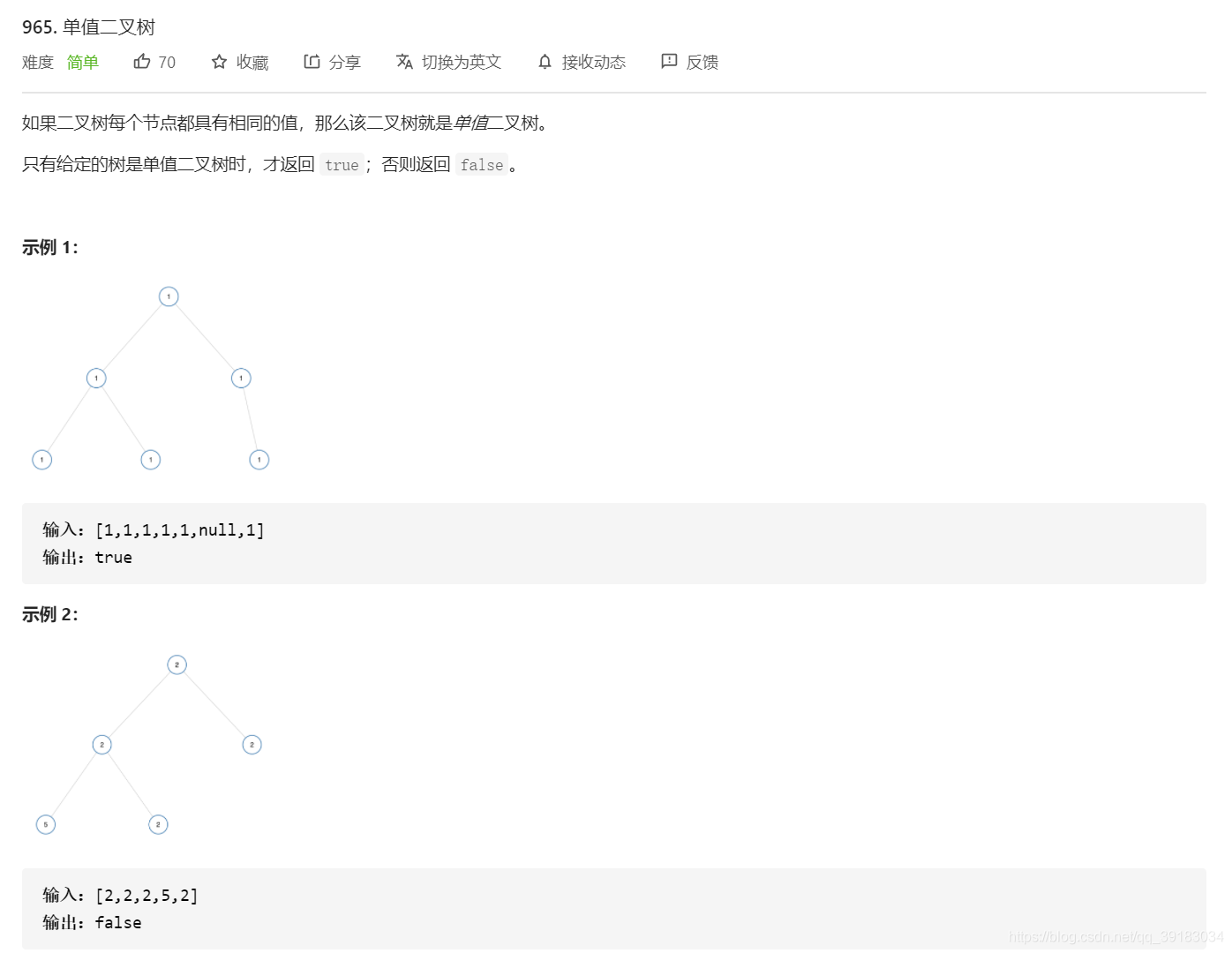
解法一

本题解法很简单，把任何一颗树看作当前树+子树。判断当前树时，如果左孩子存在，同时左孩子的值和根节点值不同返回false，如果右孩子存在，同时右孩子的值和根节点值不同返回false。最后对子树进行递归，也即return 左子树&&右子树，有一颗树出现false，整个树不是单值二叉树
其中注意：空树属于单值二叉树

bool isUnivalTree(struct TreeNode* root)
{
    
    
    if(root==NULL)
        return true;
    if(root->left&&root->val!=root->left->val)
        return false;
    if(root->right&&root->val!=root->right->val)
        return false;
    return isUnivalTree(root->left)&&isUnivalTree(root->right);


}

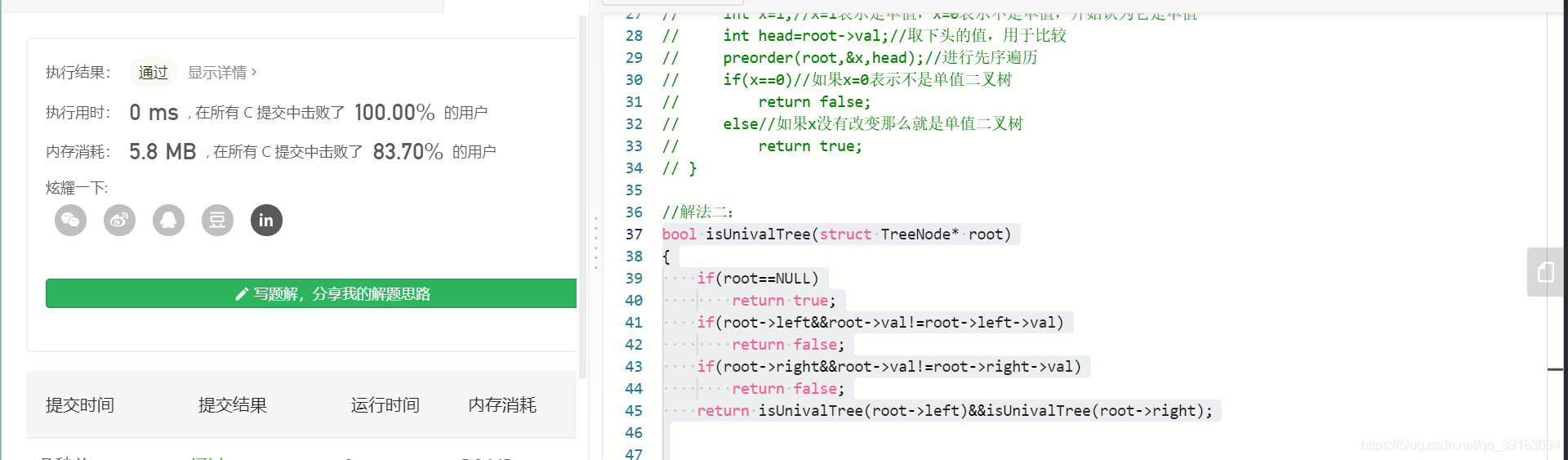
解法二
还是用递归，使用标记的方法进行。开始默认它是单值二叉树，然后进入递归，此过程访问结点，用结点的值和根节点比较，如果不同，修改这个标记，直到递归结束，在主函数内判断，若标记不是原来的值了，则不是单值二叉树，如果没有改变，则是单值二叉树。注意传入标记时，使用地址

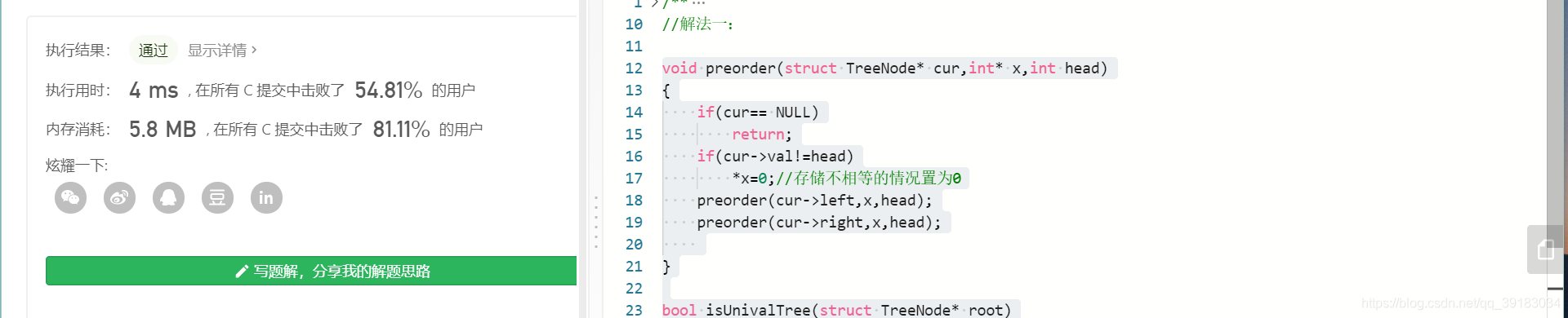
void preorder(struct TreeNode* cur,int* x,int head)
{
    
    
    if(cur== NULL)
        return;
    if(cur->val!=head)
        *x=0;//存储不相等的情况置为0
    preorder(cur->left,x,head);
    preorder(cur->right,x,head);
    
}

bool isUnivalTree(struct TreeNode* root)
{
    
    
    if(root==NULL)//空树，不是单值二叉树
        return false;
    int x=1;//x=1表示是单值，x=0表示不是单值，开始认为它是单值
    int head=root->val;//取下头的值，用于比较
    preorder(root,&x,head);//进行先序遍历
    if(x==0)//如果x=0表示不是单值二叉树
        return false;
    else//如果x没有改变那么就是单值二叉树
        return true;
}

---

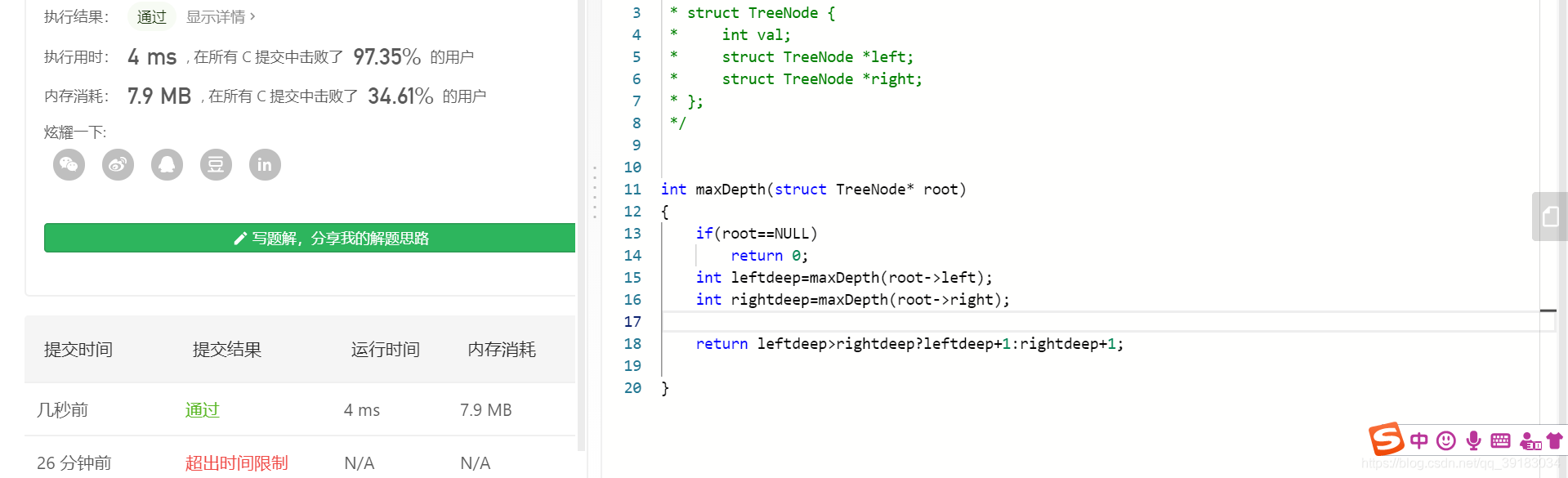
二叉树最大深度

题目

解法
这是一个递归问题，划分子问题即可。树的深度=左子树的深度和右子树深度大者取其并加1.。这里注意使用三目运算符时，不要重复递归，否则时间复杂度过高

int maxDepth(struct TreeNode* root)
{
    
    
    if(root==NULL)
        return 0;
    int leftdeep=maxDepth(root->left);
    int rightdeep=maxDepth(root->right);

    return leftdeep>rightdeep?leftdeep+1:rightdeep+1;
   
}

---

翻转二叉树

题目

解法
此题比较简单，只需递归，每次递归时交换根节点的两个孩子即可

struct TreeNode* invertTree(struct TreeNode* root)
{
    
    
    if(root != NULL)
    {
    
    
        struct TreeNode* cur=root->left;
        root->left=root->right;
        root->right=cur;

        invertTree(root->left);
        invertTree(root->right);
    }
    return root;
}

---

相同的树

题目

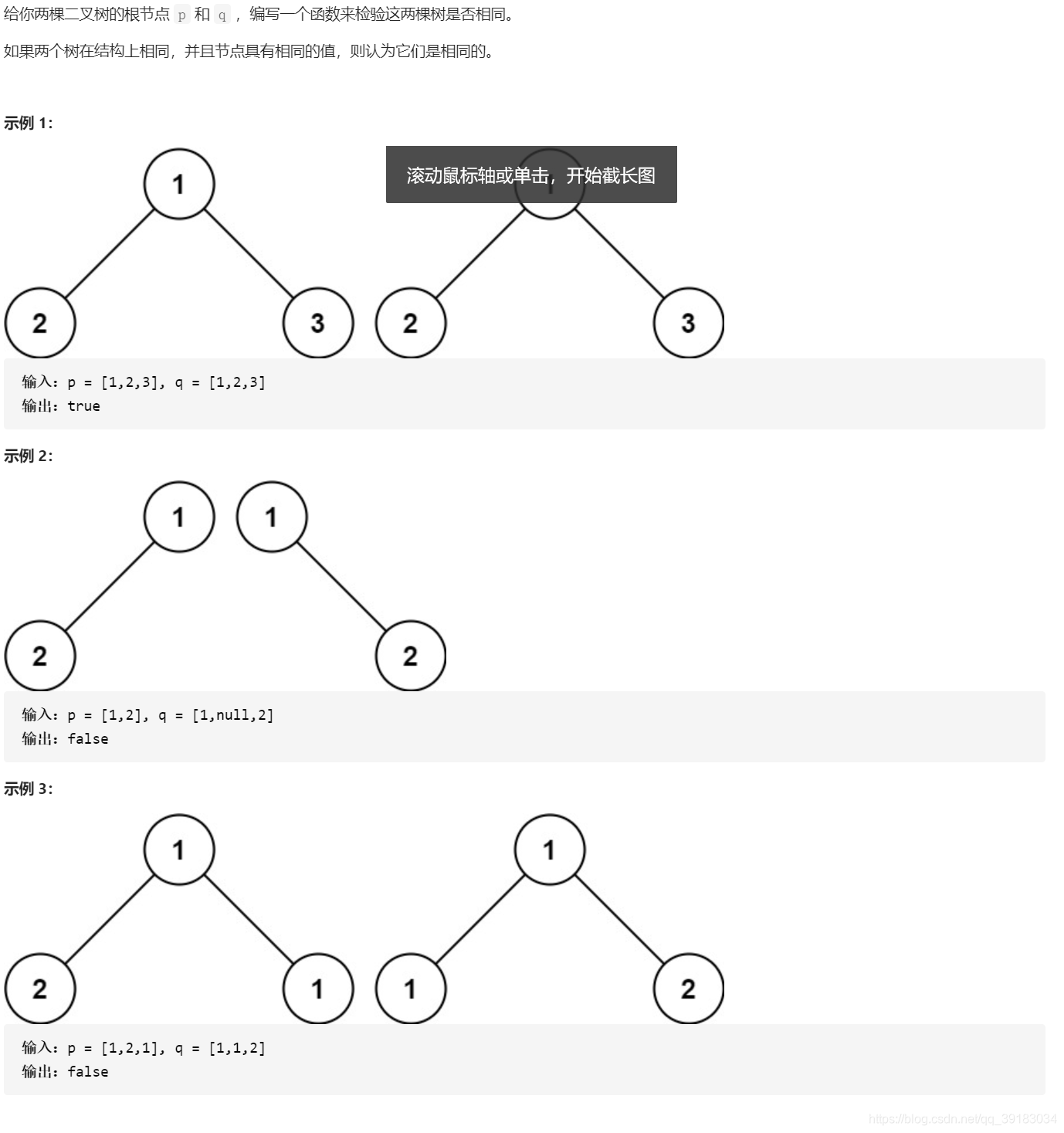
解法
此题也属于递归。如果结构相同同时值相同那么就去判断其子树（递归），注意中间会有一种特殊情况，如果p和q同时为NULL，这时的二叉树没有右子树，属于单链的二叉树

bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
    
    
    if((p&&q)&&(p->val==q->val))//这种情况相同，可以去判定子树
       return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
    else if(p==NULL&&q==NULL)//单链情况，也属于相同
        return true;
    else
        return false;
}

是否为子树

题目

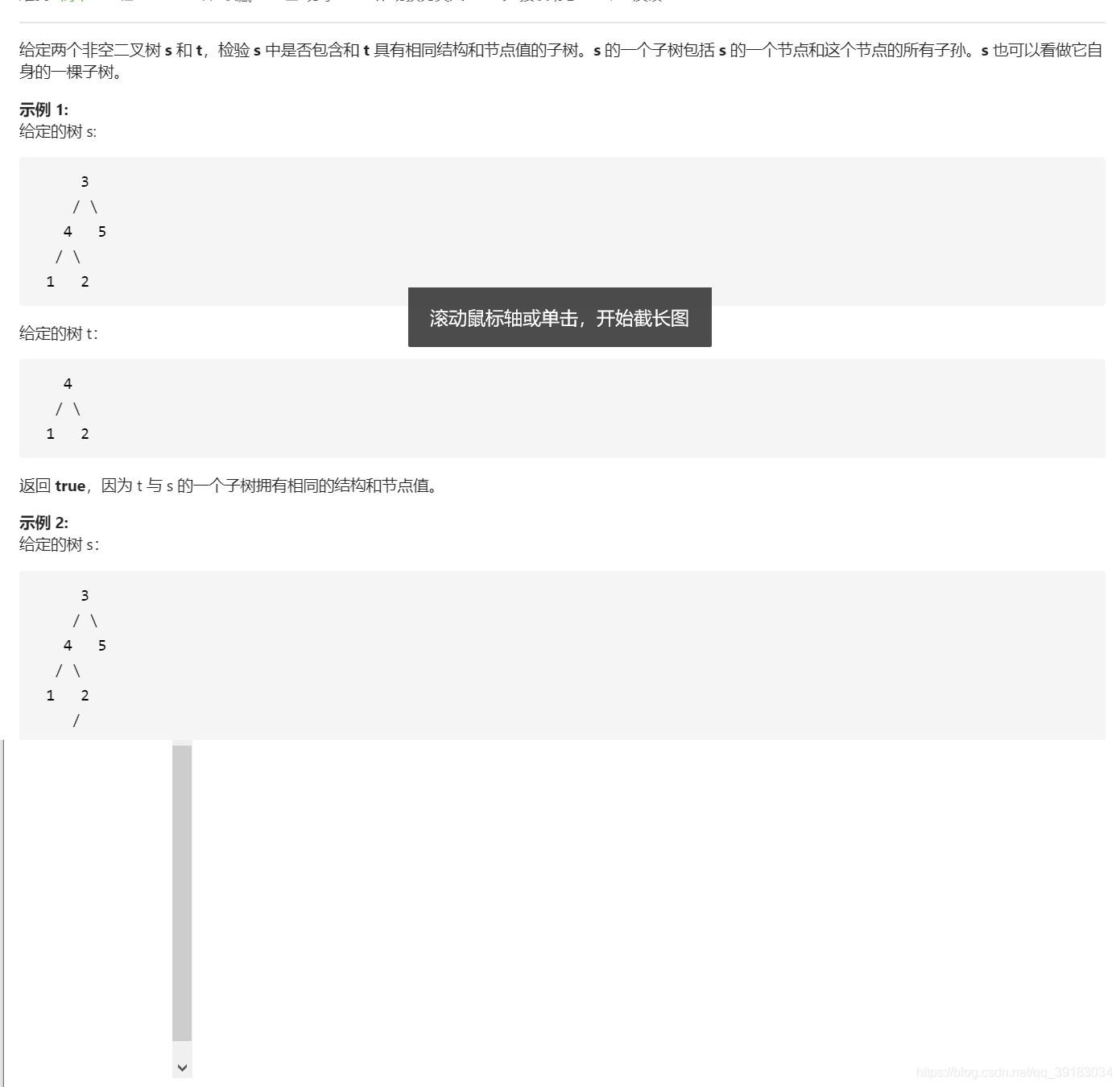
本题可以借助相同的树，如果某一时刻，根节点相同并且其子树也相同，那么就存在子树。注意后面递归时是“或”，因为如果左树没有子树，还要去右树找。

bool isSameTree(struct TreeNode* p, struct TreeNode* q)//判断是否为相同的树
{
    
    
    if((p==NULL&&q==NULL))
        return true;
    if((p&&q)&&(p->val==q->val))//这种情况相同，可以去判定子树
       return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
    else
        return false;
}

bool isSubtree(struct TreeNode* s, struct TreeNode* t)
{
    
    
    if(s==NULL)//如果s是空树，false
        return false;
    else if(s->val==t->val && isSameTree(s,t))//如果s和t的根节点相同，并且他们的子树相同，true
        return true;
    else//否则再去s的左子树和右子树找寻
        return isSubtree(s->left,t)||isSubtree(s->right,t);


}

---

对称二叉树

题目

解法
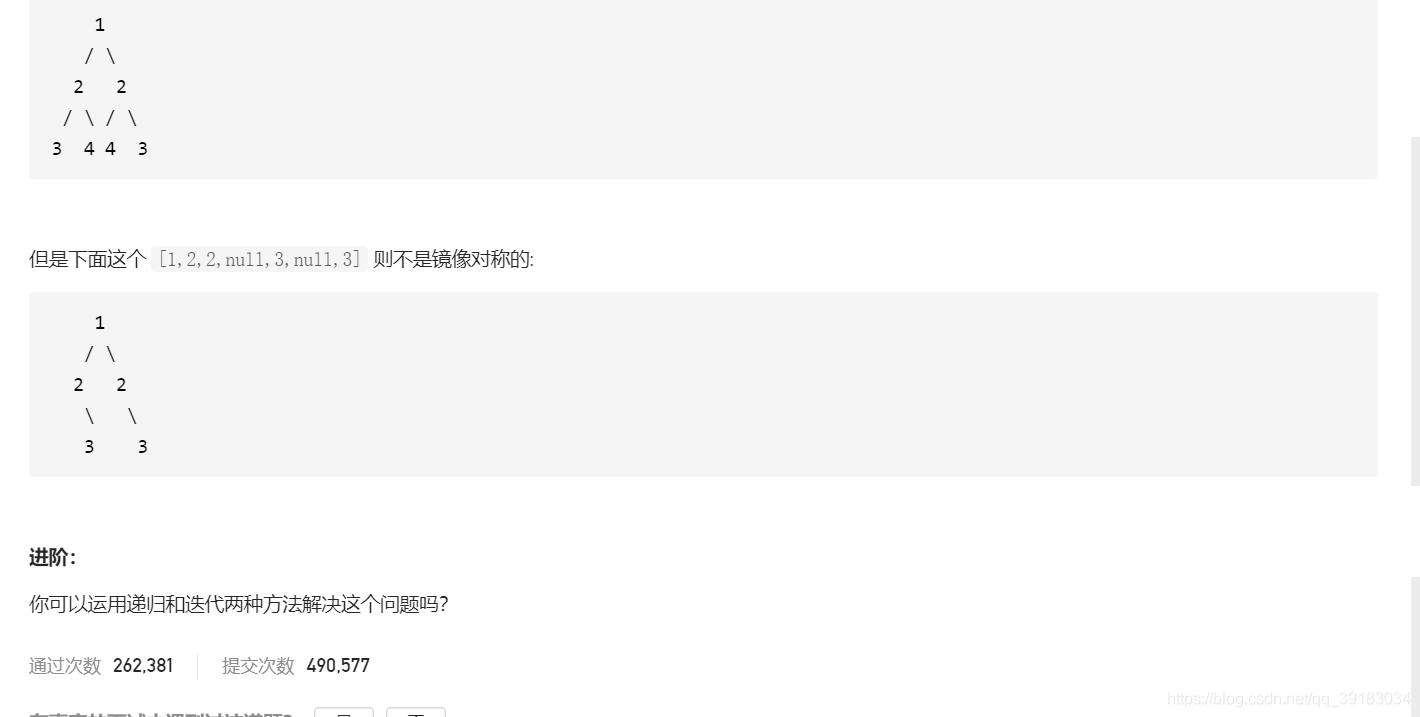
如果一棵树它的左子树和右子树是呈现镜像的，那么就是对称二叉树。
下面这棵树是一棵对称二叉树，是因为根节点的左孩子的左孩子和根节点的右孩子的右孩子是相同的，同时根节点的左孩子的右孩子和根节点的右孩子的左孩子是相同的。

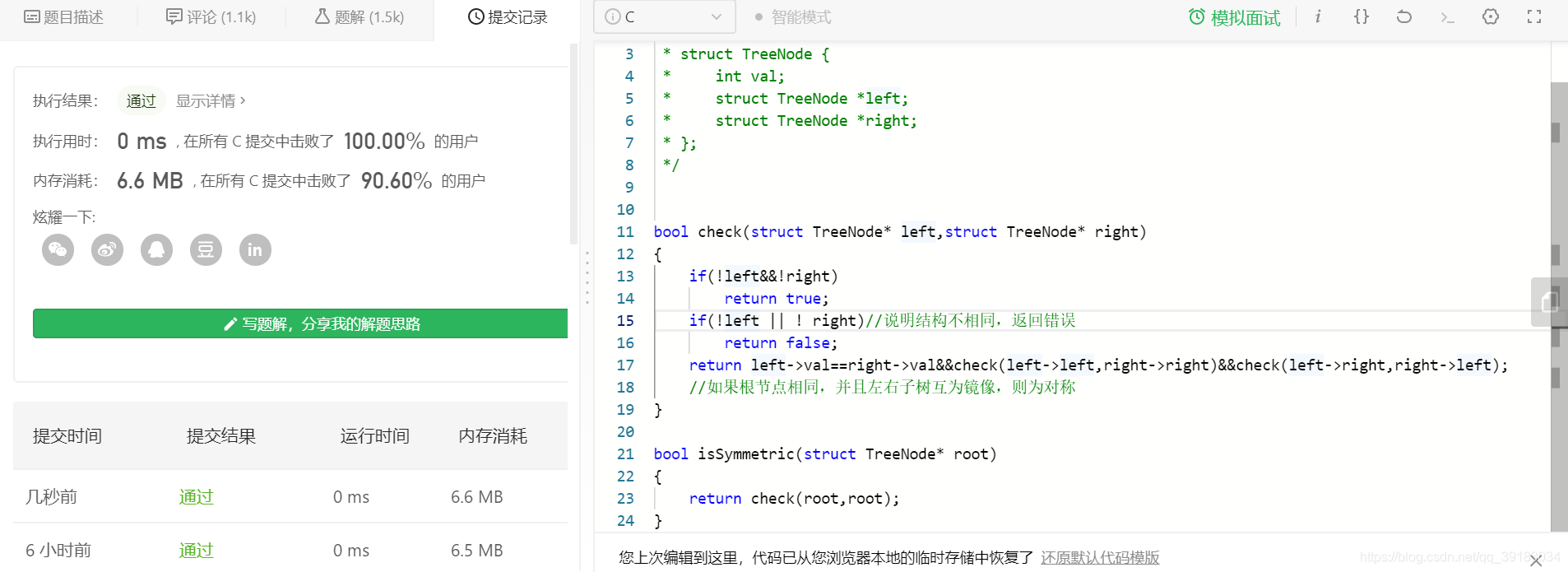
bool check(struct TreeNode* ll,struct TreeNode)
{
    
    
	if(ll==NULL && rr==NULL)//结构相同，切不存在返回true
		return true;
	else(ll==NULL || rr=NULL)//结构不同
		return false;
	return ll->val==rr->val && check(ll->left,rr->right) && check(ll->right,rr->left);//如果所对应结点相同，那么就去判断子树情况，
}

bool isSymmetric(struct TreeNode* root)
{
    
    
	return check(root,root);
	
}

---

平衡二叉树

题目

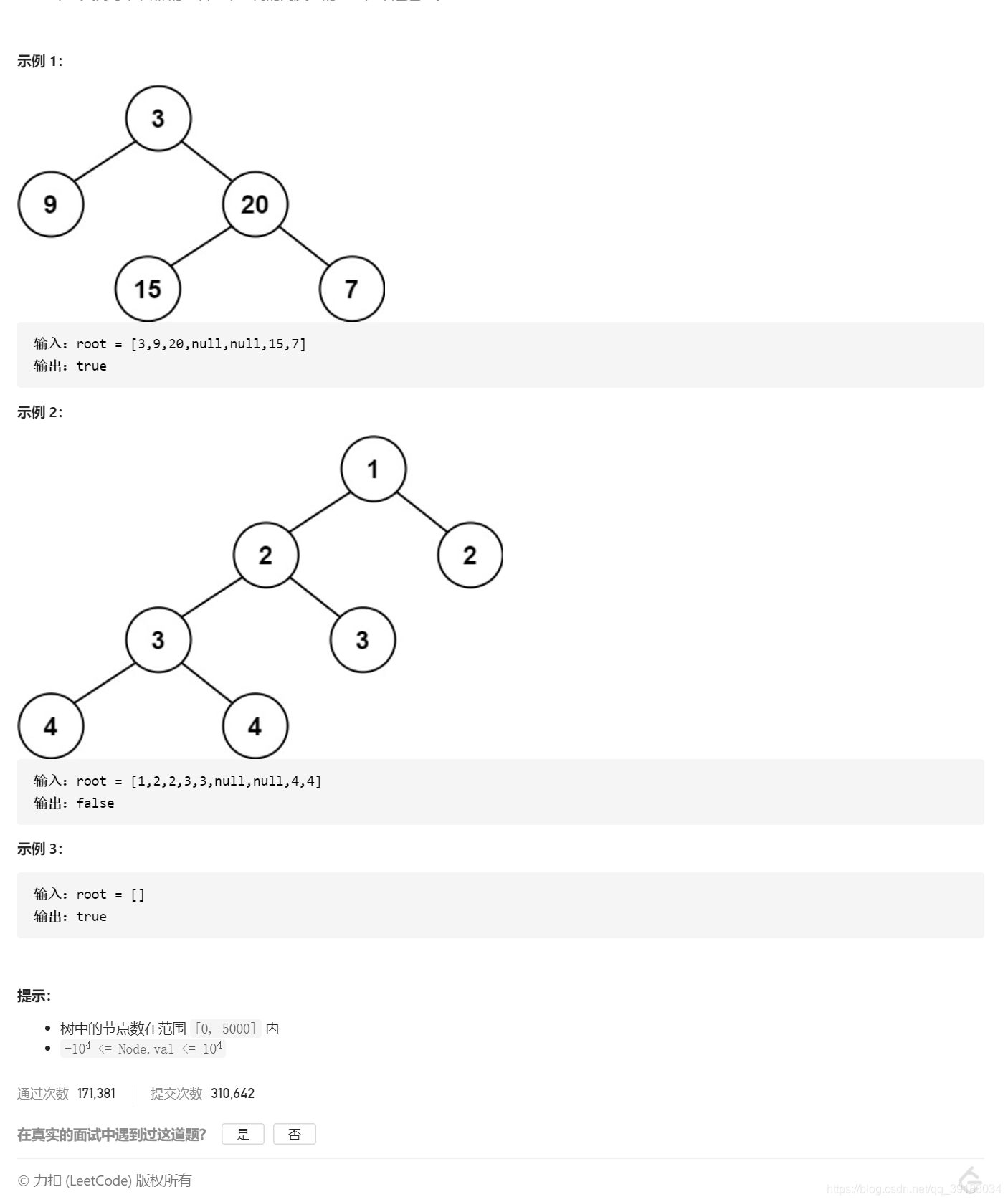
解法一

根据平衡二叉树的定义，如果某个结点的左子树之差大于1那么就不是空树，如果小于，则递归，看它左子树和右子树的情况

```c
 int depth(struct TreeNode* root)//求深度
{
    
    
    if(root==NULL)
        return 0;
    int leftdeep=depth(root->left);
    int rightdeep=depth(root->right);

    return leftdeep>rightdeep?leftdeep+1:rightdeep+1;
   
}

bool isBalanced(struct TreeNode* root)
{
    
    
   if(root==NULL)//空的是平衡
        return true;
    if(abs(depth(root->left)-depth(root->right))>1)//如果左右子树高度差大于1，则不是
    {
    
    
        return false;
    }
    return isBalanced(root->left)&& isBalanced(root->right);//如果不大于1，再看它的左右子树
}

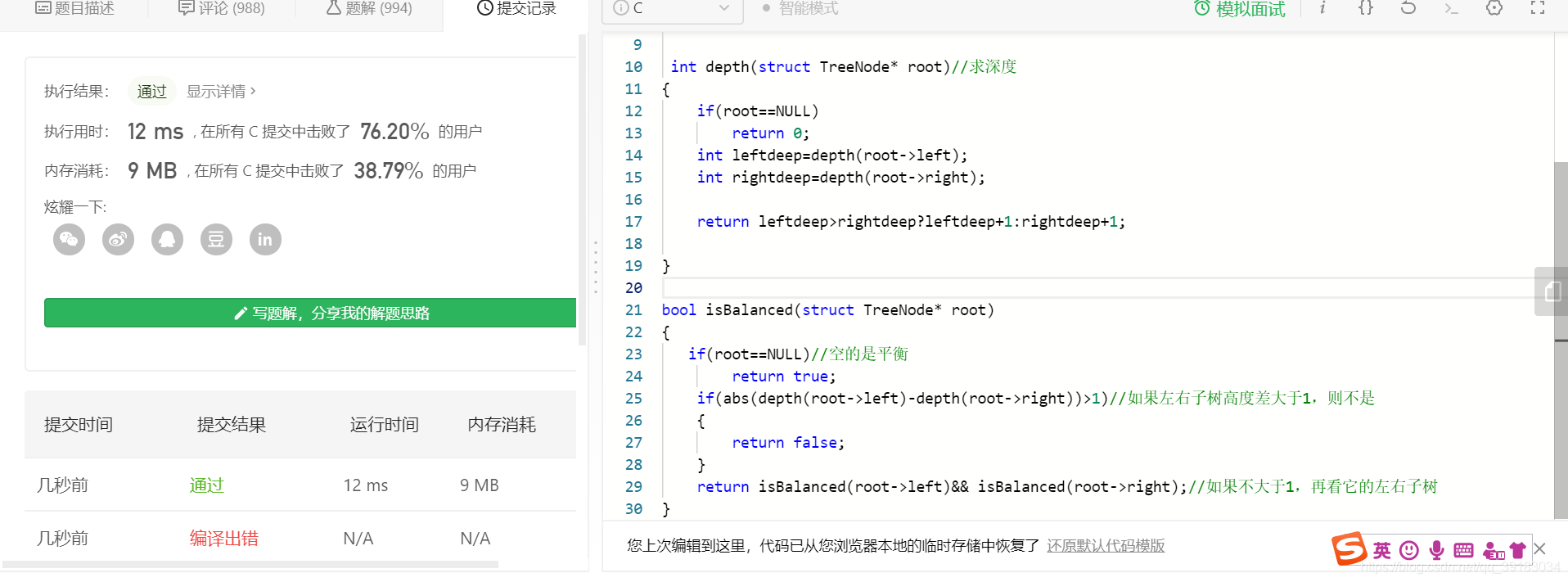
解法二
解法一本质采取的就是前序遍历，有一个非常大的缺点，就是高度在重复计算，根节点算了高度，用于判断根节点，然后第二层结点又去计算，从而使时间复杂度变大。
所以可以优化，才后序遍历，从最底层开始，如果这一层满足平衡，那么就给上一层返回true，同时返回自身高度

bool check(struct TtreeNode* root,int* depth)//depth用于向上高度
{
    
    
	if(root==NULL)//遇到空，满足条件，depth=0.同时向上一节点返回true，表明这个孩子满足情况
	{
    
    
		*depth=0;
		return true;
	}
	else//如果不是空,不能直接判断该结点（后序遍历）
	{
    
    
		int leftdepth=0;//不是空，先看左
		if(check(root->left,&leftdepth)==false)
			return false;//左子树不满足情况，剩下都不执行了
		int rightdepth=0;//左满足了，看下右
		if(check(root->right,&rightdepth)==false)
			return false;//右不满足，那么就不用判断本节点了


		//如果能走到这里，说明左右子树满足情况，看本节点
		if(abs(leftdepth-rightdepth)>1)
			return false;//本节点不满足情况
		//如果走到这里本节点也满足情况，向上一个接单返回高度和true
		*depth=leftdepth>rightdepth?leftdepth+1:rightdepth+1;
		return true;
	}
}
bool isBalanced(struct TreeNode* root)
{
    
    
    int depth=0;
    return check(root,&depth);

}

---

重建二叉树

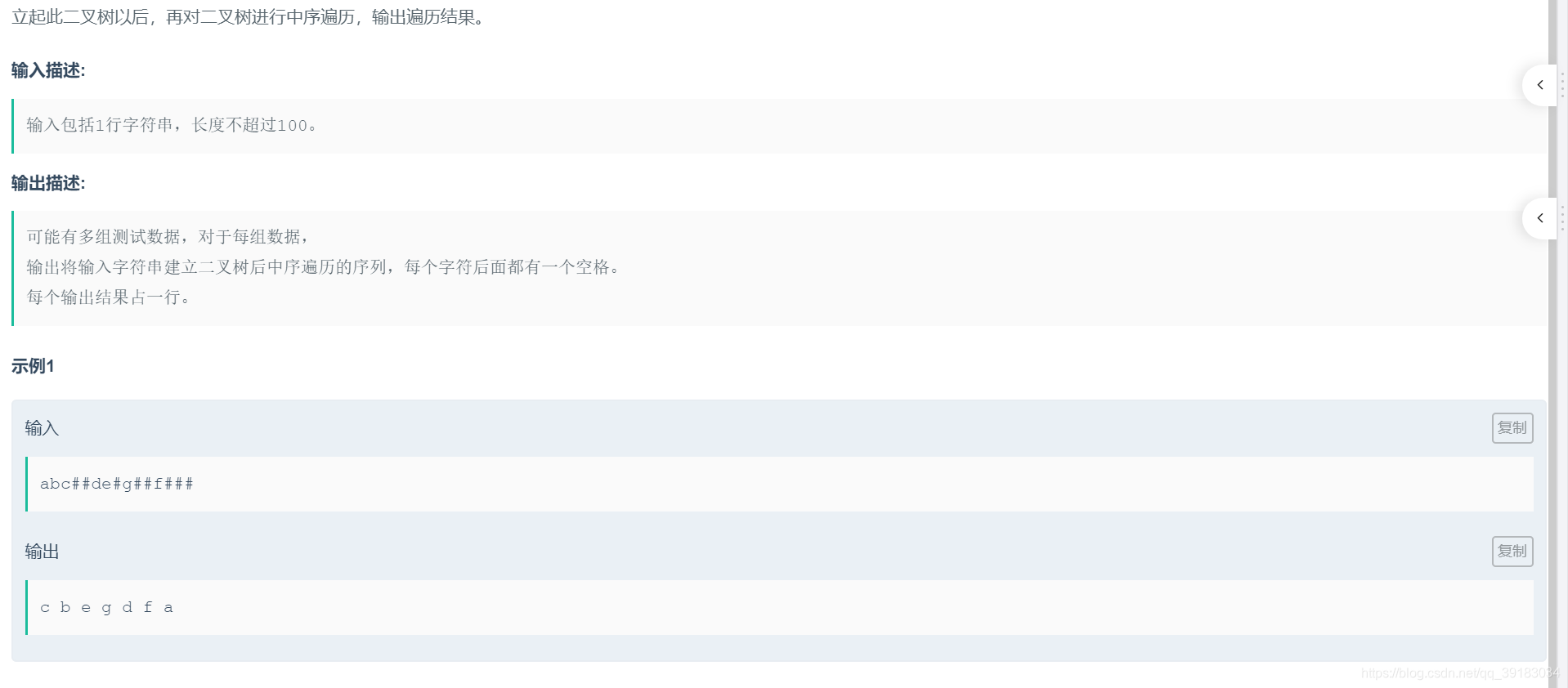
解法
实则是一个递归过程。每遇到一个新节点，就把它当做先序遍历的根节点进行构造，遇到#就为NULL，当一个结点的左右子树构造完成时，可以将该节点连接到上方结点，作为上一个结点孩子结点

#include <stdio.h>

typedef struct BTNode
{
    
    
    char val;
    struct BTNode* lchild;
    struct BTNode* rchild;
}BTNode;

BTNode* CreatTree(char* str,int* i)
{
    
    
    if(str[*i]=='#')
    {
    
    
        (*i)++;//注意不要忘记
        return NULL;
    }
    else
    {
    
    
        BTNode* root=(BTNode*)malloc(sizeof(BTNode));
        root->val=str[*i];
        (*i)++;
        root->lchild=CreatTree(str,i);
        root->rchild=CreatTree(str,i);
        
        return root;
    }
    
    
}

void Inorder(BTNode* root)
{
    
    
    if(root==NULL)
        return;
   Inorder(root->lchild);
   printf("%c ",root->val);
   Inorder(root->rchild);
    
}
int main()
{
    
    
    char str[100];
    scanf("%s",str);
    int i=0;
    Inorder(CreatTree(str,&i));
}