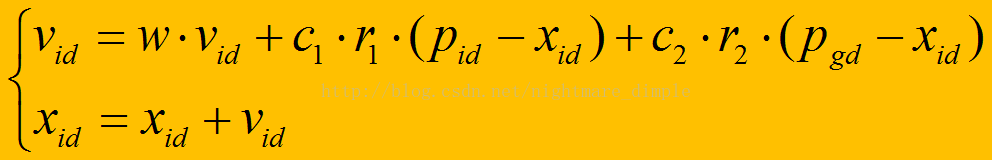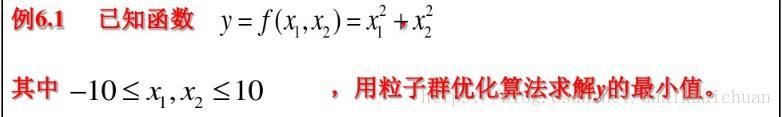理论基础
粒子群算法(Particle Swarm Optimization,POS)是一种常用的优化算法。
模拟了种群当中寻找食物的问题。
主要根据自身经验和 种群之间的交流来确定收敛的 速度和方向,寻找种群的极值和个体的极值。
PSO的优势:在于简单容易实现并且没有许多参数的调节。目前已被广泛应用于函数优化、神经网络训练、模糊系统控制以及其他遗传算法的应用领域。
对比之前的GA
POS主要在体现在它的记忆性和 种群之间的信息共享(双向)
其收敛速度快而令局部的最优解更加精确
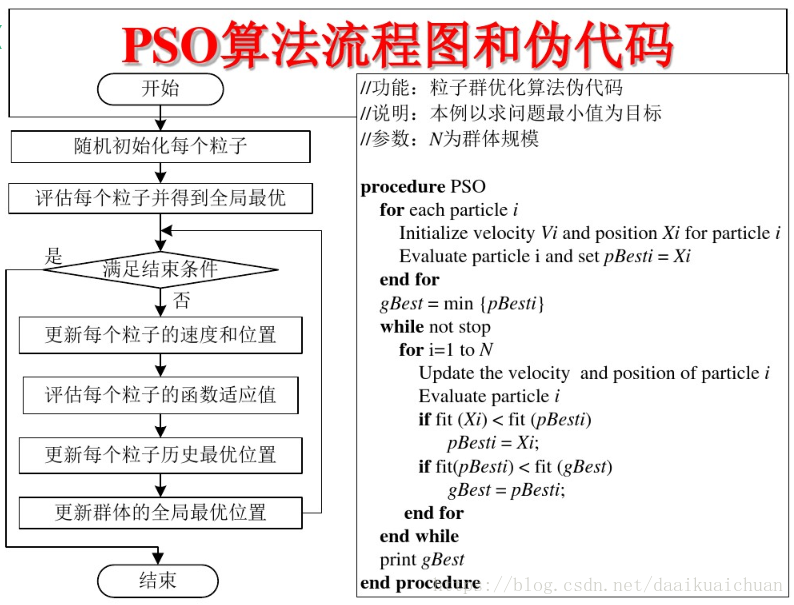
流程
速度公式
关于权值
算法流程图和伪代码实现
实例
一 .++实现
#include <iostream>
#include <vector>
#include <cmath>
#include <map>
#include <algorithm>
#include <random>
#include <ctime>
#include <Eigen/Dense>
using namespace Eigen;
using namespace std;
const int dim = 1;//维数
const int p_num = 10;//粒子数量
const int iters = 100;//迭代次数
const int inf = 999999;//极大值
const double pi = 3.1415;
//定义粒子的位置和速度的范围
const double v_max = 4;
const double v_min = -2;
const double pos_max = 2;
const double pos_min = -1;
//定义位置向量和速度向量
vector<double> pos;
vector<double> spd;
//定义粒子的历史最优位置和全局最优位置
vector<double> p_best;
double g_best;
//使用eigen库定义函数值矩阵和位置矩阵
Matrix<double, iters, p_num> f_test;
Matrix<double, iters, p_num> pos_mat;
//定义适应度函数
double fun_test(double x)
{
double res = x * x + 1;
return res;
}
//初始化粒子群的位置和速度
void init()
{
//矩阵中所有元素初始化为极大值
f_test.fill(inf);
pos_mat.fill(inf);
//生成范围随机数
static std::mt19937 rng;
static std::uniform_real_distribution<double> distribution1(-1, 2);
static std::uniform_real_distribution<double> distribution2(-2, 4);
for (int i = 0; i < p_num; ++i)
{
pos.push_back(distribution1(rng));
spd.push_back(distribution2(rng));
}
vector<double> vec;
for (int i = 0; i < p_num; ++i)
{
auto temp = fun_test(pos[i]);//计算函数值
//初始化函数值矩阵和位置矩阵
f_test(0, i) = temp;
pos_mat(0, i) = pos[i];
p_best.push_back(pos[i]);//初始化粒子的历史最优位置
}
std::ptrdiff_t minRow, minCol;
f_test.row(0).minCoeff(&minRow, &minCol);//返回函数值矩阵第一行中极小值对应的位置
g_best = pos_mat(minRow, minCol);//初始化全局最优位置
}
void PSO()
{
static std::mt19937 rng;
static std::uniform_real_distribution<double> distribution(0, 1);
for (int step = 1; step < iters; ++step)
{
for (int i = 0; i < p_num; ++i)
{
//更新速度向量和位置向量
spd[i] = 0.5 * spd[i] + 2 * distribution(rng) * (p_best[i] - pos[i]) +
2 * distribution(rng) * (g_best - pos[i]);
pos[i] = pos[i] + spd[i];
//如果越界则取边界值
if (spd[i] < -2 || spd[i] > 4)
spd[i] = 4;
if (pos[i] < -1 || pos[i] > 2)
pos[i] = -1;
//更新位置矩阵
pos_mat(step, i) = pos[i];
}
//更新函数值矩阵
for (int i = 0; i < p_num; ++i)
{
auto temp = fun_test(pos[i]);
f_test(step, i) = temp;
}
for (int i = 0; i < p_num; ++i)
{
MatrixXd temp_test;
temp_test = f_test.col(i);//取函数值矩阵的每一列
std::ptrdiff_t minRow, minCol;
temp_test.minCoeff(&minRow, &minCol);//获取每一列的极小值对应的位置
p_best[i] = pos_mat(minRow, i);//获取每一列的极小值,即每个粒子的历史最优位置
}
g_best = *min_element(p_best.begin(), p_best.end());//获取全局最优位置
}
cout << fun_test(g_best);
}
int main()
{
init();
PSO();
system("pause");
return 0;
}
二. Matlab实现寻找局部最大值
PSO多峰问题对于算法的检验效果最佳
算法的运行参数
PSO算法一个最大的优点是不需要调节太多的参数,但是算法中少数几个参数却直接影响着算法的性能和收敛性。
基本粒子群算法有下述7个运行参数需要提前设定:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SMicfahB-1598282969764)(C:\Users\Gary\AppData\Roaming\Typora\typora-user-images\image-20200824224637477.png)]
function [ xm,fv ] = PSO_lin(fitness,N,c1,c2,wmax,wmin,M,D)
format long ;
%给定初始化条件
% fitness:适应度函数
% N: 初始化种群数目
% c1: 个体最优化学习因子
% c2: 整体最优化学习因子
% wmax: 惯性权重最大值
% wmin: 惯性权重最小值
% M: 最大迭代次数
% D: 搜索空间的维数
% xm: 最佳个体
% fv: 适应度值
%初始化种群个体%
for i = 1:N
for j = 1:D
x(i,j) = randn ; %随机初始化位置
v(i,j) = randn ; %随机初始化速度
end
end
%先计算各个粒子的适应度,并初始化个体最优解pi和整体最优解pg %
%初始化pi %
for i = 1:N
p(i) = fitness(x(i,:)) ;
y(i,:) = x(i,:) ;
end
%初始化pg %
pg = x(N,:) ;
%得到初始的全局最优pg %
for i = 1:(N-1)
if fitness(x(i,:)) < fitness(pg)
pg = x(i,:) ;
end
end
%主循环函数,进行迭代,直到达到精度的要求 %
for t = 1:M
for i = 1:N %更新函数,其中v是速度向量,x为位置,i为迭代特征
w = wmax-(t-1)*(wmax-wmin)/(M-1)
v(i,:) = w*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(pg-x(i,:)) ;
x(i,:) = x(i,:)+v(i,:) ;
if fitness(x(i,:)) < p(i)
p(i) = fitness(x(i,:)) ;
y(i,:) = x(i,:) ;
end
if p(i) < fitness(pg)
pg = y(i,:) ;
end
end
Pbest(t) = fitness(pg) ;
end
%给出最后的计算结果 %
xm = pg' ;
fv = fitness(pg) ;
应用实例
自然选择
function [xm,fv]=PSO_nature(fitness,N,c1,c2,w,M,D)
% fitness:待优化的目标函数;
% N:粒子数目;
% c1:学习因子1;
% c2:学习因子2;
% w:惯性权重;
% M:最大迭代次数;
% D:自变量的个数;
% xm:目标函数取最小值时的自变量值;
% fv:目标函数的最小值。
format long;
for i=1:N
for j=1:D
x(i,j)=randn; %随机初始化位置
v(i,j)=randn; %随机初始化速度
end
end
for i=1:N
p(i)=fitness(x(i,:));
y(i,:)=x(i,:);
end
pg=x(N,:); %pg为全局最优
for i=1:(N-1)
if fitness(x(i,:))
pg=x(i,:);
end
end
for t=1:M
for i=1:N %速度、位移更新
v(i,:)=w*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(pg-x(i,:));
x(i,:)=x(i,:)+v(i,:);
fx(i)=fitness(x(i,:));
if fx(i)
p(i)=fx(i);
y(i,:)=x(i,:);
end
if p(i)
pg=y(i,:);
end
end
[sortf,sortx]=sort(fx); %将所有的粒子按适应值排序
exIndex=round((N-1)/2);
x(sortx((N-exIndex+1):N))=x(sortx(1:exIndex));%将最好的一半粒子的位置替换掉最差的一半
v(sortx((N-exIndex+1):N))=v(sortx(1:exIndex));%将最好的一半粒子的速度替换掉最差的一半
end
xm=pg';
fv=fitness(pg);
模拟退火
function [xm,fv]=PSO_lamda(fitness,N,c1,c2,lamda,M,D)
% fitness:待优化的目标函数;
% N:粒子数目;
% c1:学习因子1;
% c2:学习因子2;
% lamda:退火常数;
% M:最大迭代次数;
% D:自变量的个数;
% xm:目标函数取最小值时的自变量值;
% fv:目标函数的最小值。
format long;
for i=1:N
for j=1:D
x(i,j)=randn; %随机初始化位置
v(i,j)=randn; %随机初始化速度
end
end
for i=1:N
p(i)=fitness(x(i,:));
y(i,:)=x(i,:);
end
pg=x(N,:); %pg为全局最优
for i=1:(N-1)
if fitness(x(i,:))
pg=x(i,:);
end
end
T=-fitness(pg)/log(0.2); %初始温度
for t=1:M
groupFit=fitness(pg);
for i=1:N %当前温度下各个pi的适应值
Tfit(i)=exp(-(p(i)-groupFit)/T);
end
SumTfit=sum(Tfit);
Tfit=Tfit/SumTfit;
pBet=rand();
for i=1:N %用轮盘赌策略确定全局最优的某个替代值
ComFit(i)=sum(Tfit(1:i));
if pBet<=ComFit(i)
pg_plus=x(i,:);
break;
end
end
C=c1+c2;
ksi=2/abs(2-C-sqrt(C^2-4*C)); %速度压缩因子
for i=1:N
v(i,:)=ksi*(v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(pg_plus-x(i,:)));
x(i,:)=x(i,:)+v(i,:);
if fitness(x(i,:))
p(i)=fitness(x(i,:));
y(i,:)=x(i,:);
end
if p(i)
pg=y(i,:);
end
end
T=T*lamda;
Pbest(t) = fitness(pg) ;
end
xm=pg';
fv=fitness(pg);
工具箱
function z = pso_func(in)
n = size(in);
x = in(:,1);
y = in(:,2);
nx = n(1);
for i=1:nx
temp = 0.4*(x(i)-2)^2+0.3*(y(i)-4)^2-0.7;
z(i,:) = temp;
end
调用PSO算法的核心函数:pso_Trelea_vectorized
clear
clc
x_range = [-40,40];
y_range = [-40,40];
range = [x_range;y_range];
Max_V = 0.2*(range(:,2)-range(:,1));
n = 2;
pso_Trelea_vectorized('pso_func',n,Max_V,range)
执行即可得到答案。
在PSO算法函数pso_Trelea_vectorized173行中,PSO参数设置如下:
Pdef = [100 2000 24 2 2 0.9 0.4 1500 1e-25 250 NaN 0 1];
1
- 100:MATLAB命令窗口进行显示的间隔数
- 2000:最大迭代次数
- 24:初始化种子数,种子数越多,越有可能收敛到全局最优值,但算法收敛速度慢
- 2:算法的加速度参数,分别影响局部最优值和全局最优值,一般不需要修改
- 0.9和0.4为初始时刻和收敛时刻的加权值,一般不需要修改
- 1500:迭代次数超过此值时,加权值取其最小
- 1e-25:算法终止条件之一,当两次迭代中对应的种群最优值小于此阈值时,算法停止
- 250:算法终止条件之一,取NaN时表示为非约束下的优化问题(即没有附加约束方程)
- 0:制定采用何种PSO类型,0表示通常的PSO算法
- 1:说明是否指定种子,0表示随机产生种子,1表示用户自行产生种子
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-b3NwkpkZ-1598282969765)(C:\Users\Gary\AppData\Roaming\Typora\typora-user-images\image-20200824232423843.png)]
function main()
clc;clear all;close all;
tic; %程序运行计时
E0=0.001; %允许误差
MaxNum=100; %粒子最大迭代次数
narvs=1; %目标函数的自变量个数
particlesize=30; %粒子群规模
c1=2; %每个粒子的个体学习因子,也称为加速常数
c2=2; %每个粒子的社会学习因子,也称为加速常数
w=0.6; %惯性因子
vmax=0.8; %粒子的最大飞翔速度
x=-5+10*rand(particlesize,narvs); %粒子所在的位置
v=2*rand(particlesize,narvs); %粒子的飞翔速度
%用inline定义适应度函数以便将子函数文件与主程序文件放在一起,
%目标函数是:y=1+(2.1*(1-x+2*x.^2).*exp(-x.^2/2))
%inline命令定义适应度函数如下:
fitness=inline('1/(1+(2.1*(1-x+2*x.^2).*exp(-x.^2/2)))','x');
%inline定义的适应度函数会使程序运行速度大大降低
for i=1:particlesize
for j=1:narvs
f(i)=fitness(x(i,j));
end
end
personalbest_x=x;
personalbest_faval=f;
[globalbest_faval i]=min(personalbest_faval);
globalbest_x=personalbest_x(i,:);
k=1;
while k<=MaxNum
for i=1:particlesize
for j=1:narvs
f(i)=fitness(x(i,j));
end
if f(i)<personalbest_faval(i) %判断当前位置是否是历史上最佳位置
personalbest_faval(i)=f(i);
personalbest_x(i,:)=x(i,:);
end
end
[globalbest_faval i]=min(personalbest_faval);
globalbest_x=personalbest_x(i,:);
for i=1:particlesize %更新粒子群里每个个体的最新位置
v(i,:)=w*v(i,:)+c1*rand*(personalbest_x(i,:)-x(i,:))...
+c2*rand*(globalbest_x-x(i,:));
for j=1:narvs %判断粒子的飞翔速度是否超过了最大飞翔速度
if v(i,j)>vmax;
v(i,j)=vmax;
elseif v(i,j)<-vmax;
v(i,j)=-vmax;
end
end
x(i,:)=x(i,:)+v(i,:);
end
if abs(globalbest_faval)<E0,break,end
k=k+1;
end
Value1=1/globalbest_faval-1; Value1=num2str(Value1);
% strcat指令可以实现字符的组合输出
disp(strcat('the maximum value','=',Value1));
%输出最大值所在的横坐标位置
Value2=globalbest_x; Value2=num2str(Value2);
disp(strcat('the corresponding coordinate','=',Value2));
x=-5:0.01:5;
y=2.1*(1-x+2*x.^2).*exp(-x.^2/2);
plot(x,y,'m-','linewidth',3);
hold on;
plot(globalbest_x,1/globalbest_faval-1,'kp','linewidth',4);
legend('目标函数','搜索到的最大值');xlabel('x');ylabel('y');grid on;toc;
PSO与BP神经网络
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qnZJRIL9-1598282969766)(C:\Users\Gary\AppData\Roaming\Typora\typora-user-images\image-20200824232555177.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UOi6RHWC-1598282969767)(C:\Users\Gary\AppData\Roaming\Typora\typora-user-images\image-20200824232620315.png)]
function main
clc;clear all;close all;
MaxRunningTime=1; %该参数是为了使网络集成,重复训练MaxRunningTime次
HiddenUnitNum=12;
rand('state',sum(100*clock));
TrainSamIn=-4:0.07:2.5;
TrainSamOut=1.1*(1-TrainSamIn+2*TrainSamIn.^2).*exp(-TrainSamIn.^2/2);
TestSamIn=2:0.04:3;
TestSamOut=1.1*(1-TestSamIn+2*TestSamIn.^2).*exp(-TestSamIn.^2/2);
[xxx,TrainSamNum]=size(TrainSamIn);
[xxx,TestSamNum]=size(TestSamIn);
% for HiddenUnitNum=3:MaxHiddenLayerNode %隐含层神经元的个数可以取逐渐增大的合理整数
fprintf('\n the hidden layer node');HiddenUnitNum
TrainNNOut=[];
TestNNOut=[];
for t=1:MaxRunningTime
fprintf('the current running times is');t
[NewW1,NewB1,NewW2,NewB2]=PSOTrain(TrainSamIn,TrainSamOut,HiddenUnitNum);
disp('PSO算法训练神经网络结束,BP算法接着训练网络……');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%BP算法参数初始化,注意与上面PSO参数一致
SamInNum=length(TrainSamIn);
TestSamNum=length(TestSamIn);
InDim=1;
OutDim=1;
%学习样本添加噪声
rand('state',sum(100*clock))
NoiseVar=0.01;
Noise=NoiseVar*randn(1,SamInNum);
SamIn=TrainSamIn;
SamOutNoNoise=TrainSamOut;
SamOut=SamOutNoNoise + Noise;
MaxEpochs=300;
lr=0.003;
E0=0.0001;
W1=NewW1;
B1=NewB1;
W2=NewW2';
B2=NewB2;
W1Ex=[W1 B1];
W2Ex=[W2 B2];
SamInEx=[SamIn' ones(SamInNum,1)]';
ErrHistory=[];
%网络参数初始化完毕
%给动画初始画图和构建动画框架和背景
HiddenOut=logsig(W1Ex*SamInEx);
HiddenOutEx=[HiddenOut' ones(SamInNum,1)]';
NetworkOut=W2Ex*HiddenOutEx;
Error=SamOut-NetworkOut;
%给误差的动画显示提供空矩阵和其维数
SSEINIT=zeros(1,MaxEpochs);
%这仅限于输出是一维的情况
SSE=sumsqr(Error);
%绘画动画显示的图形框架
figure(1);
rangecolour=linspace(0,1,MaxEpochs);
%采用分区画图,把两幅动画在一个figure中显示
%先画第一幅图形
subplot(2,1,1);
hold on
axis([1 SamInNum min(SamOut) max(SamOut)]);
hflash1=line(1:SamInNum,SamOut,'color',[rangecolour(1) 0 1-rangecolour(1)],...
'linestyle','-','linewidth',2,'marker','d',...
'markersize',2,'erasemode','none');
hflash2=line(1:SamInNum,NetworkOut,'color',[rangecolour(1) 0 1-rangecolour(1)],...
'linestyle','-','linewidth',2.5,'marker','h',...
'markersize',2.3,'erasemode','xor');
xlabel('训练样本的数目');
ylabel('样本的输出值或网络的输出值');
title('样本的输出值与网络的输出值动画显示','fontsize',13);
legend('样本的输出值','网络的输出值');
hold off
%再画第二幅图形
subplot(2,1,2);
hold on
axis([1 MaxEpochs -0.2*SSE SSE]);
hflash3=line(1:MaxEpochs,E0*ones(1,MaxEpochs),'color',...
[rangecolour(1) 0 1-rangecolour(1)],...
'linestyle','--','linewidth',2,'marker','h',...
'markersize',2,'erasemode','none');
hflash4=line(1,SSE,'color',...
[rangecolour(1) 0 1-rangecolour(1)],...
'linestyle','-','linewidth',2,'marker','*',...
'markersize',2,'erasemode','xor');
xlabel('网络训练次数');
ylabel('目标误差或网络输出误差');
title('目标误差与网络输出误差动画显示','fontsize',13);
legend('目标误差','网络输出误差');
hold off
for i=2:MaxEpochs
HiddenOut=logsig(W1Ex*SamInEx);
HiddenOutEx=[HiddenOut' ones(SamInNum,1)]';
NetworkOut=W2Ex*HiddenOutEx;
Error=SamOut-NetworkOut;
SSE=sumsqr(Error)
%让第二幅动画逐点显示
SSEINIT(:,i)=SSE;
%对于神经网络训练过程中发生震荡的瞬间图像将其显示出来
ErrHistory=[ErrHistory SSE];
SSEINIT(:,1);
SSEINIT(:,2);
SSEINIT2=SSEINIT(:,i);
SSEINIT1=SSEINIT(:,i-1);
if SSE<E0,break, end
Delta2=Error;
Delta1=W2'*Delta2.*HiddenOut.*(1-HiddenOut);
dW2Ex=Delta2*HiddenOutEx';
dW1Ex=Delta1*SamInEx';
W1Ex=W1Ex+lr*dW1Ex;
W2Ex=W2Ex+lr*dW2Ex;
W2=W2Ex(:,1:HiddenUnitNum);
if SSEINIT2>SSEINIT1
%如果网络学习时发生震荡,每10步显示一次
if mod(i,10)==0
Counter(i)=SSEINIT(:,i);
Len=size(Counter);
figure(Len(1,2));
subplot(2,1,1);
hold on
axis([1 SamInNum min(SamOut) max(SamOut)]);
hflash5=line(1:SamInNum,SamOut,'color',[rangecolour(1) 0 1-rangecolour(1)],...
'linestyle','-','linewidth',2,'marker','d',...
'markersize',2,'erasemode','none');
hflash6=line(1:SamInNum,NetworkOut,'color',[rangecolour(MaxEpochs) 0 1-rangecolour(MaxEpochs)],...
'linestyle','-','linewidth',2.5,'marker','h',...
'markersize',2.3,'erasemode','xor');
xlabel('训练样本的数目');
ylabel('样本的输出值或网络的输出值');
title('神经网络学习震荡时拟合曲线','fontsize',13);
legend('样本的输出值','网络的输出值');
hold off
%再画第二幅图形
subplot(2,1,2);
hold on
axis([1 MaxEpochs -2*SSEINIT(:,2) 2*SSEINIT(:,2)]);
hflash7=line(1:MaxEpochs,E0*ones(1,MaxEpochs),'color',...
[rangecolour(1) 0 1-rangecolour(1)],...
'linestyle','--','linewidth',2,'marker','h',...
'markersize',2,'erasemode','none');
hflash8=line(1:i,SSEINIT(:,1:i),'color',...
[rangecolour(1) 0 1-rangecolour(1)],...
'linestyle','-','linewidth',2,'marker','*',...
'markersize',2,'erasemode','xor');
xlabel('网络训练次数');
ylabel('目标误差或网络输出误差');
title('神经网络学习震荡时误差','fontsize',13);
legend('目标误差','网络输出误差');
hold off
end
end
%动画开始放映
set(hflash2,'XData',1:SamInNum,'YData',NetworkOut,'color',...
[rangecolour(MaxEpochs) 0 1-rangecolour(MaxEpochs)]);
set(hflash4,'XData',1:i,'YData',SSEINIT(:,1:i),...
'color',[rangecolour(MaxEpochs) 0 1-rangecolour(MaxEpochs)]);
drawnow;
end
W2=W2Ex(:,1:HiddenUnitNum);
W1=W1Ex(:,1:InDim);
B1=W1Ex(:,InDim+1);
B2=W2Ex(:,1+HiddenUnitNum);
TrainHiddenOut=logsig(W1*SamIn+repmat(B1,1,SamInNum));
TrainNNOut=W2*TrainHiddenOut+repmat(B2,1,SamInNum);
TestHiddenOut=logsig(W1*TestSamIn+repmat(B1,1,TestSamNum));
TestNNOut=W2*TestHiddenOut+repmat(B2,1,TestSamNum);
figure(MaxEpochs+1);
hold on;
grid;
h1=plot(SamIn,SamOut);
set(h1,'color','r','linestyle','-',...
'linewidth',2.5,'marker','p','markersize',5);
hold on
h2=plot(TestSamIn,TestSamOut);
set(h2,'color','g','linestyle','--',...
'linewidth',2.5,'marker','^','markersize',7);
h3=plot(SamIn,TrainNNOut);
set(h3,'color','c','linestyle','-.',...
'linewidth',2.5,'marker','o','markersize',5);
h4=plot(TestSamIn,TestNNOut);
set(h4,'color','m','linestyle',':',...
'linewidth',2.5,'marker','s','markersize',5);
xlabel('Input x','fontsize',13);ylabel('Output y','fontsize',13);
box on;axis tight;
%title('PSO-BP神经网络误差测试图');
legend('网络学习实际样本值','网络测试实际样本值',...
'网络学习网络输出值','网络测试网络输出值');
hold off;
end
% end
fidW1=fopen('d:\W1.txt','a+');fidB1=fopen('d:\B1.txt','a+');
fidW2=fopen('d:\W2.txt','a+');fidB2=fopen('d:\B2.txt','a+');
for i=1:length(W1)
fprintf(fidW1,'\n %6.5f',W1(i));
end
for i=1:length(B1)
fprintf(fidB1,'\n %6.5f',B1(i));
end
for i=1:length(W2)
fprintf(fidW2,'\n %6.5f',W2(i));
end
for i=1:length(B2)
fprintf(fidB2,'\n %6.5f',B2(i));
end
fclose(fidW1);fclose(fidB1);fclose(fidW2);fclose(fidB2);
function [NewW1,NewB1,NewW2,NewB2]=PSOTrain(SamIn,SamOut,HiddenUnitNum);
Maxgeneration=700;
E0=0.0001;
Xmin=-10;
Xmax=10;
Vmin=-5;
Vmax=5;
M=100;
c1=2.7;
c2=1.3;
w=0.9;
[R,SamNum]=size(SamIn);
[S2,SamNum]=size(SamOut);
generation=1;
Done=0;
Pb1=zeros(HiddenUnitNum,R+S2+1,M);
Pb2=zeros(S2,M);
Pg1=zeros(HiddenUnitNum,R+S2+1);
Pg2=zeros(S2,1);
E=zeros(size(SamOut));
rand('state',sum(100*clock));
startP1=rand(HiddenUnitNum,R+S2+1,M)-0.5;
startP2=rand(S2,M)-0.5;
startV1=rand(HiddenUnitNum,R+S2+1,M)-0.5;
startV2=rand(S2,M)-0.5;
endP1=zeros(HiddenUnitNum,R+S2+1,M);
endP2=zeros(S2,M);
endV1=zeros(HiddenUnitNum,R+S2+1,M);
endV2=zeros(S2,M);
startE=zeros(1,M);
endE=zeros(1,M);
for i=1:M
W1=startP1(1:HiddenUnitNum,1:R,i);
W2=startP1(1:HiddenUnitNum,R+1:R+S2,i);
B1=startP1(1:HiddenUnitNum,R+S2+1,i);
B2=startP2(1:S2,i);
for q=1:SamNum
TempOut=logsig(W1*SamIn(:,q)+B1);
NetworkOut(1,q)=W2'*TempOut+B2;
end
E=NetworkOut-SamOut;
startE(1,i)=sumsqr(E)/(SamNum*S2);
Pb1(:,:,i)=startP1(:,:,i);
Pb2(:,i)=startP2(:,i);
end
[val,position]=min(startE(1,:));
Pg1=startP1(:,:,position);
Pg2=startP2(:,position);
Pgvalue=val;
Pgvalue_last=Pgvalue;
while(~Done)
for num=1:M
endV1(:,:,num)=w*startV1(:,:,num)+c1*rand*(Pb1(:,:,num)-startP1(:,:,num))+c2*rand*(Pg1-startP1(:,:,num));
endV2(:,num)=w*startV2(:,num)+c1*rand*(Pb2(:,num)-startP2(:,num))+c2*rand*(Pg2-startP2(:,num));
for i=1:HiddenUnitNum
for j=1:(R+S2+1)
endV1(i,j,num)=endV1(i,j,num);
if endV1(i,j,num)>Vmax
endV1(i,j,num)=Vmax;
elseif endV1(i,j,num)<Vmin
endV1(i,j,num)=Vmin;
end
end
end
for s2=1:S2
endV2(s2,num)=endV2(s2,num);
if endV2(s2,num)>Vmax
endV2(s2,num)=Vmax;
elseif endV2(s2,num)<Vmin
endV2(s2,num)=Vmin;
end
end
endP1(:,:,num)=startP1(:,:,num)+endV1(:,:,num);
endP2(:,num)=startP2(:,num)+endV2(:,num);
for i=1:HiddenUnitNum
for j=1:(R+S2+1)
if endP1(i,j,num)>Xmax
endP1(i,j,num)=Xmax;
elseif endP1(i,j,num)<Xmin
endP1(i,j,num)=Xmin;
end
end
end
for s2=1:S2
if endP2(s2,num)>Xmax
endP2(s2,num)=Xmax;
elseif endP2(s2,num)<Xmin
endP2(s2,num)=Xmin;
end
end
W1=endP1(1:HiddenUnitNum,1:R,num);
W2=endP1(1:HiddenUnitNum,R+1:R+S2,num);
B1=endP1(1:HiddenUnitNum,R+S2+1,num);
B2=endP2(1:S2,num);
for q=1:SamNum
TempOut=logsig(W1*SamIn(:,q)+B1);
NetworkOut(1,q)=W2'*TempOut+B2;
end
E=NetworkOut-SamOut;
SSE=sumsqr(E) %便于在命令窗口观察网络误差的变化情况
endE(1,num)=sumsqr(E)/(SamNum*S2);
if endE(1,num)<startE(1,num)
Pb1(:,:,num)=endP1(:,:,num);
Pb2(:,num)=endP2(:,num);
startE(1,num)=endE(1,num);
end
end
w=0.9-(0.5/Maxgeneration)*generation;
[value,position]=min(startE(1,:));
if value<Pgvalue
Pg1=Pb1(:,:,position);
Pg2=Pb2(:,position);
Pgvalue=value;
end
if (generation>=Maxgeneration)
Done=1;
end
if Pgvalue<E0
Done=1;
end
startP1=endP1;
startP2=endP2;
startV1=endV1;
startV2=endV2;
startE=endE;
generation=generation+1;
end
W1=Pg1(1:HiddenUnitNum,1:R);
W2=Pg1(1:HiddenUnitNum,R+1:R+S2);
B1=Pg1(1:HiddenUnitNum,R+S2+1);
B2=Pg2(:,1);
NewW1=W1;
NewW2=W2;
NewB1=B1;
NewB2=B2;