PLL,Phase Locked Loop,锁相环,它的作用是得出正弦波的相位和角速度(区别于芯片硬件上的倍频器)。
为弄清PLL的原理,先来点先导知识:
旋转矢量与三角函数的关系
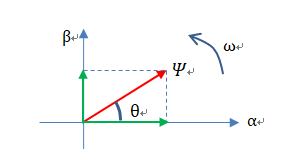
在直角坐标系αβ中有一个旋转矢量![]() (模值为
(模值为![]() ),在直角坐标系中以速度ω(rad/s)绕中心点逆时针旋转,其在两坐标轴的投影分别为:
),在直角坐标系中以速度ω(rad/s)绕中心点逆时针旋转,其在两坐标轴的投影分别为:
①α坐标轴
![]()
②β坐标轴
![]()
下面这个PLL环的作用就是求出旋转矢量Ψ的速度ω和角度θ,推导如下:

上图中比较点的输出

其中,θ为矢量的实际角度,![]() 为矢量的估计角度,PLL的目的就是让这两个角度相等。
为矢量的估计角度,PLL的目的就是让这两个角度相等。
有这么个规律最为关键和有趣:
在角度θ(弧度制)很小的条件下,存在
sinθ ≈ θ
为了直观说明,我用Matlab画了一个图,如下所示:

我把m语言脚本也贴出来:
i = 0:0.01:0.5;
y = sin(i);
plot(i,y,'r');
hold on
plot(i,i,'b');
xlabel("弧度角度");
legend("sinθ","θ(弧度)");于是在直角坐标系中,当角度差很小时就有
![]()
上面的PLL示意图就可以惊奇地等效为

根据框图,得到开环传递函数

闭环传递函数为

这是一个2型系统,对于斜坡输入(假设角度随时间线性增大),稳态误差为0。
为了验证上面推导的正确性,我在Simulink中搭建了一个PLL模型,如下图所示:

在调试过程中发现,随着验证的矢量旋转速度越快,PI参数中的KP/KI也要相应增大,不然上升时间太长,系统快速性指标会比较差。
仿真结果:

可以看出,模型完成了锁相的目的,推导得到验证。