冒泡排序，选择排序，插入排序，希尔排序，快速排序，归并排序

冒泡排序

时间复杂度：o（n方）
空间复杂度为 0
有人会说这个空间复杂度能降到0，因为空间复杂度主要是看使用的辅助内存，如果没有辅助内存变量，那么可以说空间复杂度为0；所以该算法中空间复杂度一般是看交换元素时所使用的辅助空间
稳定性：稳定

package CL7_class;

/**
 * @author: 贾兴伟
 * @date: Created in 14:49 2020/9/29
 */
public class maopao {
    
    
    public static void main(String[] args) {
    
    
        double[] score = {
    
    1,5,3,6,4,8,2,10,11,17.2,13.4,7.6};
        double[] scored = sortd(score);
        for(double value:scored){
    
    
            System.out.print(value+"  ");
        }
    }
    public static double[] sortd(double[] score){
    
    
        int node = 1;
        //flag的作用是判断序列是否已经排好，若flag没有被++说明已经排好直接返回。
        for(int i =0;i<score.length;i++){
    
    
            int flag = 0;
            for(int j =0;j<score.length-node;j++){
    
    
                if(score[j]>score[j+1]){
    
    
                    double a = score[j];
                    score[j]=score[j+1];
                    score[j+1]=a;
                    flag++;
                }
            }
            if(flag==0){
    
    
                return score;
            }
            node ++;
        }
        return score;
    }
}

选择排序

时间复杂度：o（n方）其实可以理解为（n/2）方
空间复杂度：0
稳定性：不稳定

package Sort;

/**
 * @author: 贾兴伟
 * @date: Created in 23:20 2020/11/30
 */
public class Select_Sort {
    
    
    public static void show(int array[]){
    
    
        for(int i=0;i<array.length;i++){
    
    
            System.out.print(array[i]);
        }
        System.out.println(" ");
    }
    public static void selectSort(int array[]){
    
    
        if(array==null||array.length==0){
    
    
            return;
        }
        for (int i =0;i<array.length/2;i++){
    
    
            //两个设置成i没有关系，在对比的时候和最大值和最后一个比就好了
            int minindex =i;
            int maxindex =i;
            //循环里面只找最大最小元素的下标，循环出了以后再换。
            for (int j=i+1;j<=array.length-i-1;j++){
    
    
                if(array[j]<array[minindex]){
    
    
                    minindex = j;
                    continue;
                }
                if(array[j]>array[maxindex]){
    
    
                    maxindex = j;
                }
            }
            if(minindex!=i){
    
    
                int mid = array[i];
                array[i]=array[minindex];
                array[minindex]= mid;
            }
            //如果最大的元素下标是i，上一步交换了min和i的值，
            //max应该是min的下标
            if(maxindex==i){
    
    
                array[array.length-1-i]=array[minindex];
            }
            if(maxindex!=i){
    
    
                int mid = array[array.length-1-i];
                array[array.length-1-i]=array[maxindex];
                array[maxindex]= mid;
            }
        }

    }
    public static void main(String[] args) {
    
    
        int[] arr1 =new int[]{
    
    8,5,4,9,7,2,1,5,6,4};
        int[] arr2 =new int[]{
    
    2,8,4,6,8,7,2,6};
        selectSort(arr1);
        selectSort(arr2);
        show(arr1);
        show(arr2);
    }
}

插入排序

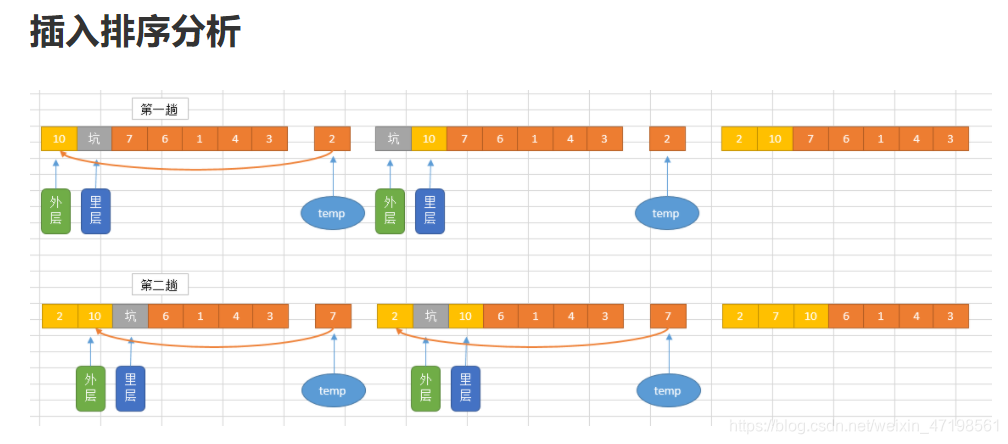
时间复杂度 O(N^2)
空间复杂度O(1)
//稳定
特点：越有序越快

public class InsertSort {
    
    
    public static void show(int array[]){
    
    
        for(int i=0;i<array.length;i++){
    
    
            System.out.print(array[i]);
        }
        System.out.println(" ");
    }
    public static void insertSort(int[] array){
    
    
        if(array == null || array.length == 0){
    
    
            return;
        }
        //时间复杂度 O(N^2) 空间复杂度O(1)
        //稳定
        for(int i=0; i<array.length; i++){
    
    
            //遍历每个i，arrar[i]就是每次需要往里插的牌。
            int tmp = array[i]; //要插的牌先存储起来
            int j = 0;
            //j从0到i-1就是之前已经插好的牌，i越往后，说明前面插好的牌越来越多。
            for(; j<=i-1; j++){
    
    
                //找到需要插得位置然后停下来
                if(array[j] > tmp){
    
    
                    break;
                }
            }
            //将j ~ i-1的牌逆序往后挪一位，i被覆盖掉
            for(int k=i; k>j; k--){
    
    
                array[k] = array[k-1];
            }
            //插牌
            array[j] = tmp;
        }
    }
    public static void main(String[] args) {
    
    
        int[] arr1 =new int[]{
    
    8,5,4,9,7,2,1,5,6,4};
        int[] arr2 =new int[]{
    
    2,8,4,6,8,7,2,6};
        int[] arr3 =new int[]{
    
    5,7,9,4,5,7,5,6,3,1,7,2,8,4};
        insertSort(arr1);
        insertSort(arr2);
        insertSort(arr3);
        show(arr1);
        show(arr2);
        show(arr3);
    }
}

希尔排序

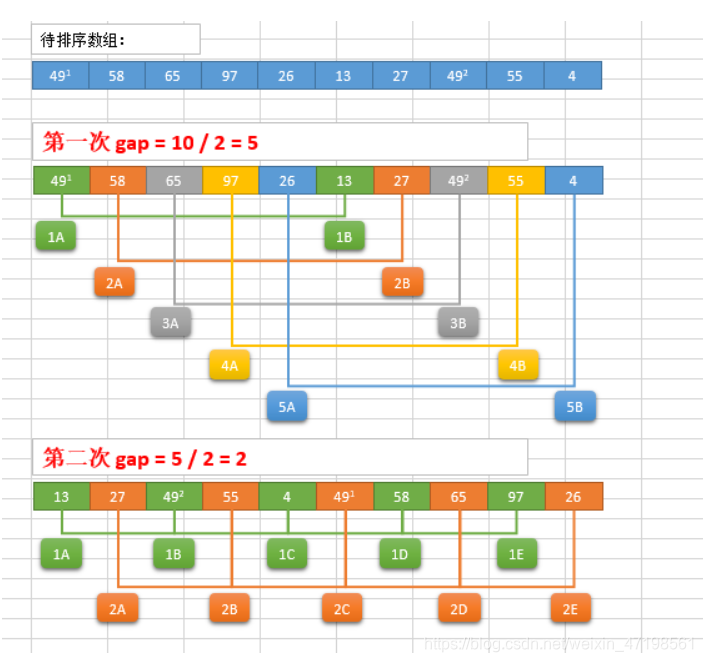
public class ShellSort {
    
    
    public static void shellSort(int[] array, int gap){
    
    
        //i从gap开始，因为前面只有一个不需要排序
        for(int i=gap; i<array.length; i++){
    
    
            int tmp = array[i];
            //在组内从后往前找比tmp小的数据
            int j;
            //从I的前一位即i-gap开始倒着来，一直到0
            for(j=i-gap; j>=0; j-=gap){
    
    
                //如果找到了跳出去，因为没找到前都把后面的挪过了
                if(array[j] <= tmp){
    
    
                    break;
                }else{
    
    
                    //每找一个元素，如果不是就直接往后挪
                    array[j+gap] = array[j];
                }
            }
            //出来直接放到j的后一位
            array[j+gap] = tmp;
        }
    }
    public static void shell(int[] array){
    
    
        if(array == null || array.length == 0){
    
    
            return;
        }
        //跳跃式分组
        int[] gap = {
    
    5,3,2,1};
        for(int i=0; i<gap.length; i++){
    
    
            shellSort(array, gap[i]);
        }
    }
    public static void main(String[] args) {
    
    
        int[] array = {
    
    4,8,4,5,8,2,6,8,1,3,8,5,3,7,2,9,5,2,7,6,5,5,7,1,3,2,1,9,8,7};
        shell(array);
        System.out.println(Arrays.toString(array));
    }

快速排序

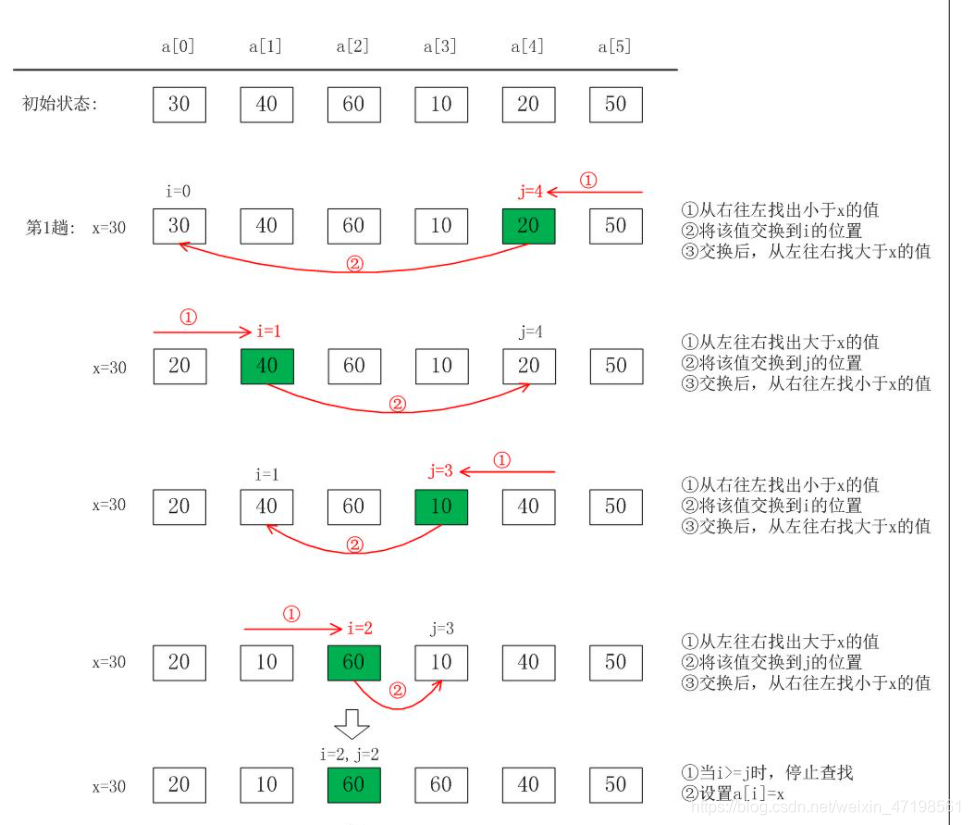
package Sort;

import java.util.Arrays;

/**
 * @author: 贾兴伟
 * @date: Created in 18:24 2020/12/2
 */
public class FastSort {
    
    
    //每次分1/2，最后分成一个。即（1/2）的X方 =1/n。 求X 即log2n
    //时间复杂度 O(N * log2 N) 空间复杂度 递归依赖于栈 O(log2 N)
    //不稳定
    public static int partition(int[] array, int start, int end){
    
    
        //O(log2 N)
        //完成一次划分的过程
        int mar = array[start];
        //一次划分的循环过程
        while(start < end){
    
    
            //从后往前找比基准小的元素
            while(start < end && array[end] >= mar){
    
    
                //1 2 3 4
                end--;
            }
            //跳出上面while循环
            //start == end 基准的右边都比大了
            if(start == end){
    
    
                break;
            }
            //array[end] < mar 此时end指向的元素就是所要找的小于基准的元素
            array[start] = array[end];
            //从前往后找比基准大的元素
            while(start < end && array[start] <= mar){
    
    
                start++;
            }
            //跳出上面while循环
            //start == end 基准的左边都比小了
            if(start == end){
    
    
                break;
            }
            //array[start] > mar 此时start指向的元素就是所要找的比基准大的元素
            array[end] = array[start];
        }
        array[start] = mar;
        return start;
    }

    public static void quick(int[] array, int start, int end){
    
    
        if(start >= end){
    
    
            return;
        }
        //第一次划分
        int mid = partition(array, start, end);

        //左边继续划分，因为start都是从0开始的，左边只有一个的时候就不需要分了，
        //左边只有一个的时候start是0，mid是1，所以start+1<mid的时候说明左边大于一个。
        //或者理解为mid-1>start所以mid>start+1
        if(mid > start+1){
    
    
            quick(array, start, mid-1);
        }
        //右边继续划分
        if(mid < end-1){
    
    
            quick(array, mid+1, end);
        }
    }

    public static void quickSort(int[] array){
    
    
        if(array == null || array.length == 0){
    
    
            return;
        }
        quick(array, 0, array.length-1);
    }
    public static void main(String[] args) {
    
    
        int[] array = {
    
    10, 9, 19, 8, 20, 8, 23, 12, 6, 24, 4, 2, 15};
        quickSort(array);
        System.out.println(Arrays.toString(array));
    }
}

归并排序

这里边界的处理有点不懂，完了记得去问一下。

public class Mergesort {
    
    
    //归并排序合并两个有序的序列。
    public void merge(int[] array,int gap){
    
    
        int left1 = 0;
        int left2 =left1+gap-1;
        int right1=left2+1;
        int right2=(right1+gap-1>array.length-1?array.length-1:right1+gap-1);
        //归并后的数组
        int[] num=new int[array.length];
        int index=0;
        //所以归并段都被排完以后，没有下一段了，left1再往后走就超出数组界限了,
        //但要考虑特殊情况，归并段只有一个元素的时候，所以这里要用right，然后特殊处理一个元素
        while (right1<=array.length-1){
    
    

            //先用lift1和右边两个比较，如果都大于右边两个那直接把右边两个放到最前面，都小于也同理。
            //如果lift1大一个小一个，那么就让lift2和right2比较，排完续往数组里放。
            while (left1<=left2&&right1<=right2){
    
    
                //2永远在1的后面，当1++到2的位置时，才能排好
                if(left1>right1){
    
    
                    num[index++]=array[right1++];
                }else {
    
    
                    num[index++]=array[left1++];
                }
            }
            //退出表示一个归并段已经完成
            //左归并段未完成
            while (left1<=left2){
    
    
                num[index++]=array[left1++];
            }
            //右归并段未完成
            while (right1<=right2){
    
    
                num[index++]=array[right1++];
            }
            //前两段排序完成，换下两段
            left1 = right2+1;
            left2 =left1+gap-1;
            right1=left2+1;
            right2=(right1+gap-1>array.length-1?array.length-1:right1+gap-1);
        }
        while (left1<array.length-1){
    
    
            num[index++]=left1++;
        }
        //这里把num[]里排好的放到array里
        for(int i=0;i<array.length-1;i++){
    
    
            array[i]=num[i];
        }

    }
}

堆排序

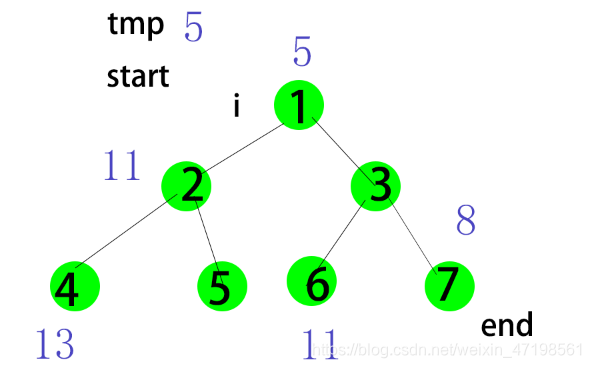
public class Heapsort {
    
    
    //用二叉树的概念
    //heapsort这个函数的作用就是找到一部分树的最大并把它放到end处。
    public static void heapsort(int[] array,int start,int end){
    
    
        //树有下标，这里创建一个起始下标，和终止下标。
        //将start下标的元素存放在变量tmp里。
        int tmp =array[start];
        //这里的循环是找儿子的过程
        for(int i =2*start+1;i<=end;i=2*i+1){
    
    
            if(i+1<=end&&array[i]<array[i+1]){
    
    
                //左儿子比右儿子小i就++到右儿子位置
                i++;
            }
            //tmo保存的都是要比较的根的值
            if(array[i]>tmp) {
    
    
                //儿子比根大就把儿子放到根处，即start处。
                array[start] = array[i];
                //继续往下找，start更新到i；
                start = i;
            }else {
    
    
                break;
            }
        }
        //最后把存在tmp的根的值放到更新到的i的位置。
        array[start]=tmp;
    }
    //从右下方最小部分树开始排序，叶子每次都对比到end处。
    public static void beginsort(int[] array){
    
    
        int change=array.length-1;
        for (int i=(array.length-1-1)/2;i>=0;i--){
    
    
            //这里end处用array.length-1不太明白
            heapsort(array,i,change);
//            change=2*i-2;
        }
        //heapsort函数将最大的值放到了最前面所以写个循环让他们从小到大
        for (int i=0;i<array.length;i++){
    
    
            int tmp =array[0];
            array[0]=array[array.length-1-i];
            array[array.length-1-i]=tmp;
            heapsort(array,0,array.length-1-i-1);
        }
    }
    public static void show(int array[]){
    
    
        for(int i=0;i<array.length;i++){
    
    
            System.out.print(array[i]);
        }
        System.out.println(" ");
    }
    public static void main(String[] args) {
    
    
        int[] arr1 =new int[]{
    
    8,5,4,9,7,2,1,5,6,4};
        int[] arr2 =new int[]{
    
    2,8,4,6,8,7,2,6};
        int[] arr3 =new int[]{
    
    5,7,9,4,5,7,5,6,3,1,7,2,8,4};
        beginsort(arr1);
        beginsort(arr2);
        beginsort(arr3);
        show(arr1);
        show(arr2);
        show(arr3);
    }
}