题目描述
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],因为3+5+3+8=19。请问该机器人能够到达多少个格子?
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof
示例 1:
输入:m = 2, n = 3, k = 1
输出:3
示例 2:
输入:m = 3, n = 1, k = 0
输出:1
解题思路
先求得每个格子的数位之和,这个可以封装成函数,走到那个格子在计算,然后判断是否小于k,可以用深度优先算法,分解成子问题,每一个格子的每一个方向都判断一下,这个题是不用回溯的,不满足条件直接返回就好了。
判断过程如下图,对第一个格子进行四个方向判断,再对这四个格子各自进行四个方向的判断…知道不满足边界条件,返回。
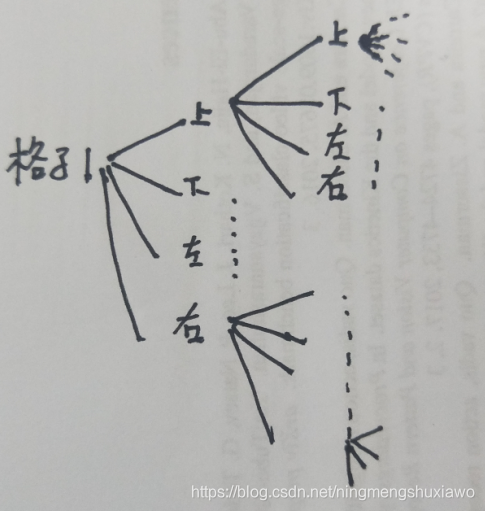
这个视频挺不错的,推荐
剑指offer机器人的运动范围-Java版
方法1:深度优先
class Solution {
int sum=0;
public int movingCount(int m,int n,int k) {
boolean[][]visited=new boolean[m][n];
return dfs(0,0,m,n,k,visited);
}
public int dfs(int x, int y, int m,int n,int k, boolean [][]visited)
{
if(x>=m||y>=n||x<0||y<0||DigitsSum(x,y)>k||visited[x][y])
return 0;
visited[x][y]=true;
sum++;//sum是全局变量,每一次搜索到符合条件的格子都会更新sum的值
//向四个方向搜索
dfs( x+1, y,m,n, k,visited);
dfs( x-1, y,m,n, k,visited);
dfs( x, y+1,m,n, k,visited);
dfs( x, y-1,m,n, k,visited);
return sum;
}
public static int DigitsSum(int x,int y)//求数位和,作为一个判断条件
{
int sum=0;
while(x!=0)
{
sum+=x%10;//求最后一位
x/=10;//去掉最后一位
}
while(y!=0)
{
sum+=y%10;
y/=10;
}
return sum;
}
}

这里的dfs还有一种写法
public int dfs(int x, int y, int k, boolean [][]visited)
{
if(x>=m||y>=n||x<0||y<0||DigitsSum(x,y)>k||visited[x][y])
return 0;
visited[x][y]=true;
sum++;
//每dfs一次都会加1,因为能dfs说明满足边界条件
return 1+dfs( x+1, y, k,visited)+dfs( x-1, y, k,visited)+dfs( x, y+1, k,visited)+dfs( x, y-1, k,visited);
//这里加1是因为如果需要进行深度搜索的话,那么第一个格子肯定是符合条件的
}

public int movingCount(int m, int n, int k) {
//临时变量visited记录格子是否被访问过
boolean[][] visited = new boolean[m][n];
return dfs(0, 0, m, n, k, visited);
}
public int dfs(int i, int j, int m, int n, int k, boolean[][] visited) {
//i >= m || j >= n是边界条件的判断,k < sum(i, j)判断当前格子坐标是否
// 满足条件,visited[i][j]判断这个格子是否被访问过
if (i >= m || j >= n || k < sum(i, j) || visited[i][j])
return 0;
//标注这个格子被访问过
visited[i][j] = true;
//沿着当前格子的右边和下边继续访问
return 1 + dfs(i + 1, j, m, n, k, visited) + dfs(i, j + 1, m, n, k, visited);
}
//计算两个坐标数字的和
private int sum(int i, int j) {
int sum = 0;
while (i != 0) {
sum += i % 10;
i /= 10;
}
while (j != 0) {
sum += j % 10;
j /= 10;
}
return sum;
}
作者:sdwwld
链接:https://leetcode-cn.com/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof/solution/dfshe-bfsliang-chong-jie-jue-fang-shi-by-sdwwld/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
减少参数的dfs
class Solution {
int m, n, k;
boolean[][] visited;
public int movingCount(int m, int n, int k) {
this.m = m; this.n = n; this.k = k;
this.visited = new boolean[m][n];
return dfs(0, 0, 0, 0);
}
public int dfs(int i, int j, int si, int sj) {
if(i >= m || j >= n || k < si + sj || visited[i][j]) return 0;
visited[i][j] = true;
return 1 + dfs(i + 1, j, (i + 1) % 10 != 0 ? si + 1 : si - 8, sj) + dfs(i, j + 1, si, (j + 1) % 10 != 0 ? sj + 1 : sj - 8);
}
}
作者:jyd
链接:https://leetcode-cn.com/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof/solution/mian-shi-ti-13-ji-qi-ren-de-yun-dong-fan-wei-dfs-b/
方法2:暴力遍历
class Solution {
int sum=1;
public int movingCount(int m,int n,int k) {
boolean[][]visited=new boolean[m][n];
return violentSolution( m, n, k, visited);
}
public int violentSolution( int m,int n,int k, boolean [][]visited){
visited[0][0]=true;
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
// if(visited[i][j]||DigitsSum(i, j)>k)
// {
// continue;
// }
if(DigitsSum(i, j)<=k)
{
// if(!visited[i][j]&&DigitsSum(i, j)<=k)
// {
// sum++;
// visited[i][j]=true;
// }
if(i+1<m&&visited[i+1][j])//i,j肯定是不会越界的(for循环决定的啊),越界只需要考虑i+1,i-1,j+1,j-1
{
sum++;
visited[i][j]=true;
}
else if(i-1>=0&&visited[i-1][j])
{
sum++;
visited[i][j]=true;
}
else if(j+1>n&&visited[i][j+1])
{
sum++;
visited[i][j]=true;
}
else if(j-1>=0&&visited[i][j-1])
{
sum++;
visited[i][j]=true;
}
}
}
}
return sum;
}
public static int DigitsSum(int x,int y)//求数位和,作为一个判断条件
{
int sum=0;
while(x!=0)
{
sum+=x%10;//求最后一位
x/=10;//去掉最后一位
}
while(y!=0)
{
sum+=y%10;
y/=10;
}
return sum;
}
}

暴力遍历的错误解法,这是我自己写的暴力解法
我的想法是每找到一个点,就判断它以及它的上下左右是否满足条件,对于某些测试案例,这是可以的,但是有些测试案例却不行,会导致结果偏大,我们分析一下,多的应该是那种它本身满足条件,但是它的上下左右都不满足条件的,那么这个点,机器人也是访问不到的
public static int violentSolution( int m,int n,int k, boolean [][]visited){
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
// if(visited[i][j]||DigitsSum(i, j)>k)
// {
// continue;
// }
if(!visited[i][j]&&DigitsSum(i, j)<=k)
{
sum++;
visited[i][j]=true;
}
if(i+1<m&&!visited[i+1][j]&&DigitsSum(i+1, j)<=k)//i,j肯定是不会越界的(for循环决定的啊),越界只需要考虑i+1,i-1,j+1,j-1
{
sum++;
visited[i+1][j]=true;
}
if(i-1>=0&&!visited[i-1][j]&&DigitsSum(i-1,j)<=k)
{
sum++;
visited[i-1][j]=true;
}
if(j+1<n&&!visited[i][j+1]&&DigitsSum(i, j+1)<=k)
{
sum++;
visited[i][j+1]=true;
}
if(j-1>=0&&!visited[i][j-1]&&DigitsSum(i, j-1)<=k)
{
sum++;
visited[i][j-1]=true;
}
}
}
return sum;
}
然后我把自己的这个方法改进了一下
但是我不知道为什么要初始化 sum=1。初始化为0的话,算出来结果小1
class Solution {
int sum=1;
public int movingCount(int m,int n,int k) {
boolean[][]visited=new boolean[m][n];
return violentSolution( m, n, k, visited);
}
public int violentSolution( int m,int n,int k, boolean [][]visited){
visited[0][0]=true;
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
if((i+1<m&&visited[i+1][j]&&DigitsSum(i+1, j)<=k)
||(i-1>=0&&visited[i-1][j]&&DigitsSum(i-1,j)<=k)
||(j+1<n&&visited[i][j+1]&&DigitsSum(i, j+1)<=k)
||(j-1>=0&&visited[i][j-1]&&DigitsSum(i, j-1)<=k))//i,j肯定是不会越界的(for循环决定的啊),越界只需要考虑i+1,i-1,j+1,j-1
//应该不需要判断<=k了,因为只有满足<=k,visited[i+1][j]才会为true
{
if(!visited[i][j]&&DigitsSum(i, j)<=k)
{
sum++;
visited[i][j]=true;
}
}
}
}
return sum;
}
public static int DigitsSum(int x,int y)//求数位和,作为一个判断条件
{
int sum=0;
while(x!=0)
{
sum+=x%10;//求最后一位
x/=10;//去掉最后一位
}
while(y!=0)
{
sum+=y%10;
y/=10;
}
return sum;
}
}
遍历的时间复杂度较高,因为深度优先遇到不满足条件的直接返回,而遍历的话,不满足条件的也会进行判断
方法3 :广度优先
https://www.bilibili.com/video/BV1E54y1d7MF?from=search&seid=2847733966988765485

class Solution {
public int movingCount(int m, int n, int k) {
if (k == 0) {
return 1;
}
Queue<int[]> queue = new LinkedList<int[]>();
// 向右和向下的方向数组
int[] dx = {
0, 1};
int[] dy = {
1, 0};
boolean[][] vis = new boolean[m][n];
queue.offer(new int[]{
0, 0});
vis[0][0] = true;
int ans = 1;
while (!queue.isEmpty()) {
int[] cell = queue.poll();
int x = cell[0], y = cell[1];
for (int i = 0; i < 2; ++i) {
int tx = dx[i] + x;
int ty = dy[i] + y;
if (tx < 0 || tx >= m || ty < 0 || ty >= n || vis[tx][ty] || get(tx) + get(ty) > k) {
continue;
}
queue.offer(new int[]{
tx, ty});
vis[tx][ty] = true;
ans++;
}
}
return ans;
}
private int get(int x) {
int res = 0;
while (x != 0) {
res += x % 10;
x /= 10;
}
return res;
}
}
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof/solution/ji-qi-ren-de-yun-dong-fan-wei-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
BFS(广度优先搜索)
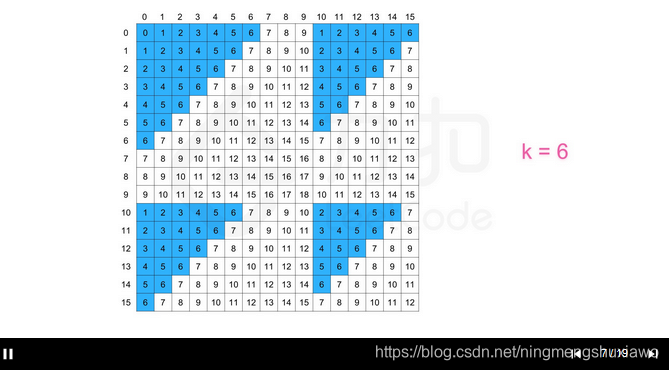
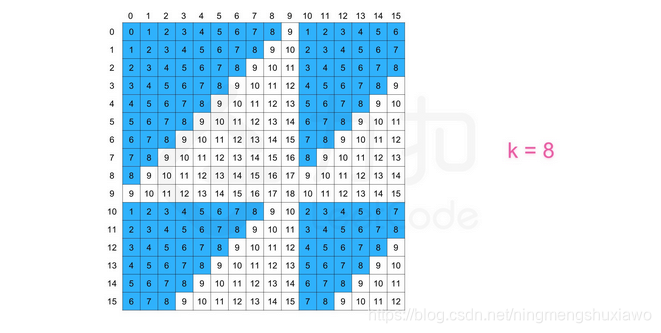
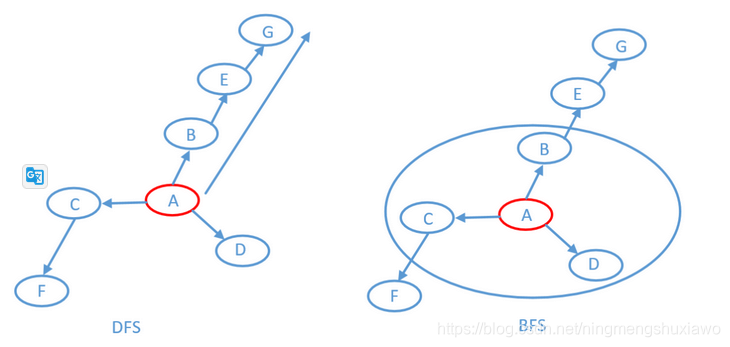
DFS是沿着一个方向一直往下走,有一种不撞南墙不回头的感觉,直到不满足条件才会回头。而BFS就显得有点博爱了,他不是一条道走下去,他会把离他最近的都访问一遍,访问完之后才开始访问第二近的……,一直这样下去,所以最好的一种数据结构就是使用队列,因为队列是先进先出,离他最近的访问完之后加入到队列中,最先入队的也是最先出队的。如下图,DFS就是沿着一条道走下去,然后再走其他的道……。BFS就是图中先访问圈内的部分,然后再把圈放大继续访问……。
作者:sdwwld
链接:https://leetcode-cn.com/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof/solution/dfshe-bfsliang-chong-jie-jue-fang-shi-by-sdwwld/
来源:力扣(LeetCode)
public int movingCount(int m, int n, int k) {
//临时变量visited记录格子是否被访问过
boolean[][] visited = new boolean[m][n];
int res = 0;
//创建一个队列,保存的是访问到的格子坐标,是个二维数组
Queue<int[]> queue = new LinkedList<>();
//从左上角坐标[0,0]点开始访问,add方法表示把坐标
// 点加入到队列的队尾
queue.add(new int[]{
0, 0});
while (queue.size() > 0) {
//这里的poll()函数表示的是移除队列头部元素,因为队列
// 是先进先出,从尾部添加,从头部移除
int[] x = queue.poll();
int i = x[0], j = x[1];
//i >= m || j >= n是边界条件的判断,k < sum(i, j)判断当前格子坐标是否
// 满足条件,visited[i][j]判断这个格子是否被访问过
if (i >= m || j >= n || k < sum(i, j) || visited[i][j])
continue;
//标注这个格子被访问过
visited[i][j] = true;
res++;
//把当前格子右边格子的坐标加入到队列中
queue.add(new int[]{
i + 1, j});
//把当前格子下边格子的坐标加入到队列中
queue.add(new int[]{
i, j + 1});
}
return res;
}
//计算两个坐标数字的和
private int sum(int i, int j) {
int sum = 0;
while (i != 0) {
sum += i % 10;
i /= 10;
}
while (j != 0) {
sum += j % 10;
j /= 10;
}
return sum;
}
方法4:递推

class Solution {
public int movingCount(int m, int n, int k) {
if (k == 0) {
return 1;
}
boolean[][] vis = new boolean[m][n];
int ans = 1;
vis[0][0] = true;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if ((i == 0 && j == 0) || get(i) + get(j) > k) {
continue;
}
// 边界判断
if (i - 1 >= 0) {
vis[i][j] |= vis[i - 1][j];
}
if (j - 1 >= 0) {
vis[i][j] |= vis[i][j - 1];
}
ans += vis[i][j] ? 1 : 0;
}
}
return ans;
}
private int get(int x) {
int res = 0;
while (x != 0) {
res += x % 10;
x /= 10;
}
return res;
}
}

