001、LeetCode134—加油站(贪心)
一开始没想太多,暴力O(n^2)
class Solution {
public int canCompleteCircuit(int[] gas, int[] cost) {
for(int i = 0; i < gas.length; i++) {
// 如果可以走一圈,直接返回即可
if(cycle(gas, cost, i)) return i;
}
// 一个都不能走一圈,返回-1
return -1;
}
// 从k走看能否走一圈
public boolean cycle(int[] gas, int[] cost, int k) {
int curIndex = k;
int leftGas = 0;
for(int i = 0; i < gas.length; i++) {
curIndex = (k + i) % gas.length;
leftGas += gas[curIndex];
if(leftGas < cost[curIndex]) return false;
leftGas -= cost[curIndex];
}
return true;
}
}
贪心做法没有想出来,比较巧妙,车能开完全程需要满足两个条件:
- 车从
i站能开到i+1。 - 所有站里的油总量要
>=车子的总耗油量。
假设从编号为0站开始,一直到k站都正常,在开往k+1站时车子没油了。这时,应该将起点设置为k+1站
class Solution {
public int canCompleteCircuit(int[] gas, int[] cost) {
int rest = 0, run = 0, start = 0;
// run = gas[i] - cost[i] 的总和
// 如果run的值小于0了就要重置,代表这个区间不行
// 如果总和小于0,直接返回-1即可
for(int i = 0; i < gas.length; i++) {
run += gas[i] - cost[i];
rest += gas[i] - cost[i];
if(run < 0) {
start = i + 1;
run = 0;
}
}
return rest < 0 ? -1:start;
}
}
002、LeetCode1696—跳跃游戏IV(动态规划 + 单调队列)
220场周赛的第三题,当时写出来了,但是因为用例太少,是个错误的答案给过了
正确做法应该是用dp搭配单调队列
dp的用法在于:dp[i]代表以i结尾的答案,dp[i] = max(dp[i-k]、dp[i-k+1] ... dp[i-1]),再加上nums[i]即可
而用单调队列是用来简化这个找前k个元素最大值的作用
class Solution {
public int maxResult(int[] nums, int k) {
int[] dp = new int[nums.length];
int len = nums.length;
dp[0] = nums[0];
for(int i = 1; i < len; i++){
int maxval = dp[i - 1];
for(int j = i - 2; j >= i - k && j >= 0; j--){
if(dp[j] > maxval){
maxval = dp[j];
}
if(nums[j] > 0){
break;
}
}
dp[i] = maxval + nums[i];
}
return dp[len - 1];
}
}
003、LeetCode455—分发饼干(贪心)
贪心入门题目,简单来说就是让吃的少的尽量吃小饼干
因为涉及到排序,故时间复杂度为排序的时间复杂度O(logn),空间复杂度O(1)
class Solution {
public int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
int ans = 0;
int cookieIndex = 0;
for(int child : g) {
while(cookieIndex < s.length && s[cookieIndex] < child) {
cookieIndex++;
}
if(cookieIndex >= s.length) return ans;
ans++;
cookieIndex++;
}
return ans;
}
}
004、LeetCode23—合并K个升序链表(分治、堆)
是一道LeetCode困难题目,本质上我们首先要知道如何合并两个有序的数组(链表),无非是两个指针不断移动。如何合并K个链表呢?
首先想到的是:不断两个两个合并,长度为n的链表数组需要n - 1 次合并,实现如下:
暴力法
/**
* - 时间复杂度:O(2*m*n)因为合并了数组长度n-1次,每次合并都要遍历两个链表m长度
* - 空间复杂度:O(m)递归栈的深度
*/
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
if(lists.length == 0) return null;
if(lists.length == 1) return lists[0];
for(int i = 1; i < lists.length; i++) {
// 不断和前面一个链表合并
// 将合并后的链表保存到原数组中
lists[i] = mergeTwo(lists[i], lists[i-1]);
}
return lists[lists.length - 1];
}
// 合并两个链表
public ListNode mergeTwo(ListNode a, ListNode b) {
if(a == null) return b;
if(b == null) return a;
if(a.val > b.val) {
b.next = mergeTwo(a, b.next);
return b;
} else {
a.next = mergeTwo(a.next, b);
return a;
}
}
}
但是这样的效率太低了,我们不需要按顺序每次合并两个,而是两个两个合并,最后剩下一个即可,所以我们可以用分治的思想不断合并:
分治法
/**
* 时间复杂度:O(nm * logn)
* mn指的是链表数组中每个节点都要被遍历一次
* logn指的是最后合并排序数组时需要logn次
* 空间复杂度:O(logn)
* 指的是merge递归栈的空间
*/
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
return merge(lists, 0, lists.length-1);
}
// 分治
public ListNode merge(ListNode[] lists, int l, int r){
if(l > r) return null;
if(l == r) return lists[l];
if(l + 1 == r) return mergeTwo(lists[l], lists[r]);
int mid = (l + r) >> 1;
return mergeTwo(merge(lists, l, mid), merge(lists, mid+1, r));
}
// 合并两个有序链表成为一个有序链表
public ListNode mergeTwoLists(ListNode a, ListNode b) {
if(a == null) return b;
if(b == null) return a;
if(a.val > b.val) {
b.next = mergeTwoLists(a, b.next);
return b;
} else {
a.next = mergeTwoLists(a.next, b);
return a;
}
}
}
除了以上方法,我们可以想到如果用优先队列来处理,只需要用一个最小堆来保存所有链表,然后每次弹出最小值的时候,如果该链表还有next,则将next入堆中,即可保持最小堆并且不漏元素
/**
* 时间复杂度:O(mn * logmn) 每个点都被插入删除各一次
* 空间复杂度:O(mn) 堆的大小,即节点数量
*/
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
// 最小堆
Queue<ListNode> queue =
new PriorityQueue<>((a, b) -> (a.val - b.val));
// 将所有链表头节点加入堆中
for(ListNode list : lists){
if(list != null) queue.add(list);
}
// 构建返回链表
ListNode ans = new ListNode(-1);
ListNode cur = ans;
while(!queue.isEmpty()){
ListNode min = queue.poll();
cur.next = min;
// 如果弹出来节点还有next,就将next加入堆中
if(min.next != null) {
queue.add(min.next);
}
cur = cur.next;
}
return ans.next;
}
}
005、LeetCode451——根据字符出现频排序(hash、堆)
题目比较简单,但是比较全面,就是构建一个hash表,如何根据其value进行排队,然后组装成新的字符串,Java中没有现成的方法可以做到,所以涉及到一些额外的存储空间,这里主要有两种方法可以实现
第一种是将Entry节点放到List集合中,然后自定义排序规则,用工具类Collections排序
/**
* n为字符串s的长度
* 时间复杂度:O(nlogn)排序的复杂度
* 空间复杂度:O(n)hash表和列表所占空间
*/
class Solution {
public String frequencySort(String s) {
StringBuilder sb = new StringBuilder();
Map<Character, Integer> map = new HashMap<>();
for(int i = 0; i < s.length(); i++) {
map.put(s.charAt(i), map.getOrDefault(s.charAt(i), 0) + 1);
}
List<Map.Entry<Character, Integer>> list =
new ArrayList<Map.Entry<Character, Integer>>(map.entrySet());
Collections.sort(list, (a, b) -> (b.getValue() - a.getValue()));
for(Map.Entry e:list) {
for(int i = 0; i < (int)e.getValue(); i++) {
sb.append(e.getKey());
}
}
return sb.toString();
}
}
第二种方法是将节点构建成一个堆,然后不断出堆即可
/**
* n为字符串s的长度
* 时间复杂度:O(nlogn)每个节点入堆出堆
* 空间复杂度:O(n)
*/
class Solution {
public String frequencySort(String s) {
StringBuilder sb = new StringBuilder();
Map<Character, Integer> map = new HashMap<>();
for(int i = 0; i < s.length(); i++) {
map.put(s.charAt(i), map.getOrDefault(s.charAt(i), 0) + 1);
}
PriorityQueue<Map.Entry<Character, Integer>> queue =
new PriorityQueue<>((a, b) -> (b.getValue() - a.getValue()));
queue.addAll(map.entrySet());
while(!queue.isEmpty()) {
for(int i = 0; i < queue.peek().getValue(); i++){
sb.append(queue.peek().getKey());
}
queue.poll();
}
return sb.toString();
}
}
006、LeetCode5210—球会落何处(dfs)
周赛第三题,因为再死磕第二题没有做,实际上不是很难
思路我是按照题目的意思模拟不断遍历实现的,代码可读性较差。
实际上这种题目应该适用递归dfs,还是做的少,这里mark一下,
我的思路这里不放了。直接看dfs吧
class Solution:
def findBall(self, grid: List[List[int]]) -> List[int]:
m,n = len(grid), len(grid[0])
def dfs(i, j):
if j < 0 or j >= n: return -1
if i >= m: return j
if j + 1 < n and grid[i][j] == 1 and grid[i][j+1] == -1:
return -1
if j - 1 > -1 and grid[i][j] == -1 and grid[i][j-1] == 1:
return -1
if grid[i][j] == 1:
return dfs(i+1, j+1)
return dfs(i+1,j-1)
return [dfs(0, j) for j in range(n)]
007、LeetCode378—有序矩阵中的第k小的元素(二分、堆)
本题目题意比较明确,我们都知道排序数组查找元素要用二分法,但是本题目是一个二维矩阵,如何能用二分法查找要找的元素呢?答案是沿着对角线(最大值和最小值)往中间查找,mid = (left + right) / 2,之后根据题意查找< mid的数量,和k做比较,更新left或者right直到找到
/**
* 时间复杂度:O(n log(max - min))
* 二分查找次数:long(max - min)
* 每次消耗的时间复杂度:n
* 空间复杂度:O(1)
*/
class Solution {
public int kthSmallest(int[][] matrix, int k) {
int row = matrix.length;
int col = matrix[0].length;
int min = matrix[0][0];
int max = matrix[row - 1][col - 1];
while (min < max) {
// 每次循环都保证第K小的数在start~end之间,当start==end,第k小的数就是start
int mid = (min + max) / 2;
// 找二维矩阵中<=mid的元素总个数
int count = findNotBiggerThanMid(matrix, mid, row, col);
if (count < k) {
// 第k小的数在右半部分,且不包含mid
min = mid + 1;
} else {
// 第k小的数在左半部分,可能包含mid
max = mid;
}
}
return max;
}
// 找二维矩阵中<=mid的元素总个数
private int findNotBiggerThanMid(int[][] matrix, int mid, int row, int col) {
// 以列为单位找,找到每一列最后一个<=mid的数即知道每一列有多少个数<=mid
int i = row - 1;
int j = 0;
int count = 0;
while (i >= 0 && j < col) {
if (matrix[i][j] <= mid) {
// 第j列有i+1个元素<=mid
count += i + 1;
j++;
} else {
// 第j列目前的数大于mid,需要继续在当前列往上找
i--;
}
}
return count;
}
}
如上这种思路不是很容易想到,假使我们不利用列递增的顺序,可以使用一种容易理解的解法:
即每个数组首位放在堆中,然后不断出堆k次,每次出完堆后将该数组第二个元素放到堆中,如此反复,最后得出的元素即为答案
/**
* 时间复杂度:O(n *n * logn)可能有n*n次操作
* 空间复杂度:O(n)n个node结点
*/
class Solution {
class Node{
int index = 0;
int[] array;
Node(int[] array, int index){
this.array = array;
this.index = index;
}
}
public int kthSmallest(int[][] matrix, int k) {
Queue<Node> queue =
new PriorityQueue<>((a, b) -> (a.array[a.index] - b.array[b.index]));
for(int[] array : matrix) {
queue.add(new Node(array, 0));
}
int ans = 0;
Node cur = null;
while(k-- != 0){
cur = queue.poll();
ans = cur.array[cur.index];
if(cur.array.length - 1 != cur.index) {
queue.add(new Node(cur.array, cur.index + 1));
}
}
return ans;
}
}
008、LeetCode1054—距离相等的条形码(hash、堆)
建立hash表,对应数字和出现的次数。然后根据次数放入大顶堆中,每次取出堆中前2大的元素放入ans数组中,如果value值大于1,就将value减一再放入堆中,最后针对奇数个数收尾即可
/**
* - 时间复杂度:O(nlogn)n为数组中不相同的元素的个数
* - 空间复杂度:O(n)
*/
class Solution {
public int[] rearrangeBarcodes(int[] barcodes) {
int[] ans = new int[barcodes.length];
int ansIndex = 0;
Map<Integer, Integer> map = new HashMap<>();
for(int num : barcodes) {
map.put(num, map.getOrDefault(num, 0) + 1);
}
Queue<Map.Entry<Integer, Integer>> queue = new PriorityQueue<>((a,b) -> (b.getValue() - a.getValue()));
queue.addAll(map.entrySet());
// 当堆中有两个及以上的节点时,poll出两个保存
while(queue.size() > 1){
Map.Entry<Integer, Integer> e1 = queue.poll();
Map.Entry<Integer, Integer> e2 = queue.poll();
ans[ansIndex++] = e1.getKey();
ans[ansIndex++] = e2.getKey();
// 如果节点数量还有就再加进去
if(e1.getValue() > 1){
e1.setValue(e1.getValue() - 1);
queue.add(e1);
}
if(e2.getValue() > 1){
e2.setValue(e2.getValue() - 1);
queue.add(e2);
}
}
// 针对奇数个进行收尾
if (!queue.isEmpty()) {
ans[ansIndex++] = queue.poll().getKey();
}
return ans;
}
}
009、LeetCode120-三角形最小路径和(动态规划)
解决动态规划问题的第一步就是找到状态转移方程。
本题目中,如过求从三角形顶点到底部的最小路径和,如果我们用func来表示整个函数,则我们可以得出min = triangle[0][0] + fun(tarngle[1][0], trangle[1][1])
递归解决方法:
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
return dfs(triangle, 0, 0);
}
public int dfs(List<List<Integer>> triangle, int i, int j){
if(i == triangle.size()){
return 0;
}
return Math.min(dfs(trangle, i+1, j), dfs(trangle. i+1, j+1)) + trangle.get(i).get(j);
}
}
但是这样做的时间复杂度和空间复杂度太高,我们想优化以下,于是用自定向下的递归变为自定向上的递推dp
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int n = triangle.size();
// dp[i][j] 表示从点 (i, j) 到底边的最小路径和。
int[][] dp = new int[n + 1][n + 1];
// 从三角形的最后一行开始递推。
for (int i = n - 1; i >= 0; i--) {
for (int j = 0; j <= i; j++) {
dp[i][j] = Math.min(dp[i + 1][j], dp[i + 1][j + 1]) + triangle.get(i).get(j);
}
}
return dp[0][0];
}
}
在上述代码中,我们定义了一个 NN 行 NN 列 的 dpdp 数组(NN 是三角形的行数)。
但是在实际递推中我们发现,计算 dp[i][j] 时,只用到了下一行的 dp[i + 1][j]和dp[i + 1][j + 1]。因此 dp数组不需要定义 N 行,只要定义1行就行。所以我们稍微修改一下上述代码,将 i 所在的维度去掉(如下),就可以将 O(N^2)的空间复杂度优化成O(N)
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int n = triangle.size();
int[] dp = new int[n + 1];
for (int i = n - 1; i >= 0; i--) {
for (int j = 0; j <= i; j++) {
dp[j] = Math.min(dp[j], dp[j + 1]) + triangle.get(i).get(j);
}
}
return dp[0];
}
}
010、LeetCode64-最小路径和(动态规划)
本题目和上一道题目很类似,状态转移方程为dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
但是处理边界值的时候需要注意,如果不能修改原数组
/**
* 时间复杂度: O(m)(n)
* 空间复杂度:O(m)(n)
*/
class Solution {
public int minPathSum(int[][] grid) {
int[][] dp = new int[grid.length + 1][grid[0].length + 1];
for(int[] array : dp){
Arrays.fill(array, Integer.MAX_VALUE);
}
for(int i = 0; i < grid.length; i++){
for(int j = 0; j < grid[0].length; j++) {
if(i == 0 && j == 0){
dp[i+1][j+1] = grid[i][j];
continue;
}
dp[i+1][j+1] = grid[i][j] + Math.min(dp[i][j+1], dp[i+1][j]);
}
}
return dp[dp.length -1][dp[0].length - 1];
}
}
如果可以修改原来的数组,则
/**
* 时间复杂度: O(m)(n)
* 空间复杂度:O(1)
*/
class Solution {
public int minPathSum(int[][] grid) {
int width = grid[0].length, high = grid.length;
if (high == 0 || width == 0) return 0;
// 初始化
for (int i = 1; i < high; i++) {
grid[i][0] += grid[i - 1][0];
}
for (int i = 1; i < width; i++) {
grid[0][i] += grid[0][i - 1];
}
for (int i = 1; i < high; i++)
for (int j = 1; j < width; j++)
grid[i][j] += Math.min(grid[i - 1][j], grid[i][j - 1]);
return grid[high - 1][width - 1];
}
}
011、LeetCode239-滑动窗口的最大值(单调队列、滑动窗口)
本题目是一个比较典型的双端单调队列题目。题目意思也比较容易理解。
- 我们先构造一个单调队列,里面保存的不是数组中的值,而是索引。
- 设定滑动窗口的右边界,不断遍历
- 如果此时的右边界的索引减去单调队列队头超过了滑动窗口大小,队头就出队
- 当出现队列里面的值小于此时右边界值时,就出栈,直到满足条件或者全部出栈
- 将右边界索引入队
- 当右边界达到滑动窗口大小,保存队列头元素到ans数组
/**
* 时间复杂度:O(n) 遍历一次
* 空间复杂度:O(n) 双端单调队列
*/
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
// 单调队列,里面存的是数组索引
Deque<Integer> queue = new LinkedList<>();
int[] ans = new int[nums.length - k + 1];
int right = 0;
for(; right < nums.length; right++) {
if(!queue.isEmpty() && right - queue.getFirst() == k){
queue.removeFirst();
}
while(!queue.isEmpty() && nums[queue.getLast()] < nums[right]) {
queue.removeLast();
}
queue.addLast(right);
if(right >= k - 1) ans[right - k + 1] = nums[queue.getFirst()];
}
return ans;
}
}
012、LeetCode162-寻找峰值(二分)
本题目的二分的使用比较巧妙。
首先nums[mid] > nums[mid+1]说明了什么?答案是说明了左侧一定有一个极值,因为即使在中间没有升序的,最左侧大于也一定满足,同理nums[mid] < nums[mid+1]也是一个意思,右边一定有一个极值,即使右边中间没有,最右边值也是满足的(可以用两个单调数组来试一下)
由此我们就可以使用二分法将时间复杂度降低到O(logn)
/**
* 时间复杂度:O(logn)
* 空间复杂度:O(1)
*/
public class Solution {
public int findPeakElement(int[] nums) {
int l = 0, r = nums.length - 1;
while (l < r) {
int mid = (l + r) / 2;
if (nums[mid] > nums[mid + 1])
r = mid;
else
l = mid + 1;
}
return l;
}
}
013、LeetCode1712-将数组分成三个子数组的方案数(前缀和、高级二分)
周赛题目,使用的是两层for循环的O(n^2),超时了,可以优化为O(nlogn)
后来才想到,对于一个全是正数的数组前缀和,本来就是单调递增的的,可以使用二分法找到左右边界。
但是本题目的二分比较难,边界条件需要注意地方很多
/**
* 时间复杂度:O(nlogn): for + 二分
* 空间复杂度:O(n): 前缀和数组,当然如果可以修改原数组直接变为前缀和就可
*/
class Solution {
public int waysToSplit(int[] nums) {
int[] preSum = new int[nums.length];
int sum = 0;
for(int i = 0; i < nums.length; i++){
sum += nums[i];
preSum[i] = sum;
}
int ans = 0;
int left = 0, right = 0; // 二分使用,左右边界
for(int i = 0; i < preSum.length; i++) {
if(preSum[i] > preSum[preSum.length-1] / 3) break;
left = findLeft(i, i+1, preSum.length-1, preSum);
right = findRight(i, i+1, preSum.length-1, preSum);
ans += right - left;
ans = ans % 1000000007; // 每次对结果取下余
}
return ans % 1000000007;
}
// 二分法找左边界
public int findLeft(int i, int left, int right, int[] preSum){
while(right > left) {
int mid = left + ((right - left) >> 1);
int leftSum = preSum[i];
int midSum = preSum[mid] - leftSum;
int rightSum = preSum[preSum.length-1] - preSum[mid];
if(midSum >= leftSum && rightSum >= midSum){
right = mid;
} else if (rightSum < midSum){
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
// 二分法找右边界
public int findRight(int i, int left, int right, int[] preSum){
while(right > left) {
int mid = left + ((right - left) >> 1);
int leftSum = preSum[i];
int midSum = preSum[mid] - leftSum;
int rightSum = preSum[preSum.length-1] - preSum[mid];
if(midSum >= leftSum && rightSum >= midSum){
left = mid + 1;
} else if (rightSum < midSum){
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
}
014、LeetCode004-寻找两个正序数组的中位数(高级二分)
本题目之所以是困难题目是因为要求时间复杂度为O(log(m+n)),如果是O(m+n)我们利用双指针法很简单就可以得出
之所以叫这个题目为高级二分是因为,它的二分使用并不是基于“两个数组是排序的”这一个规则直接衍生的二分。而是利用一种巧妙地折半删除的方法一步一步删除不符合题意的答案(小于中位数的答案),最后得出正确答案。
另外有一点可以通用的小技巧是,在涉及到奇数和偶数两个情况下不同的边界判断情况时,不妨采取这里的思路:
// 数组 nums 的 中位数 ,count为nums数组总长度,中位数为:
double mid = nums[(count - 1) / 2] + nums[count / 2]) / 2.0;
代码:
class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int len1 = nums1.length;
int len2 = nums2.length;
int total = len1 + len2;
int left = (total + 1) / 2;
int right = (total + 2) / 2;
return (findK(nums1, 0, nums2, 0, left) + findK(nums1, 0, nums2, 0, right)) / 2.0;
}
// 找到两个数组中第k小的元素
// i: nums1的起始位置 j: nums2的起始位置
public int findK(int[] nums1, int i, int[] nums2, int j, int k) {
if (i >= nums1.length)
return nums2[j + k - 1];
if (j >= nums2.length)
return nums1[i + k - 1];
if (k == 1) {
return Math.min(nums1[i], nums2[j]);
}
// 计算出每次要比较的两个数的值,来决定 "删除"" 哪边的元素
int mid1 = (i + k / 2 - 1) < nums1.length ? nums1[i + k / 2 - 1] : Integer.MAX_VALUE;
int mid2 = (j + k / 2 - 1) < nums2.length ? nums2[j + k / 2 - 1] : Integer.MAX_VALUE;
//通过递归的方式,来模拟删除掉前K/2个元素
if (mid1 < mid2) {
return findK(nums1, i + k / 2, nums2, j, k - k / 2);
}
return findK(nums1, i, nums2, j + k / 2, k - k / 2);
}
}
015、LeetCode399-除法求值(并查集)
题目巧妙地将并查集和带权图结合起来,比较难
在并查集里面用weight数组代表指向的父结点的权值,并在union的时候及时更新weight数组,这样便可以知道任意两个数的比值
public class Solution {
public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries){
int equationsSize = equations.size();
UnionFind unionFind = new UnionFind(2 * equationsSize);
// 第 1 步:预处理,将变量的值与 id 进行映射,使得并查集的底层使用数组实现,方便编码
Map<String, Integer> hashMap = new HashMap<>(2 * equationsSize);
String A = null, B = null;
for (int i = 0; i < equationsSize; i++) {
List<String> equation = equations.get(i);
A = equation.get(0);
B = equation.get(1);
if (!hashMap.containsKey(A)) {
hashMap.put(A, i*2);
}
if (!hashMap.containsKey(B)) {
hashMap.put(B, i*2+1);
}
unionFind.union(hashMap.get(A), hashMap.get(B), values[i]);
}
// 第 2 步:做查询
int queriesSize = queries.size();
double[] res = new double[queriesSize];
for (int i = 0; i < queriesSize; i++) {
A = queries.get(i).get(0);
B = queries.get(i).get(1);
if (!hashMap.containsKey(A) || !hashMap.containsKey(B)) {
res[i] = -1.0d;
} else {
res[i] = unionFind.isConnected(hashMap.get(A), hashMap.get(B));
}
}
return res;
}
// 带权值的并查集
private class UnionFind {
private int[] parent;
// 指向的父结点的权值
private double[] weight;
public UnionFind(int n) {
this.parent = new int[n];
this.weight = new double[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
weight[i] = 1.0d;
}
}
public void union(int x, int y, double value) {
int rootX = find(x);
int rootY = find(y);
if (rootX == rootY) return;
parent[rootX] = rootY;
// 更新weight,具体查看题解
weight[rootX] = weight[y] * value / weight[x];
}
/**
* 路径压缩
* @return 根结点的 id
*/
public int find(int x) {
if (x != parent[x]) {
int origin = parent[x];
parent[x] = find(parent[x]);
weight[x] *= weight[origin];
}
return parent[x];
}
public double isConnected(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX == rootY) {
return weight[x] / weight[y];
} else {
return -1.0d;
}
}
}
}
016、LeetCode438-找到字符串中所有字母异位词(双指针,滑动窗口,hash)
根据题意我们直到本题目应该使用滑动窗口,并且要构建双指针。值得注意的是因为都是小写字母,我们可以用int[26]来替代哈希表
然后不断更新left 和 right指针即可。
这里需要注意的是,不需要每次循环过来就删除最左边元素,而是在添加right元素的时候如果不成立循环删除最左元素即可,最后只要滑动窗口大导要求的长度直接可以放入结果集
/**
* 时间复杂度:O(n) n为s的长度
* 空间复杂度:O(1) 两个int[26]的数组
*/
class Solution {
public List<Integer> findAnagrams(String s, String p) {
List<Integer> ans = new ArrayList<>();
// 构建needs数组
int[] needs = new int[26];
for(int i = 0; i < p.length(); i++){
needs[p.charAt(i) - 'a']++;
}
int[] cmp = new int[26];
int left = 0, right = 0;
while(right < s.length()) {
int curR = s.charAt(right) - 'a';
cmp[curR]++;
while (cmp[curR] > needs[curR]) {
int curL = s.charAt(left) - 'a';
cmp[curL] -= 1;
left++;
}
right++;
if(right - left == p.length()){
ans.add(left);
}
}
return ans;
}
}
017、LeetCode228-汇总区间(双指针)
本题目是一道简单题,并且思路也比较简单,但是细节很多需要注意
碰到这样的题目很明显就应该使用双指针来解决,从而避免了边界值的讨论。
也就是说,在刷题的时候,有意识地将题目归类到自己做过的类型,使用适应的数据结构和方法来解题,避免自己思考题目,按照自己的想法来组织代码
class Solution {
public List<String> summaryRanges(int[] nums) {
List<String> ans = new ArrayList<>();
int i = 0;
for(int j = 0; j < nums.length; j++) {
// 如果不满足 nums[j+1] = nums[j] + 1
// 或者到最后一个元素的时候
if(j == nums.length - 1 || nums[j] + 1 != nums[j+1]) {
StringBuilder sb = new StringBuilder();
if(i != j) {
sb.append(nums[i]).append("->");
}
sb.append(nums[j]);
ans.add(sb.toString());
i = j + 1;
}
}
return ans;
}
}
018、LeetCode0101-判断字符是否唯一(位运算)
使用的前提是保证该字符串都是小写字符。一个int类型相当于一个boolean[32]的数组,来表示一个字符是否出现过。用字符的大小标示移位即可。
需要注意的是&、|、^这些性质和用法
class Solution {
public boolean isUnique(String astr) {
int mark = 0;
for(char ch : astr.toCharArray()) {
int index = ch - 'a';
// 如果已经出现过了
if((mark & (1 << index)) != 0) {
return false;
} else {
mark |= (1 << index);
}
}
return true;
}
}
019、LeetCode401-二进制手表(位运算)
回溯没有写出来,本题目如果用位运算来解思路比较清晰:
- 首先明白因为时针最多有4个亮,又因为要满足[0,11],所以最多应该是3个,同理证明分针范围是[0,5]。所以本题目
num最多就是8。 - 也就是说答案有限的,我们只要将这些情况一一罗列下来,看看是否满足题解的条件即可。
- 用一个长度为10的二进制数,前四位代表时针(1代表亮,0代表灭)。后6为代表分针,遍历所有情况(时针[0, 11], 分针[0, 59])
- 如果满足
前四位亮的数量 + 后六位亮的数量 = num,就放进答案
这里的技巧是,遍历[0, 11],然后将这个数向左移动6位 和 分针[0, 59]做与运算,在调用java中的Integer.bitCount()就知道一共有几个1了
class Solution {
public List<String> readBinaryWatch(int num) {
List<String> ans = new ArrayList<>();
for(int i = 0; i < 12; i++) {
for(int j = 0; j < 60; j++) {
if(Integer.bitCount((i << 6) | j) == num) {
ans.add(i + (j >= 10? ":" : ":0") + j);
}
}
}
return ans;
}
}
020、LeetCode684-冗余连接(并查集)
本题目是并查集比较经典一道题目,用到了并查集的一个很重要的作用—判断图中是否有环
在执行并查集的union操作时,其中如果两个节点在一个子域中,我们一半不操作,这个时候就是该图中出现环的时候。又因为题中说明**该图由一个N个节点的树以及一条附加的边构成… 返回一条可以删去的边,使得结果图是一个有着N个节点的树 **。所以多余的边一定在最后。我们只要执行unoin操作,然后当出现环的是否返回即可
class Solution {
public int[] findRedundantConnection(int[][] edges) {
int N = edges.length;
int[] ans = new int[2];
DSU dsu = new DSU(N + 1);
for(int[] edge : edges) {
if(!dsu.union(edge[0], edge[1])){
ans[0] = edge[0];
ans[1] = edge[1];
return ans;
}
}
return ans;
}
// 并查集模板
private class DSU{
int[] p, rank;
DSU(int N) {
p = new int[N];
for(int i = 0; i < N; i++)
p[i] = i;
rank = new int[N];
}
public int find(int x){
if(x != p[x]){
p[x] = find(p[x]);
}
return p[x];
}
public boolean union(int x, int y){
int xR = find(x);
int yR = find(y);
if(xR == yR) return false;
if(rank[xR] > rank[yR]) {
p[xR] = yR;
} else if(rank[xR] < rank[yR]){
p[yR] = xR;
} else {
p[yR] = xR;
rank[xR]++;
}
return true;
}
}
}
021、LeetCode51-N皇后(回溯)
本题目是一道经典的回溯题目,这里需要明白的是,回溯算法本质上是一种暴力穷举的算法,性能并不算高,之所以有这种算法是因为有些题目能用暴力算法就已经可以了。
N皇后的规则需要提前知道:任意两个皇后之间不能再同一行、同一列、同一个对角线上
然后我们的思路就是从这个N * N的第一行确定一个点,然后往下走,如果走到最后一行就算一次成功,中间每次走一步都要判断是否满足N皇后的性质,需要我们另写代码判断。回溯思想的利用就在于,如果这一步走错了可以返回上一步,然后就是细节方面的处理
/**
* - 时间复杂度:O(n!) 第一行确定后,第二行有n - 1 个选择
* - 空间复杂度:O(1) 递归栈深度最大为9
*/
class Solution {
public List<List<String>> solveNQueens(int n) {
char[][] chess = new char[n][n];
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
chess[i][j] = '.';
List<List<String>> res = new ArrayList<>();
solve(res, chess, 0);
return res;
}
private void solve(List<List<String>> res, char[][] chess, int row) {
if (row == chess.length) {
res.add(construct(chess));
return;
}
for (int col = 0; col < chess.length; col++) {
if (valid(chess, row, col)) {
chess[row][col] = 'Q';
solve(res, chess, row + 1);
chess[row][col] = '.';
}
}
}
//row表示第几行,col表示第几列
private boolean valid(char[][] chess, int row, int col) {
//判断当前列有没有皇后,因为他是一行一行往下走的,
//我们只需要检查走过的行数即可,通俗一点就是判断当前坐标位置的上面有没有皇后
for (int i = 0; i < row; i++) {
if (chess[i][col] == 'Q') {
return false;
}
}
//判断当前坐标的右上角有没有皇后
for (int i = row - 1, j = col + 1; i >= 0 && j < chess.length; i--, j++) {
if (chess[i][j] == 'Q') {
return false;
}
}
//判断当前坐标的左上角有没有皇后
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (chess[i][j] == 'Q') {
return false;
}
}
return true;
}
//把数组转为list
private List<String> construct(char[][] chess) {
List<String> path = new ArrayList<>();
for (int i = 0; i < chess.length; i++) {
path.add(new String(chess[i]));
}
return path;
}
}
022、LeetCode695-岛屿的最大面积(DFS)
本题目是一道比较有代表性的搜索dfs题目,不难想到可以遍历图中每个点,然后看看从该点扩散可以找到多大的面积,最后选出最大的点即可。
但是这样做的时间复杂度较高,我们应该进行合理的剪枝操作 。即对于走过的陆地来说,我们其实没有必要再走一遍,因为它所代表的那一块儿陆地已经被前面的点计算过了。所以我们这里对于每个走过的陆地,直接将它变为海洋。最后递归前后左右加起来取最值即可
/**
* 时间复杂度:O(m*n) 每个点都要且只访问一次
* 空间复杂度:O(m*n) 对于全是空地的点,递归栈的深度最坏是全部点
*/
class Solution {
public int maxAreaOfIsland(int[][] grid) {
int max = 0;
for(int i = 0; i < grid.length; i++) {
for(int j = 0; j < grid[i].length; j++) {
max = Math.max(max, dfs(grid, i, j));
}
}
return max;
}
public int dfs(int[][] grid, int i, int j) {
if(grid[i][j] == 0) return 0;
// 每访问一个空地,将它标为已经访问过,以后不再访问
grid[i][j] = 0;
// 前后左右四个方向走一遍
int up = 0, down = 0, left = 0, right = 0;
if(i > 0) up = dfs(grid, i-1, j);
if(i + 1 < grid.length) down = dfs(grid, i+1, j);
if(j > 0) left = dfs(grid, i, j-1);
if(j + 1 < grid[i].length) right = dfs(grid, i, j+1);
return up + down + left + right + 1;
}
}
023、ACwing680-剪绳子 (浮点数二分)
今日头条2019年的笔试题,如果直接想实际上很难想,必须归类到已有的数据结构和算法
不难知道,对于这么多根子,如果知道一个长度x,让我们计算这堆绳子产生几条x长度的绳子我们是有办法计算的,即对于每一根都可以整除,最后将结果汇总就是答案
但是我们不知道这个x是多少,答案也让我们求x。我们可以知道的是x的范围:(0, 10e9]。于是我们可以使用二分的思想来不断将结果减半,最后试验出最大的绳子长度。
因为是浮点数保留2位小数,我们在使用二分范围时认为在10e4内就算通过。(+2)
import java.util.*;
/**
* 时间复杂度:O(nlogn) n是执行一次check()的时间复杂度, logn是执行二分的复杂度
* 空间复杂度:O(1)
*/
public class Main{
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(), m = sc.nextInt();
int[] rings = new int[n];
for(int i = 0; i < n; i++) {
rings[i] = sc.nextInt();
}
double l = 0, r = 1e9;
while(r - l > 1e-4) {
double mid = (l + r) / 2.0;
// 如果剪出来满足条件,就继续向最大值找
if(check(rings, mid) >= m){
l = mid;
} else {
r = mid;
}
}
System.out.println(String.format("%.2f", l));
}
// 计算当前长度下,一共可以剪出几条这样长度的绳子
public static int check(int[] rings, double mid) {
int num = 0;
for(int i = 0; i < rings.length; i++) {
num += rings[i] / mid;
}
return num;
}
}
024、ACwing1227-分巧克力(整数二分)
本题目和上一道题目搭配食用
整体思路和上一道差不多。即在知道答案的范围,我们使用二分法不断逼近。最后用对数级别的复杂度去寻找答案。
整数二分相比于浮点数二分法需要考虑边界问题,即mid向哪边取整的问题,唯一的法则是,根据题目灵活处理。
import java.util.*;
public class Main{
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(), k = sc.nextInt();
int[] h = new int[n], w = new int[n];
for(int i = 0; i < n; i++){
h[i] = sc.nextInt();
w[i] = sc.nextInt();
}
int l = 1, r = 100000;
while(l < r) {
int mid = l + r >> 1;
if(check(mid, h, w, k)){
l = mid + 1;
} else {
r = mid;
}
}
System.out.println(l - 1);
}
public static boolean check(int mid, int[] h, int[] w, int k) {
long res = 0;
for(int i = 0; i < h.length; i++) {
// 长和边分别整除再相乘可以算出本面积可以产出多少个mid边长的正方形
res += (w[i] / mid) * (h[i] / mid);
}
return res >= k;
}
}
025、LeetCode1162-地图分析(BFS)
本题目是一道比较有代表性的BFS题目。
- 对所有的land,同时进行扩散,最后扩散到的地方一定是最大值,扩散的次数就是这个曼哈顿距离。
- 为了不重复走,这里对扩散到的每一层都执行上一层的值+1操作,因为land最开始是1,所以最后答案应该减去1
- 在处理这种二位数组时,可以构建一个
move[]数组用来表示向前后左右四个方向递进
/**
* 时间复杂度:O(m * n) 每个格子都会过一遍
* 空间复杂度:O(m * n) 队列的最大值
*/
class Solution {
public int maxDistance(int[][] grid) {
int[][] move = {
{
0, 1}, {
0, -1}, {
-1, 0}, {
1, 0},
};
int m = grid.length, n = grid[0].length;
LinkedList<int[]> queue = new LinkedList<>();
// 将陆地加入队列
for(int i = 0; i < m; i++)
for(int j = 0; j < n; j++)
if(grid[i][j] == 1) queue.offer(new int[] {
i, j});
if(queue.isEmpty() || queue.size() == m * n) return -1;
int[] point = null;
int curX = 0, curY = 0, newX = 0, newY = 0;
while(!queue.isEmpty()){
point = queue.poll();
curX = point[0];
curY = point[1];
for(int i = 0; i < 4; i++) {
newX = curX + move[i][0];
newY = curY + move[i][1];
if(newX < 0 || newX >= m || newY < 0
|| newY >= n || grid[newX][newY] != 0)
continue;
// 对走过的路进行标记,这里是标记层数
grid[newX][newY] = grid[curX][curY] + 1;
queue.offer(new int[] {
newX, newY});
}
}
return grid[point[0]][point[1]] - 1;
}
}
026、LeetCode1255-得分最高的单词集合(dfs,回溯)
- 本题目存在限制条件
1 <= words.length <= 14,所以我们可以使用全排列,也就是对words中全部的字符串选或不选,找出所有的情况。 - 于是使用dfs加回溯的算法,为了方便本题目,构造了
scores[]数组,scores[i]代表words[i]单词的得分。 - 为了方便本题目,构造了
letterCnt[]数组,letterCnt[i]代表第i个字符(a为0,b为1…)的数量 - 于是在递归中回溯,不断更新最大值
/**
* 时间复杂度:O(2^n) 每个单词都有选和不选两种情况,n为单词的数量
* 空间复杂度:O(n) 递归栈的深度,n为words中单词的数量
*/
class Solution {
private int maxScore = 0;
public int maxScoreWords(String[] words, char[] letters, int[] score) {
int[] scores = new int[words.length];
int[] letterCnt = new int[26];
for(char ch : letters)
letterCnt[ch - 'a']++;
for(int i = 0; i < words.length; i++)
for(int j = 0; j < words[i].length(); j++)
scores[i] += score[words[i].charAt(j) - 'a'];
backTracking(0, 0, words, letterCnt, scores);
return maxScore;
}
public void backTracking(int start, int curScore, String[] words, int[] letterCnt, int[] scores) {
// 如果当前的score大于最大值,就更新最大值
if(curScore > maxScore) maxScore = curScore;
for(int i = start; i < words.length; i++){
boolean valid = true;
for(int j = 0; j < words[i].length(); j++) {
// 只要出现一个字母不够用了,就不合法,下面就不往下递归
if(--letterCnt[words[i].charAt(j) - 'a'] < 0) valid = false;
}
if(valid) {
// 如果减去字母之后发现不够了,就不往下递归了
backTracking(i + 1, curScore + scores[i], words, letterCnt, scores);
}
// 有没有往下递归都需要将原状态恢复
for(int j = 0; j < words[i].length(); j++) {
letterCnt[words[i].charAt(j) - 'a']++;
}
}
}
}
027、LeetCode1584-连接所有点的最小费用(prim、Kruskal)
本题目是图论算法中最小生成树的解法,比较经典的解法有:kruskal算法、prim算法。需要记住
两种问题可以解决,值得注意的是:kruskal算法中需要使用到并查集的数据结构
kruskal算法:
class Solution {
// Kruskal
public int minCostConnectPoints(int[][] points) {
List<Edge> edges = new ArrayList<>();
for(int i = 0; i < points.length; i++) {
for(int j = i; j < points.length; j++) {
edges.add(new Edge(i, j, getLength(points, i, j)));
}
}
Collections.sort(edges, (a, b) -> (
a.len - b.len
));
int ans = 0, edgeNum = 0;
DSU dsu = new DSU(points.length);
for(Edge edge : edges) {
if(dsu.union(edge.point1, edge.point2)){
ans += edge.len;
edgeNum++;
}
if(edgeNum == points.length - 1) break;
}
return ans;
}
// 两个点之间的曼哈顿距离
public int getLength(int[][] points, int point1, int point2) {
return Math.abs(points[point1][0] - points[point2][0]) +
Math.abs(points[point1][1] - points[point2][1]);
}
// 边类
private class Edge{
int point1;
int point2;
int len;
Edge(int point1, int point2, int len) {
this.point1 = point1;
this.point2 = point2;
this.len = len;
}
}
// 并查集模板
class DSU{
}
}
prim算法:
class Solution {
public int minCostConnectPoints(int[][] points) {
return prim(points);
}
/**
* 图论中的最小生成树Prim算法
* @param points
* @return
*/
public int prim(int[][] points){
int res = 0;
//1.构造邻接矩阵
int len = points.length;
int[][] dp = new int[len][len]; // dp[0][1] 表示下标为0 到 下标为1 的 曼哈顿值
for (int i = 0; i < len; i++) {
for (int j = i; j < len; j++) {
if(i == j){
dp[i][j] = 0;
}else {
dp[i][j] = computeConst(points[i][0],points[i][1],points[j][0],points[j][1]);
dp[j][i] = computeConst(points[i][0],points[i][1],points[j][0],points[j][1]);
}
}
}
// v_new 表示图中节点的访问情况,最开始全部为-1,表示未加入到v_new中,若某节点加入到了v_new中, 则将其置为0
int[] v_new = new int[len];
// lowcost 保存每个节点离v_new中所有节点的最短距离。初始化为Integer.MAX_VALUE,如果节点已经加入到了v_new中,则置为-1
int[] lowcost = new int[len];
for (int i = 0; i < len; i++) {
v_new[i] = -1;
lowcost[i] = Integer.MAX_VALUE;
}
//2.随机选取一个节点,默认为第一个节点,并且更新lowcost里面的值
v_new[0] = 0;
for (int i = 0; i < len; i++) {
if(i == 0){
continue;
}else {
lowcost[i] = dp[0][i];
}
}
//3. 遍历未放入v_new 的剩余的节点,
for (int i = 1; i < len; i++) {
// 找到图中离 v_new 最近的点
int minIdx = -1; // minIdx 表示找到节点的下标
int minVal = Integer.MAX_VALUE; // minVal 表示找到节点的下标对应的值
for (int j = 0; j < len; j++) {
if(lowcost[j] < minVal){
minIdx = j;
minVal = lowcost[j];
}
}
//更新 v_new 里面的值
res += minVal;
v_new[minIdx] = 0;
lowcost[minIdx] = Integer.MAX_VALUE;
//更新 lowcost 里面的值
for (int j = 0; j < len; j++) {
if (v_new[j] == -1 && dp[j][minIdx] < lowcost[j]){
lowcost[j] = dp[j][minIdx];
}
}
}
return res;
}
private int computeConst(int x1, int y1, int x2,int y2){
return Math.abs(x1 - x2) + Math.abs(y1 - y2);
}
}
028、LeetCode301-删除无效的括号(BFS)
BFS / DFS: 通过穷尽所有的可能来找到符合条件的解或者解的个数
本题目可以使用dfs和bfs,就理解来说,bfs较为简单。
bfs和dfs是图论中衍生出来的算法思想,当不局限于树和图数据结构之外,在其他地方使用dfs和bfs情况一般是这样:
- BFS:BFS是面,每一层的节点同时进行搜索,一般借助于队列这种数据结构
- DFS: DFS 是线,纵向一个一个解决,可以衍生出来回溯、剪枝的思想,一般要借助递归或者栈来进行。
class Solution:
def removeInvalidParentheses(self, s:str) -> List[str]:
def isValid(s:str) -> bool:
cnt = 0
for c in s:
if c == "(": cnt += 1
elif c == ")": cnt -= 1
if cnt < 0: return False # 只用中途cnt出现了负值,你就要终止循环,已经出现非法字符了
return cnt == 0
# BFS
level = {
s} # 用set避免重复
while True:
valid = list(filter(isValid, level)) # 所有合法字符都筛选出来
if valid: return valid # 如果当前valid是非空的,说明已经有合法的产生了
# 下一层level
next_level = set()
for item in level:
for i in range(len(item)):
if item[i] in "()": # 如果item[i]这个char是个括号就删了,如果不是括号就留着
next_level.add(item[:i]+item[i+1:])
level = next_level
029、LeetCode322-零钱兑换(背包,dp)
比较典型的动态规划问题。
假设 f(n) 代表要凑齐金额为 n 所要用的最少硬币数量,那么有:
// 这里的 +1 不是指 "取一次当前面额" ,而是指的"取了这个行为"
// 因为即使 "取很多次",也是需要"从取一次开始的"
// 即 f()里面可能也取了多次,只不过遍历所有的金额可以"囊括所有情况"
f(n) = min(f(n - c1), f(n - c2), ... f(n - cn)) + 1
其中 c1 ~ cn 为硬币的所有面额。再具体解释一下这个公式吧,例如这个示例:
输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1
题目求的值为 f(11),第一次选择硬币时我们有三种选择。
假设我们取面额为 1 的硬币,那么接下来需要凑齐的总金额变为 11 - 1 = 10,即 f(11) = f(10) + 1,这里的 +1 就是我们取出的面额为 1 的硬币。
同理,如果取面额为 2 或面额为 5 的硬币可以得到:
f(11) = f(9) + 1f(11) = f(6) + 1
所以:
f(11) = min(f(10), f(9), f(6)) + 1
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
if amount < 0: return -1
# 找零数量不会超过amount
res = [0] + [amount+1] * amount
for i in range(1, len(res)):
for coin in coins:
if i < coin: continue
res[i] = min(res[i], 1 + res[i - coin])
return res[-1] if res[-1] != amount + 1 else -1
030、LeetCode518-零钱兑换2(背包,dp)
和上一道题搭配食用,本题目求的是"可以凑成总金额的硬币组合数"
- dp数组代表的意思是,dp[i]:凑成i所需要的硬币最小值
- 状态转移公式为:
dp[j] = dp[j] + dp[j - coins[i]],意思是**不取当前硬币的所有情况(dp[j-1]) + 取当前硬币的所有组合数(dp[j - coins[i]]) ** - 用滚动数组将二位数组一维化
/**
* 时间复杂度:O(m * n) m为amount的大小,n为硬币数组的长度
* 空间复杂度:O(m)
*/
class Solution {
public int change(int amount, int[] coins) {
int dp[] = new int[amount+1];
dp[0] = 1;
for (int coin : coins) {
for (int j = 1; j <= amount; j++) {
if (j >= coin) {
dp[j] = dp[j] + dp[j - coin];
}
}
}
return dp[amount];
}
}
031、LeetCode959-由斜杠划分区域(并查集)
读完题目后我们发现整体需要归类,好像是可以使用并查集,但是完全不知道如何使用。
不难发现,「斜杠」、「反斜杠」把单元格拆分成的 2 个三角形的形态,在做合并的时候需要分类讨论。
根据「斜杠」、「反斜杠」分割的特点,我们把一个单元格分割成逻辑上的 4 个部分。:
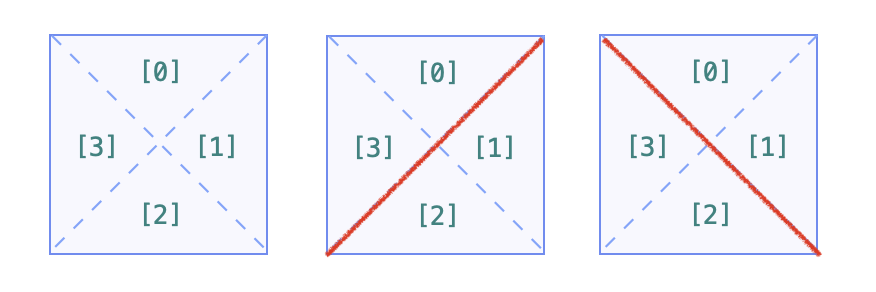
我们须要遍历一次输入的二维网格 grid,在 单元格内 和 单元格间 进行合并。
单元格内:
-
如果是空格:合并 0、1、2、3;
-
如果是斜杠:合并 0、3,合并 1、2;
-
如果是反斜杠:合并 0、1,合并 2、3。
单元格间:
把每一个单元格拆分成 4 个小三角形以后,相邻的单元格须要合并,无须分类讨论。我们选择在遍历 grid 的每一个单元格的时候,分别「向右、向下」尝试合并。
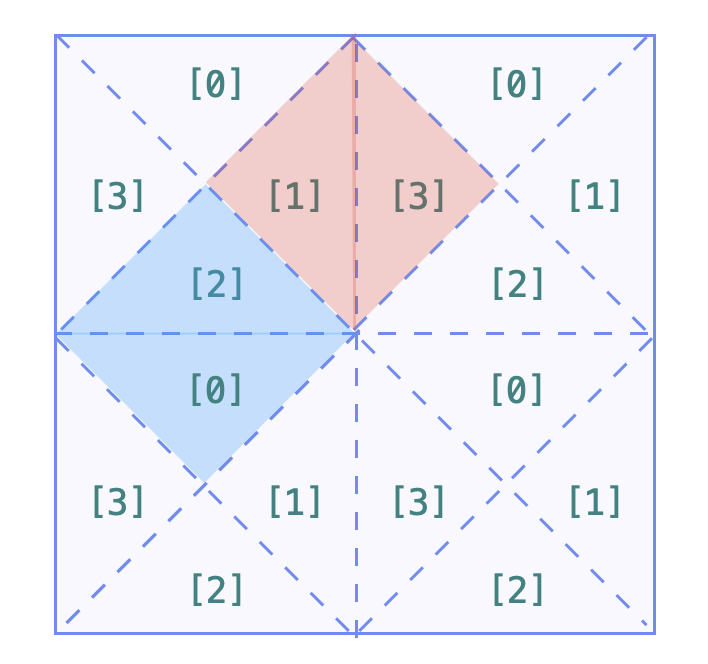
- 向右:合并 1 (当前单元格)和 3(当前单元格右边 1 列的单元格),上图中红色部分;
- 向下:合并 2 (当前单元格)和 0(当前单元格下边 1 列的单元格),上图中蓝色部分。
/**
* 时间复杂度:O(n^2 logn) n为网格长度,logn是一次union操作
* 空间复杂度:O(n^2) 并查集大小
*/
class Solution {
public int regionsBySlashes(String[] grid) {
int N = grid.length;
int size = 4 * N * N;
DSU dsu = new DSU(size);
for(int i = 0; i < grid.length; i++) {
String str = grid[i];
int count = 0;
for(int j = 0; j < str.length(); j++) {
int index0 = N * i * 4 + count * 4, index1 = index0 + 1;
int index2 = index0 + 2, index3 = index0 + 3;
if(str.charAt(j) == ' ') {
dsu.union(index0, index1);
dsu.union(index1, index2);
dsu.union(index2, index3);
} else if(str.charAt(j) == '/') {
dsu.union(index0, index1);
dsu.union(index2, index3);
} else {
dsu.union(index0, index2);
dsu.union(index1, index3);
}
count++;
if(count != N) dsu.union(index2, index2 + 3);
if(i != grid.length - 1) dsu.union(index3, index3 + N * 4 - 3);
}
}
int ans = 0;
for(int i = 0; i < dsu.p.length; i++) {
if(i == dsu.p[i]) ans++;
}
return ans;
}
}
032、LeetCode338-比特位计数(位运算,dp)
- 求 n 的二进制有几个1,可以看一下**
n >> 1有几个1,然后再看最后有一个是不是1** res[i] = res[res >> 1] + (i & 1)
class Solution {
public int[] countBits(int num) {
int[] res = new int[num + 1];
for(int i = 0; i < res.length; i++) {
res[i] = res[res >>1] + (1 & i);
}
return res;
}
}
第二种方法是:
- 去除二进制 i 的最后一个1,该数一定比 i 小:
i & (i - 1) - 所以
res[i] = res[i &(i-1)] + 1
class Solution {
public int[] countBits(int num) {
int[] res = new int[num + 1];
for(int i = 0; i < res.length; i++) {
res[i] = res[i & (i-1)] + 1;
}
return res;
}
}
032、LeetCode338-比特位计数(位运算,dp)
- 求 n 的二进制有几个1,可以看一下**
n >> 1有几个1,然后再看最后有一个是不是1** res[i] = res[res >> 1] + (i & 1)
class Solution {
public int[] countBits(int num) {
int[] res = new int[num + 1];
for(int i = 0; i < res.length; i++) {
res[i] = res[res >>1] + (1 & i);
}
return res;
}
}
第二种方法是:
- 去除二进制 i 的最后一个1,该数一定比 i 小:
i & (i - 1) - 所以
res[i] = res[i &(i-1)] + 1
class Solution {
public int[] countBits(int num) {
int[] res = new int[num + 1];
for(int i = 0; i < res.length; i++) {
res[i] = res[i & (i-1)] + 1;
}
return res;
}
}