学习代码来源于:遗传算法python
一.主要思想
遗传算法是根据达尔文的“适者生存,优胜劣汰”的思想来找到最优解的额,其特点是所找到的解是全局最优解,相对于蚁群算法可能出现的局部最优解还是有优势的。
二.主要名词
个体(染色体):一个染色体代表一个具体问题的一个解,一个染色体包含若干基因。
基因:一个基因代表具体问题解的一个决策变量。种群:多个个体(染色体)构成一个种群。即一个问题的多组解构成了解的种群。
我们的目的就是让种群中”优胜劣汰“,最终只剩下一个最优解。接下来介绍最基本遗传算法,只用了选择,交叉,变异三种遗传算子。
三.主要步骤
1)种群初始化。我们需要首先通过随机生成的方式来创造一个种群,一般该种群的数量为100~500,这里我们采用二进制将一个染色体(解)编码为基因型。随后用进制转化,将二进制的基因型转化成十进制的表现型。
2)适应度计算(种群评估)。这里我们直接将目标函数值作为个体的适应度。
3)选择(复制)操作。根据种群中个体的适应度大小,通过轮盘赌等方式将适应度高的个体从当前种群中选择出来。其中轮盘赌即是与适应度成正比的概率来确定各个个体遗传到下一代群体中的数量。

具体步骤如下:
(1)首先计算出所有个体的适应度总和Σfi。
(2)其次计算出每个个体的相对适应度大小fi/Σfi,类似于softmax。
(3)再产生一个0到1之间的随机数,依据随机数出现在上述哪个概率区域内来确定各个个体被选中的次数。
4)交叉(交配)运算。该步骤是遗传算法中产生新的个体的主要操作过程,它用一定的交配概率阈值(pc,一般是0.4到0.99)来控制是否采取单点交叉,多点交叉等方式生成新的交叉个体。
具体步骤如下:
(1)先对群体随机配对。
(2)再随机设定交叉点的位置。
(3)再互换配对染色体间的部分基因。
5)变异运算。该步骤是产生新的个体的另一种操作。一般先随机产生变异点,再根据变异概率阈值(pm,一般是0.0001到0.1)将变异点的原有基因取反。
6)终止判断。如果满足条件(迭代次数,一般是200~500)则终止算法,否则返回step2。
四.代码实现
1.种群初始化
(1)随机生成若干个数的二进制染色体。
# -*-coding:utf-8 -*-
#目标求解2*sin(x)+cos(x)最大值
import random
import math
import matplotlib.pyplot as plt
#初始化生成chromosome_length大小的population_size个个体的二进制基因型种群
def species_origin(population_size,chromosome_length):
population=[[]]
#二维列表,包含染色体和基因
for i in range(population_size):
temporary=[]
#染色体暂存器
for j in range(chromosome_length):
temporary.append(random.randint(0,1))
#随机产生一个染色体,由二进制数组成
population.append(temporary)
#将染色体添加到种群中
return population[1:]
# 将种群返回,种群是个二维数组,个体和染色体两维(2)编码
将二进制的染色体基因型编码成十进制的表现型。
#从二进制到十进制
#input:种群,染色体长度
def translation(population,chromosome_length):
temporary=[]
for i in range(len(population)):
total=0
for j in range(chromosome_length):
total+=population[i][j]*(math.pow(2,j))
#从第一个基因开始,每位对2求幂,再求和
# 如:0101 转成十进制为:1 * 20 + 0 * 21 + 1 * 22 + 0 * 23 = 1 + 0 + 4 + 0 = 5
temporary.append(total)
#一个染色体编码完成,由一个二进制数编码为一个十进制数
return temporary
# 返回种群中所有个体编码完成后的十进制数2.适应度计算
个体适应度与其对应的个体表现型x的目标函数值相关联,x越接近于目标函数的最优点,其适应度越大,从而其存活的概率越大。反之适应度越小,存活概率越小。这就引出一个问题关于适应度函数的选择,本例中,函数值总取非负值(删去了。。。),以函数最大值为优化目标,故直接将目标函数作为适应度函数。这里我们直接将目标函数2*sin(x)+cos作为个体适应度。如果,你想优化的是多元函数的话,需要将个体中基因型的每个变量提取出来,分别带入目标函数。比如说:我们想求x1+lnx2的最大值。基因编码为4位编码,其中前两位是x1,后两位是x2。那么我们在求适应度的时候,需要将这两个值分别带入f(x1)=x,f(x2)=lnx。再对f(x1)和f(x2)求和得到此个体的适应度,具体的在此篇中有详解。在本篇中,虽然染色体长度为10,但是实际上只有一个变量。
# 目标函数相当于环境 对染色体进行筛选,这里是2*sin(x)+cos(x)
def function(population,chromosome_length,max_value):
temporary=[]
function1=[]
temporary=translation(population,chromosome_length)
# 暂存种群中的所有的染色体(十进制)
for i in range(len(temporary)):
x=temporary[i]*max_value/(math.pow(2,chromosome_length)-1)
#一个基因代表一个决策变量,其算法是先转化成十进制,然后再除以2的基因个数次方减1(固定值)。
function1.append(2*math.sin(x)+math.cos(x))
#这里将2*sin(x)+cos(x)作为目标函数,也是适应度函数
return function1关于这里的x的生成方式,据资料说只是一个编码规则。于是,我对其进行了几种实验。
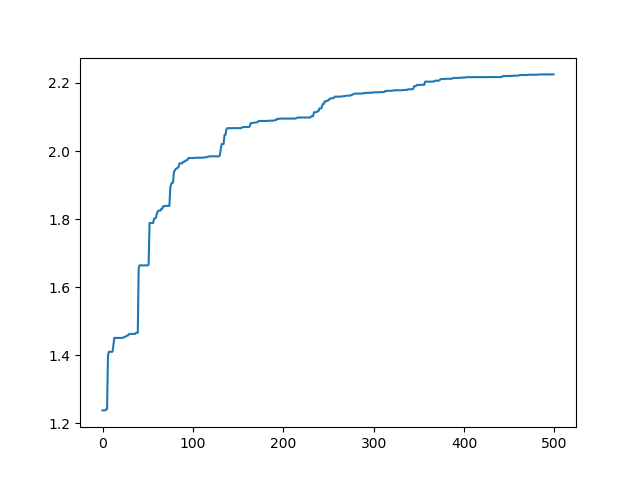
如下,这种是删了max_value的输出结果:
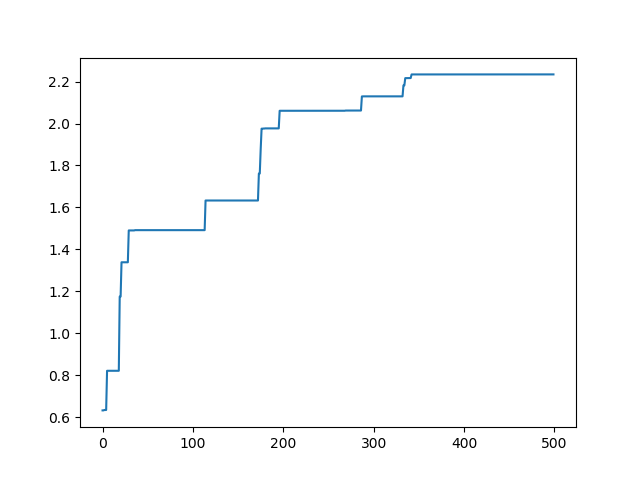
这种少了除号后面的结果:
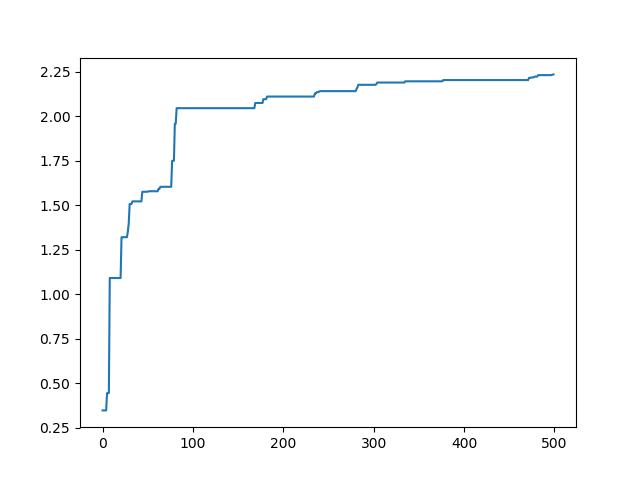
这种是只保留temporay[i]的结果:
从以上结果我们可以看出,这几种结果对最后的优化结果都没有什么影响。但是对其优化速度和平滑性都有影响。这也正是适应度函数选择的意义,选的好的话就可以加快优化效果。
补充:2018.6.16
由下面的选择操作可知,适应度是选择操作的主要参考依据,适应度函数(Fitness Function)的选取直接影响到遗传算法的收敛速度以及能否找到最优解。因而适应度函数的选择问题在遗传算法中是一项很值得研究的课题。一般情况下,关于适应度与目标函数的选择有以下这两种关系:
也就是说,我们要在每一轮迭代(进化)时,要将所有个体的适应度函数值都要遍历,然后得到最/大小值。此时每一轮的适应度函数都是在变化的。之前,我们程序中的个体适应度函数是不变化的。实际上要得到更准确的结果,除了以上基本变化,还有以下的适应度变化方法:
我们对个体的适应度调整的目的有两个:
一是维持个体之间的合理差距,加速竞争。
二是避免个体之间的差距过大,限制竞争。
此外,还有适应度共享等调节方式,此处不再赘述。来自于,选择和适应度函数。
另外,在这段程序中,采用一种巧妙的方式限定了表现型的大小。比如,我们这里限制最大值为30,基因长度为6,则30/(2**6-1)=0.47,我们这里取一个表现型的最大值-2**6=64,则64*0.47=30.47,大致(这个词..有点不好意思说出来)符合我们的限制范围。
3.选择操作
(1).只保留非负值的适应度/函数值(不小于0)
def fitness(function1):
fitness1=[]
min_fitness=mf=0
for i in range(len(function1)):
if(function1[i]+mf>0):
temporary=mf+function1[i]
else:
temporary=0.0
# 如果适应度小于0,则定为0
fitness1.append(temporary)
#将适应度添加到列表中
return fitness1(2).首先计算出所有个体的适应度总和Σfi
#计算适应度和
def sum(fitness1):
total=0
for i in range(len(fitness1)):
total+=fitness1[i]
return total
#计算适应度斐波纳挈列表,这里是为了求出累积的适应度
def cumsum(fitness1):
for i in range(len(fitness1)-2,-1,-1):
# range(start,stop,[step])
# 倒计数
total=0
j=0
while(j<=i):
total+=fitness1[j]
j+=1
#这里是为了将适应度划分成区间
fitness1[i]=total
fitness1[len(fitness1)-1]=1(3).再产生一个0到1之间的随机数,依据随机数出现在上述哪个概率区域内来确定各个个体被选中的次数。
#3.选择种群中个体适应度最大的个体
def selection(population,fitness1):
new_fitness=[]
#单个公式暂存器
total_fitness=sum(fitness1)
#将所有的适应度求和
for i in range(len(fitness1)):
new_fitness.append(fitness1[i]/total_fitness)
#将所有个体的适应度概率化,类似于softmax
cumsum(new_fitness)
#将所有个体的适应度划分成区间
ms=[]
#存活的种群
population_length=pop_len=len(population)
#求出种群长度
#根据随机数确定哪几个能存活
for i in range(pop_len):
ms.append(random.random())
# 产生种群个数的随机值
ms.sort()
# 存活的种群排序
fitin=0
newin=0
new_population=new_pop=population
#轮盘赌方式
while newin<pop_len:
if(ms[newin]<new_fitness[fitin]):
new_pop[newin]=pop[fitin]
newin+=1
else:
fitin+=1
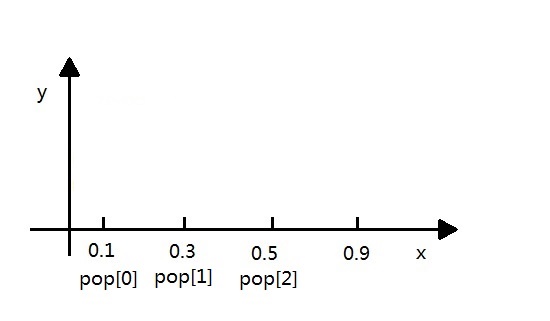
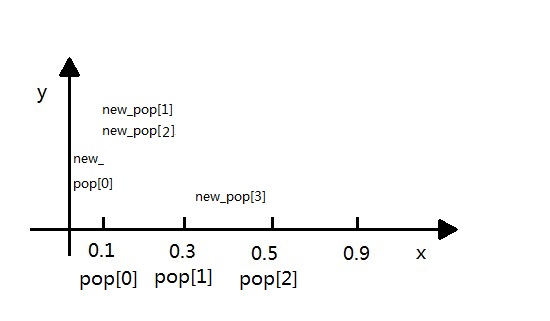
population=new_pop这里需要详细解释一下轮盘赌算法,其实就是典型的几何概率问题.这里根据cumsum函数将个体的适应度[0.1,0.2,0.2,0.4.....]都划分成区间[0.1,0.3,0.5,0.9...],如下图:
然后,random产生的ms[]排序后为[0.08,0.12,0.15,0.4.....],就有如下的程序:
我们可以看出新的种群是如下分布的:
这意味着某个体适应度越大,新的种群中该个体数量越多。
4.交叉
def crossover(population,pc):
#pc是概率阈值,选择单点交叉还是多点交叉,生成新的交叉个体,这里没用
pop_len=len(population)
for i in range(pop_len-1):
cpoint=random.randint(0,len(population[0]))
#在种群个数内随机生成单点交叉点
temporary1=[]
temporary2=[]
temporary1.extend(pop[i][0:cpoint])
temporary1.extend(pop[i+1][cpoint:len(population[i])])
#将tmporary1作为暂存器,暂时存放第i个染色体中的前0到cpoint个基因,
#然后再把第i+1个染色体中的后cpoint到第i个染色体中的基因个数,补充到temporary2后面
temporary2.extend(pop[i+1][0:cpoint])
temporary2.extend(pop[i][cpoint:len(pop[i])])
# 将tmporary2作为暂存器,暂时存放第i+1个染色体中的前0到cpoint个基因,
# 然后再把第i个染色体中的后cpoint到第i个染色体中的基因个数,补充到temporary2后面
pop[i]=temporary1
pop[i+1]=temporary2
# 第i个染色体和第i+1个染色体基因重组/交叉完成5.变异
#step4:突变
def mutation(population,pm):
# pm是概率阈值
px=len(population)
# 求出种群中所有种群/个体的个数
py=len(population[0])
# 染色体/个体中基因的个数
for i in range(px):
if(random.random()<pm):
#如果小于阈值就变异
mpoint=random.randint(0,py-1)
# 生成0到py-1的随机数
if(population[i][mpoint]==1):
#将mpoint个基因进行单点随机变异,变为0或者1
population[i][mpoint]=0
else:
population[i][mpoint]=16.其他
# 将每一个染色体都转化成十进制 max_value为基因最大值,为了后面画图用
def b2d(b,max_value,chromosome_length):
total=0
for i in range(len(b)):
total=total+b[i]*math.pow(2,i)
#从第一位开始,每一位对2求幂,然后求和,得到十进制数?
total=total*max_value/(math.pow(2,chromosome_length)-1)
return total
#寻找最好的适应度和个体
def best(population,fitness1):
px=len(population)
bestindividual=[]
bestfitness=fitness1[0]
for i in range(1,px):
# 循环找出最大的适应度,适应度最大的也就是最好的个体
if(fitness1[i]>bestfitness):
bestfitness=fitness1[i]
bestindividual=population[i]
return [bestindividual,bestfitness]7.主程序
population_size=500
max_value=10
# 基因中允许出现的最大值
chromosome_length=10
pc=0.6
pm=0.01
results=[[]]
fitness1=[]
fitmean=[]
population=pop=species_origin(population_size,chromosome_length)
#生成一个初始的种群
for i in range(population_size):#注意这里是迭代500次
function1=function(population,chromosome_length,max_value)
fitness1=fitness(function1)
best_individual,best_fitness=best(population,fitness1)
results.append([best_fitness,b2d(best_individual,max_value,chromosome_length)])
#将最好的个体和最好的适应度保存,并将最好的个体转成十进制
selection(population,fitness1)#选择
crossover(population,pc)#交配
mutation(population,pm)#变异
results=results[1:]
results.sort()
X=[]
Y=[]
for i in range(500):#500轮的结果
X.append(i)
Y.append(results[i][0])
plt.plot(X,Y)
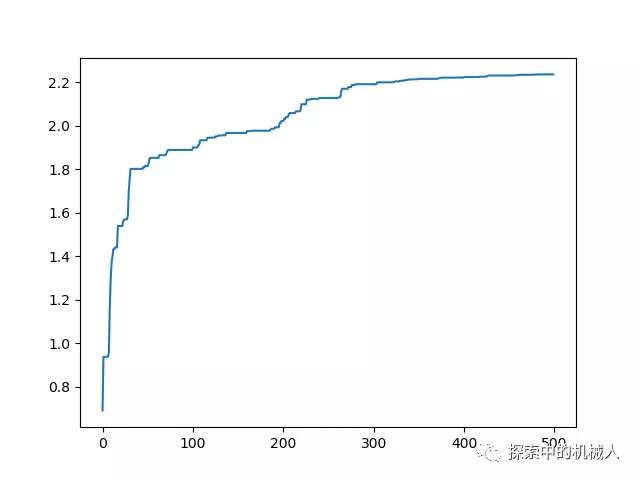
plt.show()8.迭代结果
我们可以看到最后经过500轮的迭代后,其结果已经非常接近2.2了。
9.完整代码
# -*-coding:utf-8 -*-
#目标求解2*sin(x)+cos(x)最大值
import random
import math
import matplotlib.pyplot as plt
class GA(object):
#初始化种群 生成chromosome_length大小的population_size个个体的种群
def __init__(self,population_size,chromosome_length,max_value,pc,pm):
self.population_size=population_size
self.choromosome_length=chromosome_length
# self.population=[[]]
self.max_value=max_value
self.pc=pc
self.pm=pm
# self.fitness_value=[]
def species_origin(self):
population=[[]]
for i in range(self.population_size):
temporary=[]
#染色体暂存器
for j in range(self.choromosome_length):
temporary.append(random.randint(0,1))
#随机产生一个染色体,由二进制数组成
population.append(temporary)
#将染色体添加到种群中
return population[1:]
# 将种群返回,种群是个二维数组,个体和染色体两维
#从二进制到十进制
#编码 input:种群,染色体长度 编码过程就是将多元函数转化成一元函数的过程
def translation(self,population):
temporary=[]
for i in range(len(population)):
total=0
for j in range(self.choromosome_length):
total+=population[i][j]*(math.pow(2,j))
#从第一个基因开始,每位对2求幂,再求和
# 如:0101 转成十进制为:1 * 20 + 0 * 21 + 1 * 22 + 0 * 23 = 1 + 0 + 4 + 0 = 5
temporary.append(total)
#一个染色体编码完成,由一个二进制数编码为一个十进制数
return temporary
# 返回种群中所有个体编码完成后的十进制数
#from protein to function,according to its functoin value
#a protein realize its function according its structure
# 目标函数相当于环境 对染色体进行筛选,这里是2*sin(x)+math.cos(x)
def function(self,population):
temporary=[]
function1=[]
temporary=self.translation(population)
for i in range(len(temporary)):
x=temporary[i]*self.max_value/(math.pow(2,self.choromosome_length)-10)
function1.append(2*math.sin(x)+math.cos(x))
#这里将sin(x)作为目标函数
return function1
#定义适应度
def fitness(self,function1):
fitness_value=[]
num=len(function1)
for i in range(num):
if(function1[i]>0):
temporary=function1[i]
else:
temporary=0.0
# 如果适应度小于0,则定为0
fitness_value.append(temporary)
#将适应度添加到列表中
return fitness_value
#计算适应度和
def sum(self,fitness_value):
total=0
for i in range(len(fitness_value)):
total+=fitness_value[i]
return total
#计算适应度斐伯纳且列表
def cumsum(self,fitness1):
for i in range(len(fitness1)-2,-1,-1):
# range(start,stop,[step])
# 倒计数
total=0
j=0
while(j<=i):
total+=fitness1[j]
j+=1
fitness1[i]=total
fitness1[len(fitness1)-1]=1
#3.选择种群中个体适应度最大的个体
def selection(self,population,fitness_value):
new_fitness=[]
#单个公式暂存器
total_fitness=self.sum(fitness_value)
#将所有的适应度求和
for i in range(len(fitness_value)):
new_fitness.append(fitness_value[i]/total_fitness)
#将所有个体的适应度正则化
self.cumsum(new_fitness)
#
ms=[]
#存活的种群
population_length=pop_len=len(population)
#求出种群长度
#根据随机数确定哪几个能存活
for i in range(pop_len):
ms.append(random.random())
# 产生种群个数的随机值
# ms.sort()
# 存活的种群排序
fitin=0
newin=0
new_population=new_pop=population
#轮盘赌方式
while newin<pop_len:
if(ms[newin]<new_fitness[fitin]):
new_pop[newin]=population[fitin]
newin+=1
else:
fitin+=1
population=new_pop
#4.交叉操作
def crossover(self,population):
#pc是概率阈值,选择单点交叉还是多点交叉,生成新的交叉个体,这里没用
pop_len=len(population)
for i in range(pop_len-1):
if(random.random()<self.pc):
cpoint=random.randint(0,len(population[0]))
#在种群个数内随机生成单点交叉点
temporary1=[]
temporary2=[]
temporary1.extend(population[i][0:cpoint])
temporary1.extend(population[i+1][cpoint:len(population[i])])
#将tmporary1作为暂存器,暂时存放第i个染色体中的前0到cpoint个基因,
#然后再把第i+1个染色体中的后cpoint到第i个染色体中的基因个数,补充到temporary2后面
temporary2.extend(population[i+1][0:cpoint])
temporary2.extend(population[i][cpoint:len(population[i])])
# 将tmporary2作为暂存器,暂时存放第i+1个染色体中的前0到cpoint个基因,
# 然后再把第i个染色体中的后cpoint到第i个染色体中的基因个数,补充到temporary2后面
population[i]=temporary1
population[i+1]=temporary2
# 第i个染色体和第i+1个染色体基因重组/交叉完成
def mutation(self,population):
# pm是概率阈值
px=len(population)
# 求出种群中所有种群/个体的个数
py=len(population[0])
# 染色体/个体基因的个数
for i in range(px):
if(random.random()<self.pm):
mpoint=random.randint(0,py-1)
#
if(population[i][mpoint]==1):
#将mpoint个基因进行单点随机变异,变为0或者1
population[i][mpoint]=0
else:
population[i][mpoint]=1
#transform the binary to decimalism
# 将每一个染色体都转化成十进制 max_value,再筛去过大的值
def b2d(self,best_individual):
total=0
b=len(best_individual)
for i in range(b):
total=total+best_individual[i]*math.pow(2,i)
total=total*self.max_value/(math.pow(2,self.choromosome_length)-1)
return total
#寻找最好的适应度和个体
def best(self,population,fitness_value):
px=len(population)
bestindividual=[]
bestfitness=fitness_value[0]
# print(fitness_value)
for i in range(1,px):
# 循环找出最大的适应度,适应度最大的也就是最好的个体
if(fitness_value[i]>bestfitness):
bestfitness=fitness_value[i]
bestindividual=population[i]
return [bestindividual,bestfitness]
def plot(self, results):
X = []
Y = []
for i in range(500):
X.append(i)
Y.append(results[i][0])
plt.plot(X, Y)
plt.show()
def main(self):
results = [[]]
fitness_value = []
fitmean = []
population = pop = self.species_origin()
for i in range(500):
function_value = self.function(population)
# print('fit funtion_value:',function_value)
fitness_value = self.fitness(function_value)
# print('fitness_value:',fitness_value)
best_individual, best_fitness = self.best(population,fitness_value)
results.append([best_fitness, self.b2d(best_individual)])
# 将最好的个体和最好的适应度保存,并将最好的个体转成十进制,适应度函数
self.selection(population,fitness_value)
self.crossover(population)
self.mutation(population)
results = results[1:]
results.sort()
self.plot(results)
if __name__ == '__main__':
population_size=400
max_value=10
chromosome_length=20
pc=0.6
pm=0.01
ga=GA(population_size,chromosome_length,max_value,pc,pm)
ga.main()