前戏
某房地产公司老板给了小李一份数据是关于公司不同地区不同的房价数据,数据中包括房屋的大小,面积,所处商业位置等信息。而后老板想让小李预测一下在另一个商区的某几套房子的价格大概能卖多少钱。拿到数据后的小李想这我怎么知道具体怎么做呀?不慌,下面介绍如何用Python结合回归模型具体实现。
通用性理论步骤大框架:
探索性数据分析
数据清洗
建模分析
模型评估
01

回归理论简介
利用数据统计原理,对大量统计数据进行数学处理,并确定因变量与某些自变量的相关关系,建立一个相关性较好的回归方程(函数表达式),并加以外推,用于预测今后的因变量的变化的分析方法。
线性回归核心模型简介:
回归方程

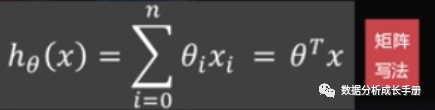
2. 误差方程
由于样本数据不一定全部都在一个直线或者一个平面(二维),必定存在一些误差,误差可表示为如下方程。其中Ɛ是误差项,通常用一个随机变量表示。
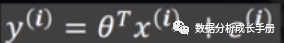
3. 对误差项Ɛ的要求
每一个Ɛ相互独立,其服从均值为0,方差为σ2的正态分布
这里均值为0,意味着Ɛ求和为0
拟合直线不要求完全服从期望值为0的正态分布,但要求尽量趋近

4. 目标函数
根据对误差函数服从高斯分布的假设,可推导出目标函数为如下:
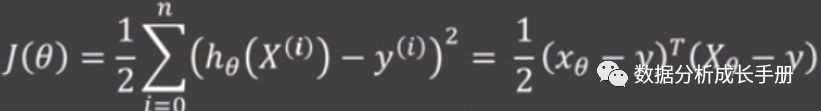
随后求偏导计算偏导为0时的θ。
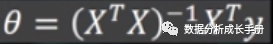
理论说明:
以上是用正规方程的方法来求解优化参数θ,但是有些矩阵是不可求逆的并且求逆运算量很大。后面直接使用梯度下降法来优化参数θ。
02
梯度下降法
机器学习目标函数,一般都是凸函数。而凸函数求解问题,可以把目标损失函数想象成一口锅,一只蚂蚁想从锅上某个点走到锅底。非常直观的想法就是,它沿着初始某个点的函数的梯度方向相反的方向走(即梯度下降)。那决定他何时走到锅底的三个关键问题就是:
走的初始点在哪
走的方向
一步能走多远
这也是梯度下降法的三要素:初始点、下降方向、步长(学习率大小)。
其他关于梯度下降法的内容这里不再描述,配一张几张学习大佬Ng视频课机器学习的插图。
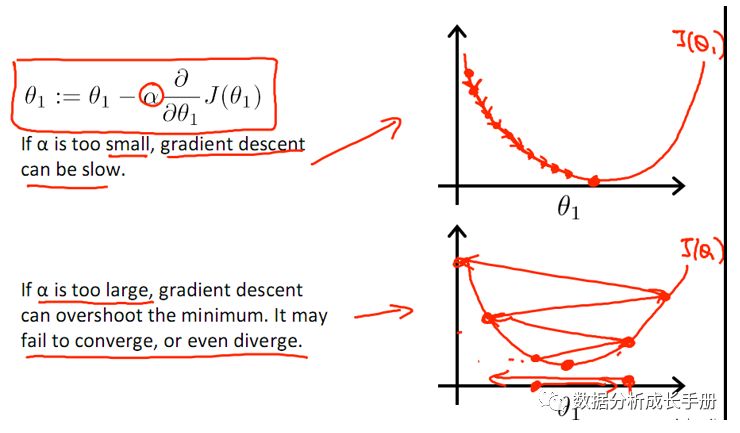
注意点:
梯度下降法是收敛到局部最小值,不一定可以收敛到全局最小。
学习率的大小要适中,太小可能导致收敛太慢,太大可能会导致不收敛
03
模型评估
拿到数据之后,你可能需要首先探索性的分析一下数据的特征(检测特征相关性等)。有些特征之间是高度相关的,如果在特征较多而数据量又很小的情况下将所有特征都拟合模型可能会导致过拟合。这样你可能需要进行降维处理以便得到更加适合于模型的主要特征。但是这些都只是推理,需要找到一种量化方法来评价前后多种模型对问题的解决效果。而针对于回归模型一般用以下几个参数来衡量。
SSE(和方差、误差平方和):The sum of squares due to error
MSE(均方差、方差):Mean squared error
RMSE(均方根、标准差):Root mean squared error
R-square(确定系数) Coefficient of determination
限于篇幅问题,关于以上指标的计算小伙伴们可自行查阅资料简单了解即可。
04
Python实现线性回归实例
利用sklearn简单实现
Python手写梯度下降法实现
借助sklearn实现代码:

不借助工具包sklearn实现:


结果对比:


关注“数据分析成长手册” 回复“回归分析”可获得本文代码数据。
总结:本文介绍了线性回归分析的相关内容和梯度下降法,首先借助sklearn实现线性回归分析,随后利用梯度下降法手写线性回归分析并对比结果。
前两篇文章从探索性数据特征分析[你愿意花十分钟系统了解数据分析方法吗?]到数据清洗等介绍了做挖掘建模前的预处理[你会用Python做数据预处理吗?]工作。
后续文章将展开挖掘建模算法系列打卡,期待每周一到两个机器算法打卡系列更新完常用整套统计数据分析系列的后续基础内容。
----爱德宝器于SCU。