1.主成分分析介绍
主成分分析是一种用于连续属性的数据降维方法,它构造了原始数据的一个正交变换,新空间的基底去除了原始空间基底下数据的相关性,只需使用少量新变量就能够解释原始数据中大部分的变异。在应用中,通常是选出比原始变量个数少,能解释大部分数据中的变量的几个新变量来代替原始变量建模。
2.主成分分析计算步骤


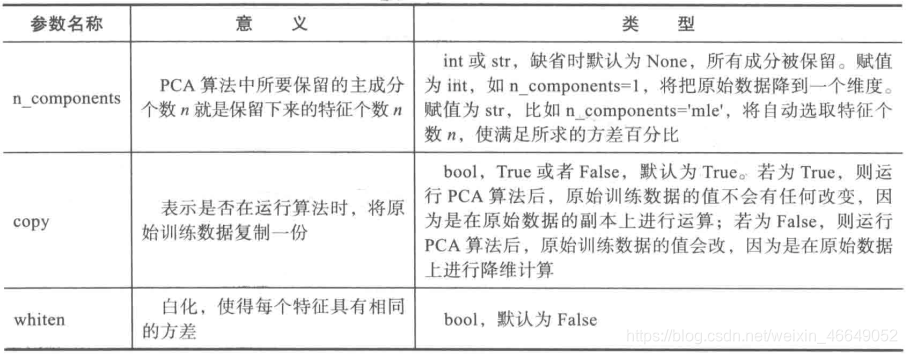
3.PCA常用参数介绍
from sklearn.decomposition import PCA
两个常用属性
components_返回模型的各个特征向量explained_variance_ratio_返回各个成分各自的方差占比(获取各个属性的贡献率)
三个常用方法
fit训练数据transform转换数据inverse_transform逆转换数据
4.PCA实战
from sklearn.decomposition import PCA
import pandas as pd
data = pd.read_excel('data/principal_component.xls',header=None)
pca = PCA()
pca.fit(data)
print(pca.components_) # 返回各模型的特征向量
print(pca.explained_variance_ratio_.cumsum()) # 返回各个成分各自的方差占比
# 发现选取前3个累计贡献率就达到了97%
pca1 = PCA(n_components=3,copy=True,whiten=False)
pca1.fit(data)
low_data = pca1.transform(data) # 降维后的数据
pd.DataFrame(low_data).to_excel('low_data.xls')
pca1.inverse_transform(low_data) # 可以使用inverse_transform函数复原数据
原始数据从8维降到3维,同时这三维数据占了原始数据95%以上的信息。
参考
- 《python数据分析与挖掘实战》
如果对您有帮助,麻烦点赞关注,这真的对我很重要!!!如果需要互关,请评论留言!
