计算机视觉系列教程14：对极几何基本原理图解

教程说明

章号       内容
 0         色彩空间与数字成像(待定)
 1         计算机几何基础
 2         图像增强、滤波、金字塔
 3         图像特征提取
 4         图像特征描述
 5         图像特征匹配
 6         立体视觉

1 导论

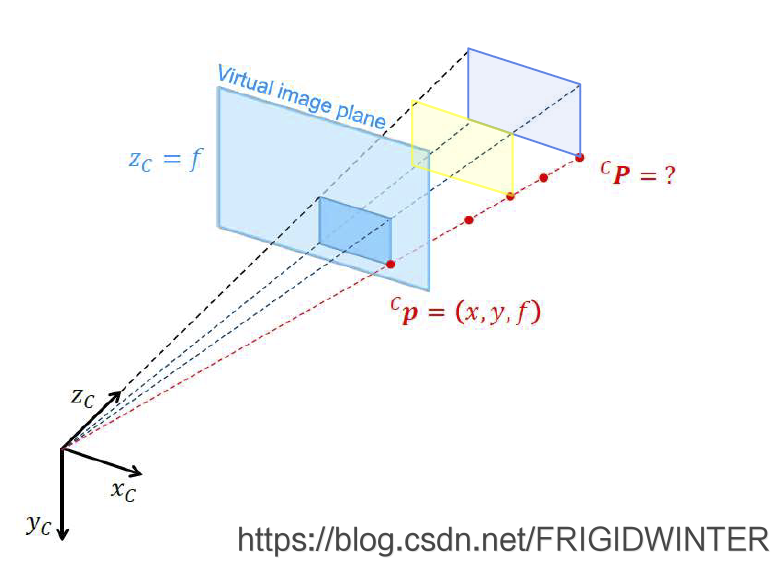
透视几何的缺陷是图像深度信息的丢失，如图1所示，根据相似变换关系，视线上的若干平面都映射为成像面上的一个平面。

图1

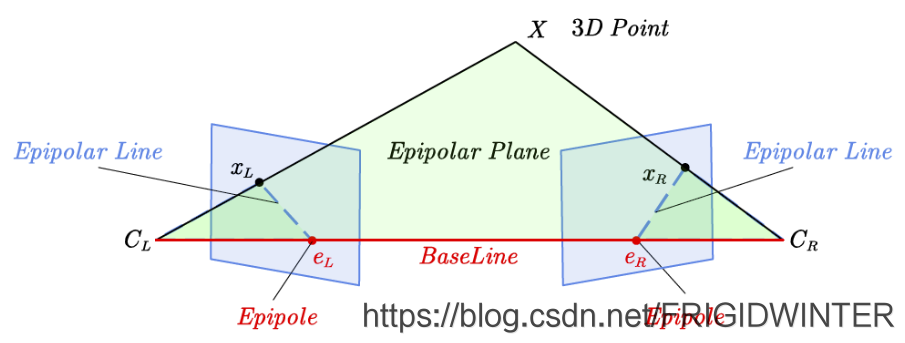
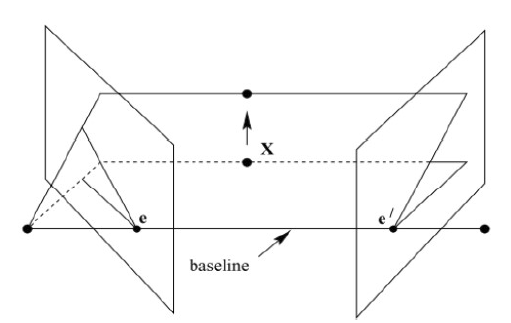
对极几何是两个透视几何模型间的几何约束关系，主要用于实现基于三角测量的双目立体视觉、深度估计等，对极几何约束只能实现点到线的映射，因此约束条件弱于透视几何。图2展示了对极几何的基本概念，其中3D世界的真实点称为物点$X$；物点在相机成像面上形成像点$x_L$、$x_R$；两台透视相机间光心的连线称为基线；基线与成像面的交点称为极点$e_L$、$e_R$，若图像中不存在极点，则说明两个摄像机不能拍摄到彼此；像点与极点的连线称为极线，所有极线相交于极点；透视相机光心与物点确定的平面称为极平面，对于不同物点，极平面绕基线旋转，极线绕极点矩形，如图3所示。

图2

图3(图源网络)

2 对极约束推导

下面讨论两个透视模型间的关系。不妨以左侧相机为参考，设物点${}^{\mathbf{L}}X={\left[\begin{array}{ccc}X& Y& Z\end{array}\right]}^T$，左右两相机间的变换关系为

$${}_{\mathbf{L}}^{\mathbf{R}}\mathbf{T}=\left[\begin{array}{cc}\mathbf{R}& \mathbf{t}\\ 0& 1\end{array}\right]$$

则物点在右透视相机坐标系里的3D坐标为

$${}^{\mathbf{R}}\mathbf{X}{=}_{\mathbf{L}}^{\mathbf{R}}{\mathbf{T}}^{\mathbf{L}}\mathbf{X}=\mathbf{R}\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]+\mathbf{t}=\left[\begin{array}{c}{X}^{\prime }\\ Y^{\prime }\\ Z^{\prime }\end{array}\right]$$

事实上，向量$t$与成像面的交点即为极点。

根据相似关系，物点在左、右成像面上几何坐标为
$$\{\begin{array}{l}{x}_L=f_L\frac{X}{Z}\\ y_L=f_L\frac{Y}{Z}\\ z_L=f_L\end{array}{\Rightarrow }^{\mathbf{L}}\mathbf{x}=\frac{f_L}{Z}{}^{\mathbf{L}}\mathbf{X}\{\begin{array}{l}{x}_R=f_R\frac{X^{\prime }}{Z^{\prime }}\\ y_R=f_R\frac{Y^{\prime }}{Z^{\prime }}\\ z_R=f_R\end{array}{\Rightarrow }^{\mathbf{R}}\mathbf{x}=\frac{f_R}{Z^{\prime }}{}^{\mathbf{R}}\mathbf{X}$$

结合齐次变换关系，有

$$\begin{gathered} {}^{\mathbf{R}}\mathbf{x}=\frac{f_R}{Z^{\prime }}\left({\mathbf{R}}^{\mathbf{L}}\mathbf{X}+\mathbf{t}\right) \\ =\frac{f_R}{Z^{\prime }}\left(\mathbf{R}\frac{Z}{f_L}{\cdot }^{\mathbf{L}}\mathbf{x}+\mathbf{t}\right) \\ =\alpha {\mathbf{R}}^{\mathbf{L}}\mathbf{x}+\beta \mathbf{t} \end{gathered}$$

其中$\alpha$、$\beta$为两个与尺度有关的常数。将等式两边同时与向量$t$做外积，有

$${}^{\mathbf{R}}\mathbf{x}\times \mathbf{t}=\left(\alpha {\mathbf{R}}^{\mathbf{L}}\mathbf{x}+\beta \mathbf{t}\right)\times \mathbf{t}$$

线性化为

$${{\mathbf{t}}^{\wedge }}^{\mathbf{R}}\mathbf{x}=\alpha {\mathbf{t}}^{\wedge }{\mathbf{R}}^{\mathbf{L}}\mathbf{x}$$

两边同乘${}^{\mathbf{R}}{\mathbf{x}}^T$，考虑到${}^{\mathbf{R}}{\mathbf{x}}^T$与向量${}^{\mathbf{R}}\mathbf{x}\times \mathbf{t}$垂直，故

$${\alpha }^{\mathbf{R}}{\mathbf{x}}^T{\mathbf{t}}^{\wedge }{\mathbf{R}}^{\mathbf{L}}\mathbf{x}=0$$

消去常数$\alpha$，即得

$${}^{\mathbf{R}}{\mathbf{x}}^T{\mathbf{E}}^{\mathbf{L}}\mathbf{x}=0$$

其中$\mathbf{E}={\mathbf{t}}^{\wedge }\mathbf{R}$称为本征矩阵(Essential Matrix)，表征了同一物点在两个透视相机成像面上像点的几何约束关系。
下面引入相机内参矩阵，将像点映射到像素平面

$$\{\begin{array}{l}{}^{\mathbf{L}}\mathbf{u}={{\mathbf{K}}_{\mathbf{L}}}^{\mathbf{L}}\mathbf{x}\\ {}^{\mathbf{R}}\mathbf{u}={{\mathbf{K}}_{\mathbf{R}}}^{\mathbf{R}}\mathbf{x}\end{array}$$

代入上式即得

$${}^{\mathbf{R}}{\mathbf{u}}^T{\mathbf{F}}^{\mathbf{L}}\mathbf{u}=0$$

其中$\mathbf{F}={\mathbf{K}}_R^{-T}{\mathbf{E}\mathbf{K}}_L^{-1}$称为基本矩阵(Fundamental Matrix)，表征了同一物点在两个透视相机像素面上像素点间的几何约束关系。

本征矩阵与基本矩阵表征了两个透视模型对极几何的代数特征，以上二式共同构成对极约束(Epipolar Constraint)。

下期预告：计算机视觉系列教程15：本征矩阵、基本矩阵性质与估计