目录
整数二分
情况讨论
整数二分法因为c++是向下取整，且不存在小数分界点，因此mid有两种情况
第一种情况：
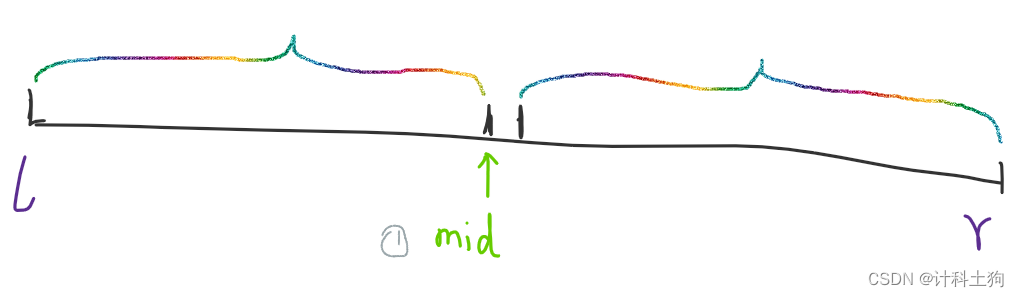
此时在进行二分法查找缩小区间时，将区间分为[l,mid]和[mid+1,r]
也就是当答案在mid的右侧时l=mid+1，当答案在mid的左侧时r=mid
此时mid=l+r>>1
第二种情况：
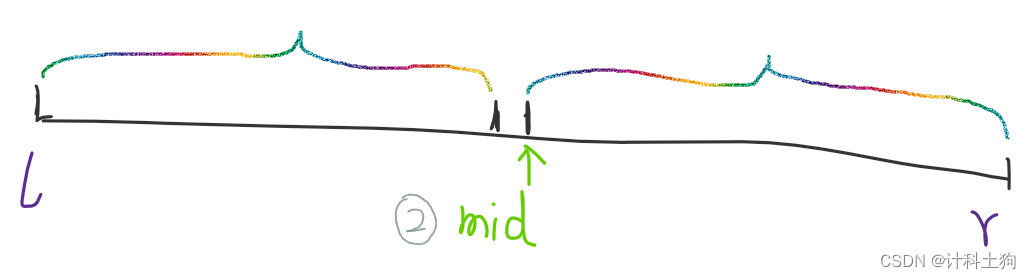此时在进行二分法查找缩小区间时，将区间分为[l,mid-1]和[mid,r]
也就是当答案在的右侧时l=mid，当答案在mid的左侧时r=mid-1
此时mid=l+r+1>>1
注意
如何快速区分是哪儿种情况我们只需要知道是l=mid还是r=mid就行
当r=mid时我们要把mid=l+r>>1
当l=mid时我们要把mid=l+r+1>>1
在这里多余的+1仅仅是为了避免二分查找时进入死循环，从而保证了二分查找的稳定性
代码实现
给定一个升序序列，对于升序序列当中的数字进行查找，序列有n个元素，进行q次查询，每次查询的元素为k，若查找到序列之中含有k则输出k出现的起始坐标和终止坐标，若未查找到则输出-1 -1
输入样例
6 3
1 2 2 3 3 4输出样例
3 4
5 5
-1 -1源代码
#include <iostream>
using namespace std;
int n,q;
const int N = 100000+10;
int a[N];
int main()
{
int n,q;
cin>>n>>q;
for(int i = 0;i < n;i ++ )cin>>a[i];
while(q--)
{
int k;
cin>>k;
int l = 0,r = n-1;
while(l<r)
{
int mid = l+r>>1;
if(a[mid]>=k)r = mid;
else l = mid + 1;
}
if(a[l]!=k)cout<<"-1 -1"<<endl;
else
{
cout<<l<<' ';
int l = 0,r = n-1;
while(l<r)
{
int mid = l+r+1>>1;
if(a[mid]<=k)l = mid;
else r = mid-1;
}
cout<<l<<endl;
}
}
return 0;
}浮点二分
情况讨论
浮点数二分没有特殊情况哦
当答案在mid右边是l=mid，当答案在mid左边时r=mid
其边界不需要考虑加一减一问题，且mid=(l+r)/2
保留几位小数1e-(2+保留小数位)
代码实现
求n的三次方根(保留四位小数)
样例输入
1000样例输出
10.0000源代码
#include <iostream>
#include <iomanip>
using namespace std;
int main()
{
double n;
cin>>n;
double l = 0,r = n;
while(r-l>1e-6)
{
double mid=(l+r)/2;
if(mid*mid*mid>=n)r=mid;
else l=mid;
}
cout<<setiosflags(ios::fixed)<<setprecision(4)<<l;
return 0;
}