AR 预测模型的 Matlab 实现
时间序列模型建模流程图
相关链接:
自协方差函数的 Matlab 实现
时间序列平稳化的 8 种方法比较及 Matlab 实现
AR 模型的预测课件
AR 模型的预测课件(附最小二乘原理)
程序源代码打包下载
开发环境
------------------------------------------------------------------------------------------------
MATLAB 版本: 9.12.0.1884302 (R2022a)
MATLAB 许可证编号: 968398
操作系统: macOS Version: 12.3 Build: 21E230
Java 版本: Java 1.8.0_202-b08 with Oracle Corporation Java HotSpot(TM) 64-Bit Server VM mixed mode
------------------------------------------------------------------------------------------------
读取数据
上证指数数据集:SH600031.csv
该数据集描述了三一重工 2017 年每日的开盘、最高、最低、收盘、成交量、成交额.
下面取连续500次成交量的观测数据进行建立时间序列模型并预测.
前 10 行数据预览
"2017/01/03" "09:35" "6.10" "6.14" "6.10" "6.13" "2851.00" "1745600.00"
"2017/01/03" "09:40" "6.13" "6.13" "6.11" "6.13" "1413.00" "865200.00"
"2017/01/03" "09:45" "6.13" "6.18" "6.12" "6.18" "5662.00" "3487800.00"
"2017/01/03" "09:50" "6.18" "6.19" "6.17" "6.18" "4891.00" "3022800.00"
"2017/01/03" "09:55" "6.17" "6.18" "6.17" "6.18" "3300.00" "2038900.00"
"2017/01/03" "10:00" "6.18" "6.18" "6.17" "6.17" "2649.00" "1635400.00"
"2017/01/03" "10:05" "6.17" "6.18" "6.16" "6.16" "3107.00" "1917000.00"
"2017/01/03" "10:10" "6.17" "6.18" "6.16" "6.18" "5671.00" "3499300.00"
"2017/01/03" "10:15" "6.18" "6.19" "6.17" "6.18" "6490.00" "4011200.00"
"2017/01/03" "10:20" "6.19" "6.19" "6.17" "6.17" "3041.00" "1877400.00"
程序源代码
clc,clear
%% 读取数据
filename='SH600031.csv';
Data = readmatrix(filename, 'OutputType', 'string');
data = str2double(Data(1:500,7));
N = length(data);
原数据可视化
程序源代码
%% 原数据可视化
figure(1)
plot(data);
title('三一重工股票成交量时序图')
ylabel('成交量')
figure(2)
histogram(data);
title('原始数列直方图')
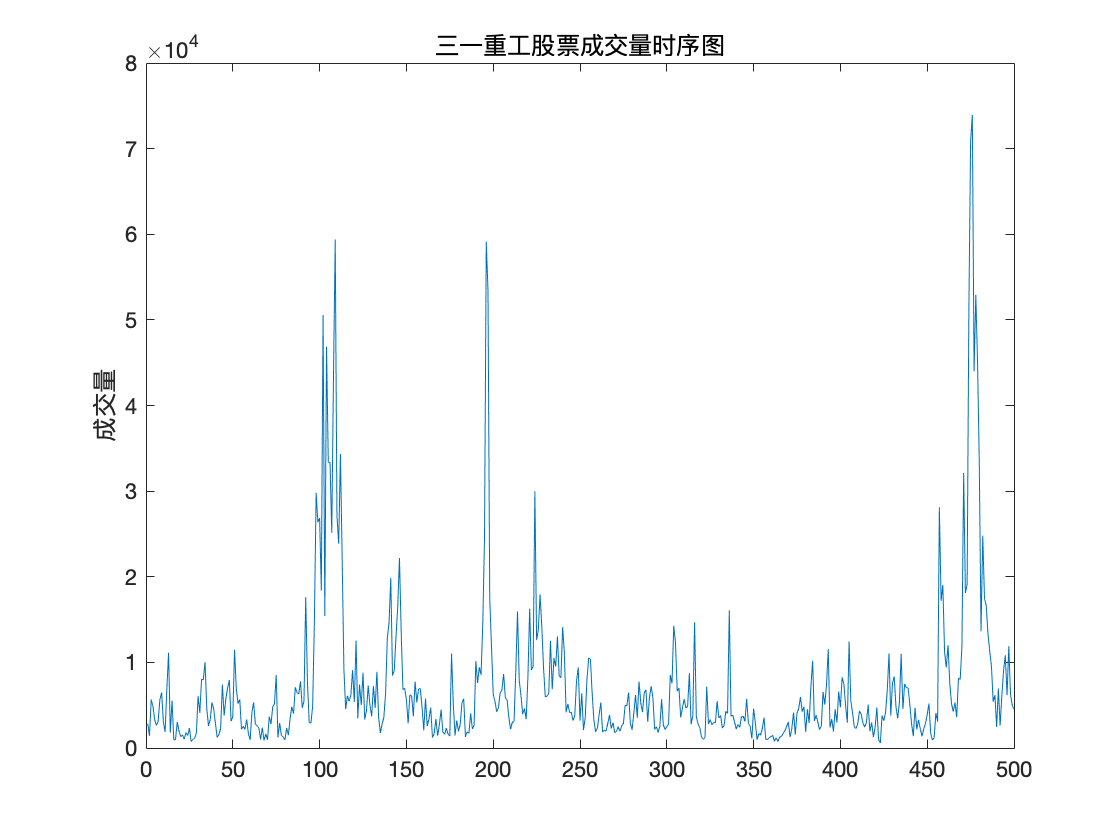
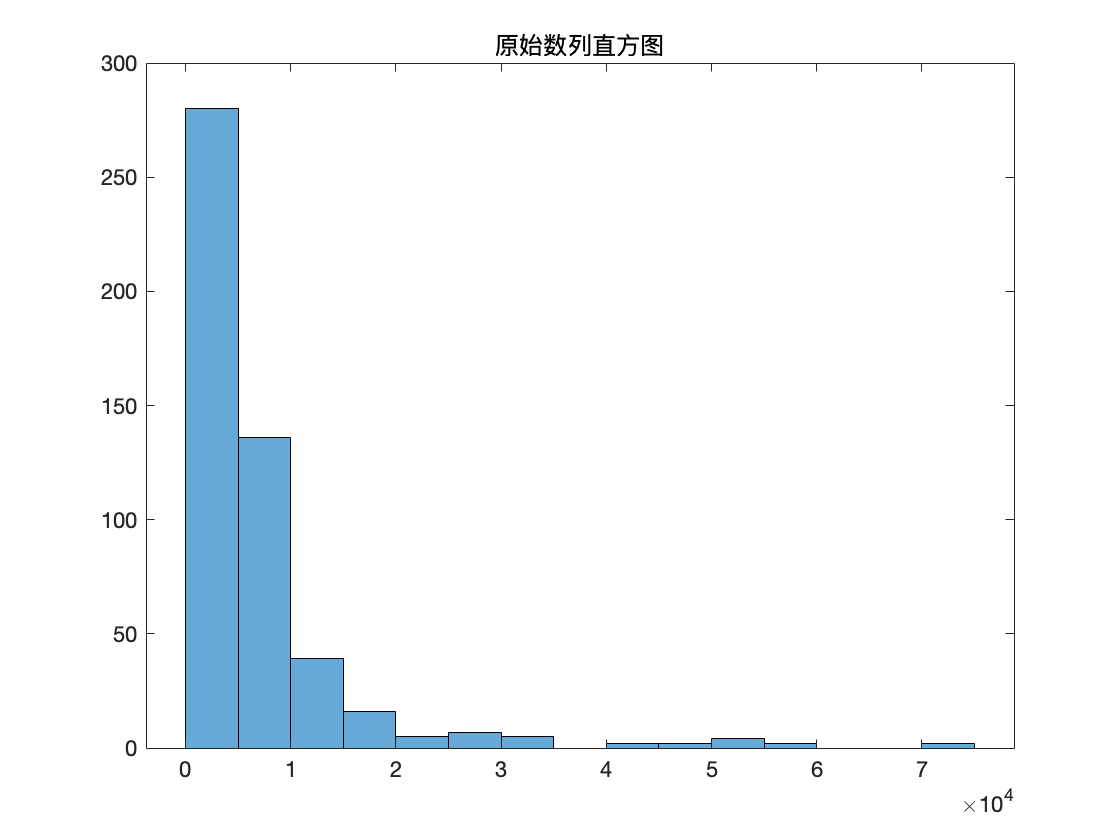
划分训练集和验证集
因为要对数据进行预测,所以我们将数据分为 70% 的训练集及 30% 的测试集.
程序源代码
%% 划分训练集和测试集
trg = round(0.7*N);
TrainData = data(1:trg);
TestData = data(trg+1:end);
数据白噪声检验
程序源代码
%% 数据白噪声检验
disp('数据白噪声检验')
[hLBQ,pLBQ] = lbqtest(TrainData);
disp('检验结果如下')
hLBQ,pLBQ
命令行窗口输出
数据白噪声检验
检验结果如下
hLBQ =
logical
1
pLBQ =
0
输出变量说明:
hLBQ 表示测试的结果
hLBQ = 1 表示拒绝数据无自相关的零假设而选择备择假设.(非白噪声序列)
hLBQ = 0 表示接受数据无自相关的零假设.(白噪声序列)
pLBQ 表示 lb 检验统计量的概率 p 值.
数据平稳性检验
程序源代码
%% 数据平稳性检验
disp('使用 PP 检验, 如果不能拒绝原假设, 则说明序列存在单位根')
[hp,hpValue,stat,cValue,reg] = pptest(TrainData,'model','Ts');
disp('检验结果如下:')
hp,hpValue
diff = 0;
while hp == 0
disp('hp=0,说明原始序列不平稳')
disp('对序列作差分处理,再对差分数据进行 PP 检验,检验结果如下:')
smooth_data = diff(TrainData);
% % 去除趋势(线性拟合)
% smooth_data=trend_fitting(smooth_data');
% % 去除趋势(多项式拟合)
% smooth_data = polynomial_fitting(smooth_data',4);
% % 去周期(季节分析)
% [smooth_data,I]= seasonal_analysis(smooth_data',12);
% % 去除趋势(k 阶差分)
% smooth_data= difference(smooth_data,1);
% % 去周期(k 步季节差分)
smooth_data= seasonal_difference(smooth_data,12);
[hp,hpValue,stat,cValue,reg] = pptest(smooth_data,'model','Ts');
hp,hpValue
diff = diff + 1;
end
disp('hp=1,原始序列平稳')
smooth_data = TrainData;
命令行窗口输出
使用 PP 检验, 如果不能拒绝原假设, 则说明序列存在单位根
检验结果如下:
hp =
logical
1
hpValue =
1.0000e-03
hp=1,原始序列平稳
模型识别
自相关及偏自相关图像
程序源代码
%% 自相关及偏自相关图像
%原序列图片
figure(3)
subplot(2,1,1)
autocorr(TrainData);
title('成交量的自相关图像')
subplot(2,1,2)
parcorr(TrainData)
title('成交量的偏自相关图像')
if diff >=1
% 平滑化后图片
figure(4)
subplot(2,1,1)
autocorr(smooth_data);
title('平稳化后的自相关图像')
subplot(2,1,2)
parcorr(smooth_data)
title('平稳化后的偏自相关图像')
end
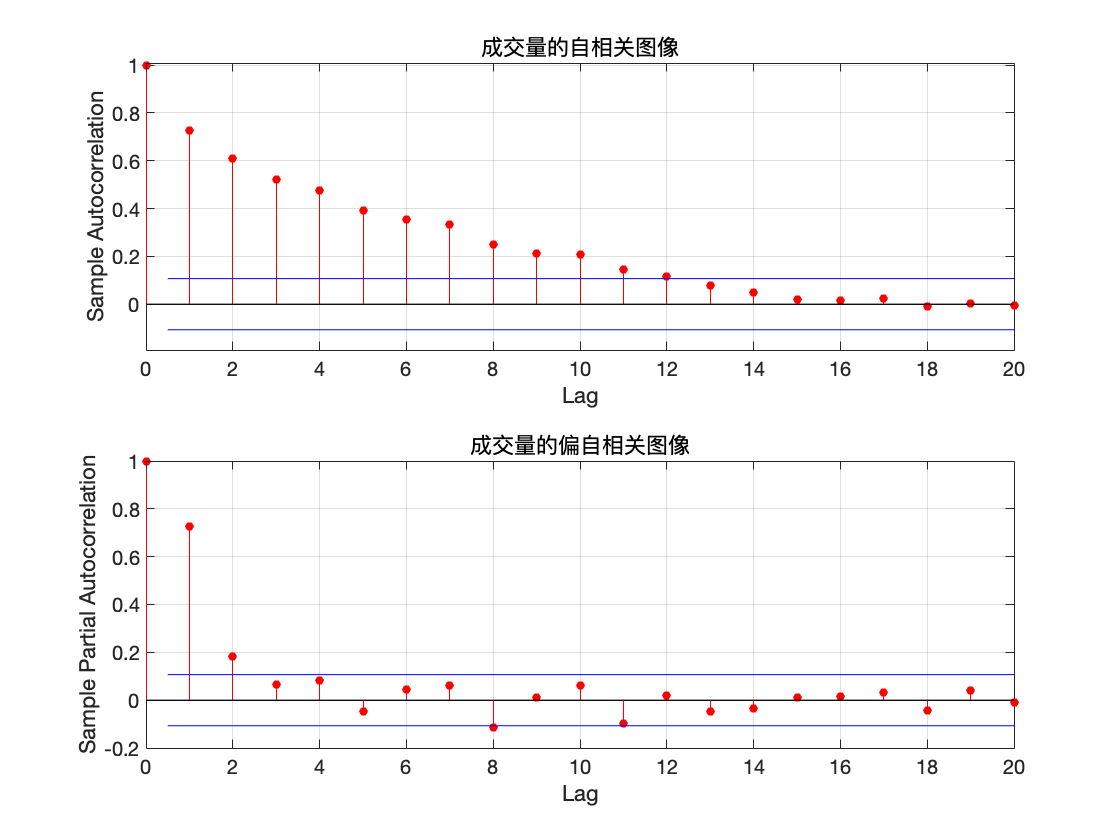
从自相关及偏自相关图像可以看出, 自相关系数缓慢衰减,可以判定自相关系数拖尾,而偏自相关系数在延迟 2 阶后都在2 倍标准差范围里面. 可以认为 2 阶后偏自相关系数为零, 所以偏自相关系数 2 阶后截尾, 由 AR 模型的统计特性,可以初步判定该数据是 AR(2) 模型.
AIC & BIC 准则定阶
在对 AR 模型识别时, 根据其样本偏自相关系数的截尾步数, 可初步得到 A R \mathrm{AR} AR 模型的阶数 p p p. 然而, 此时建立的 AR ( p ) \operatorname{AR}(p) AR(p) 模型末必是最优的. 一个好模型通常要求残差序列方差较小, 同时模型也相对简单, 即要求阶数较低. 因此, 我们需要一些准则来比较不同阶数的模型之间的优劣, 从而确定最合适的阶数.
- Akaike 信息准则
Akaike 信息准则, 简称为 AIC 准则, 是一种基于观测数据选择最优参数模型的信息准则, 它既要衡量模型对原始数据的拟合程度, 又要考虑模型中所含待估参数的个数, 即模型的复杂程度.
定义 AIC 信息准则如下:
AIC ( p ) = ln σ ^ 2 + 2 ( p + 1 ) N , \operatorname{AIC}(p)=\ln \hat{\sigma}^{2}+\frac{2(p+1)}{N}, AIC(p)=lnσ^2+N2(p+1),
其中 p + 1 p+1 p+1 为待估参数个数, 即 AR ( p ) \operatorname{AR}(p) AR(p) 模型的 p p p 个自回归系数 a 1 , ⋯ , a p a_{1}, \cdots, a_{p} a1,⋯,ap 以及随机误差的方差 σ 2 \sigma^{2} σ2.
程序源代码
%% AIC 准则定阶
maxLags = 8;
AIC = zeros(maxLags,1);
for j=1:maxLags
mdl = ar(smooth_data,j);
AIC(j) = mdl.Report.Fit.AIC;
end
% 画热度图来表示 AIC 数值的分布
figure(4)
heatmap(AIC/1000);
xlabel("AIC")
ylabel("AR Lags")
OptimalARLags_AIC = find(AIC==min(AIC));
title('Optimal AR ')
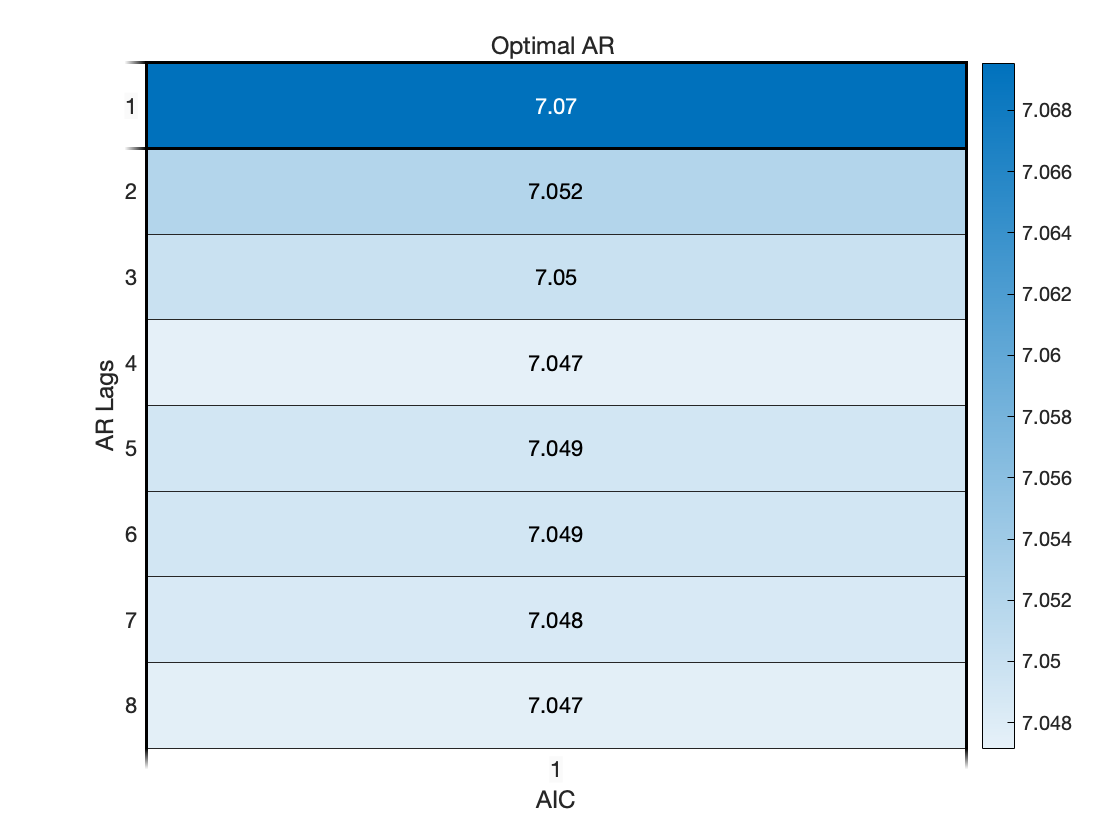
AIC 准则下的最优 AR 模型的阶数为 4 阶.
- BIC 准则
模拟研究结果表明, 当观测序列长度 N N N 较大时, AIC 准则有使 p p p 值估计 过高的倾向. 通过修正拟合残差方差和拟合模型参数个数之间的权重, 得到贝叶斯信息准则, 简称为 BIC 准则, 其定义如下:
B I C ( p ) = ln σ ^ 2 + ln N ( p + 1 ) N . \mathrm{BIC}(p)=\ln \hat{\sigma}^{2}+\frac{\ln N(p+1)}{N} . BIC(p)=lnσ^2+NlnN(p+1).
A I C \mathrm{AIC} AIC 准则与 BIC 准则的差异仅在于将 A I C \mathrm{AIC} AIC 中后一项中的 2 换为 ln N \ln N lnN, 而这一项表示模型阶数 p p p 对 AIC 和 BIC 取值大小的作用, 2 和 ln N \ln N lnN 相当于对 p p p 的加权系数. 当 N N N 较大时, 有 ln N ≫ 2 \ln N \gg 2 lnN≫2, 因此在 BIC 准则中模型阶数 p p p 的 增加对 BIC 值的影响较大, 所以 BIC 准则确定的实用模型的阶数将低于 AIC 准则确定的阶数. 可以证明, BIC 准则确定的模型阶数是其真值的一致估计.
事实上, 定义不同的准则函数, 是为了对拟合残差与参数个数之间进行不同的权衡, 以体现使用者在模型拟合误差与模型复杂程度之间的不同侧重.
程序源代码
%% BIC 准则定阶
maxLags = 8;
BIC = zeros(maxLags,1);
for j=1:maxLags
mdl = ar(smooth_data,j);
BIC(j) = mdl.Report.Fit.BIC;
end
% 画热度图来表示 BIC 数值的分布
figure(5)
heatmap(BIC/1000);
xlabel("BIC")
ylabel("AR Lags")
OptimalARLags_BIC = find(BIC==min(BIC));
title('Optimal AR ')
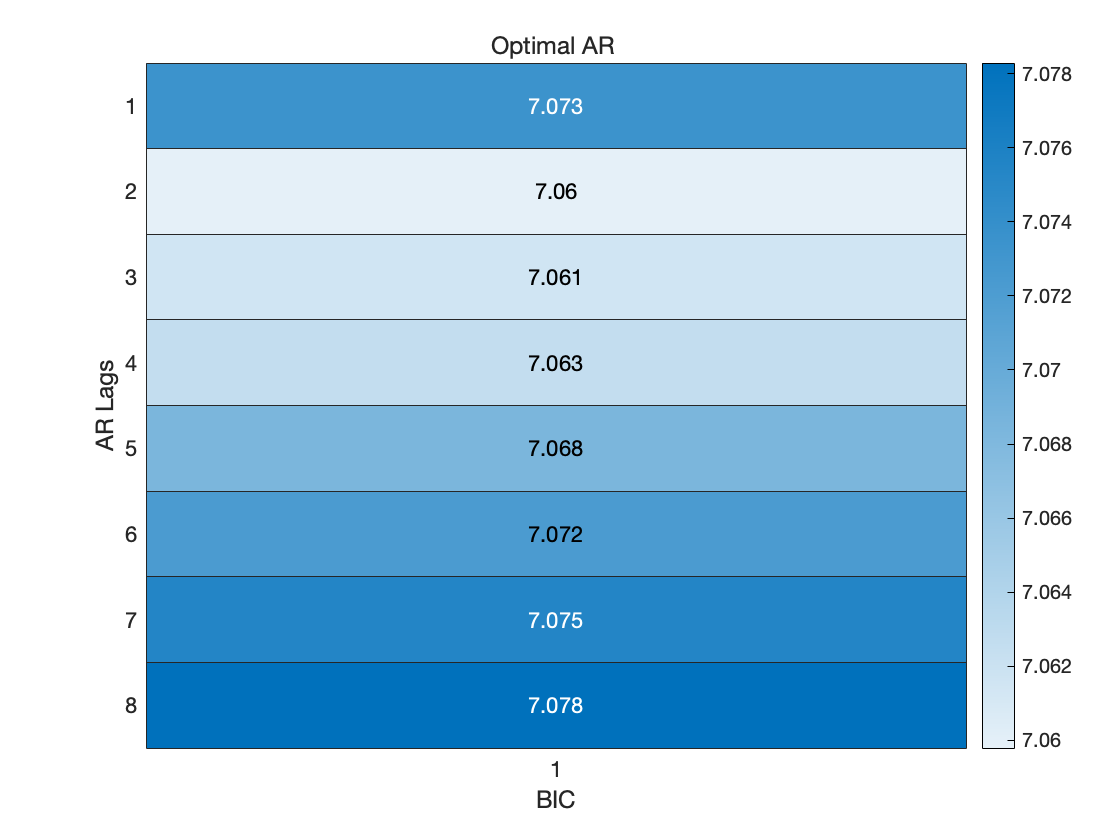
BIC 准则下的最优 AR 模型的阶数为 2 阶.
参数估计
通过以上分析可知, BIC 准则下的最优 AR 模型的阶数为 2 阶. 于是考虑建立 AR(2) 模型.
程序源代码
%% 参数估计
disp("建立的 AR 模型如下")
mdl = ar(smooth_data,OptimalARLags_BIC)
a = zeros(length(mdl.Report.Parameters.ParVector),1);
a(1:length(mdl.Report.Parameters.ParVector)) = -mdl.Report.Parameters.ParVector;
命令行窗口输出
建立的 AR 模型如下
mdl =
Discrete-time AR model: A(z)y(t) = e(t)
A(z) = 1 - 0.6436 z^-1 - 0.2325 z^-2
采样时间: 1 seconds
Parameterization:
Polynomial orders: na=2
Number of free coefficients: 2
Use "polydata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using AR ('fb/now') on time domain data "smooth_data".
Fit to estimation data: 30.82%
FPE: 3.296e+07, MSE: 3.259e+07
残差的白噪声检验
程序源代码
%% 残差的白噪声检验
epsilon = zeros(length(TrainData)-OptimalARLags_BIC,1);
x_hat = zeros(length(TrainData)-OptimalARLags_BIC,1);
for j =OptimalARLags_BIC+1:length(TrainData)
x_hat(j) = smooth_data(j-OptimalARLags_BIC:j-1)'*flipud(a(1:length(mdl.Report.Parameters.ParVector)));
epsilon(j) = smooth_data(j) - x_hat(j);
end
var_epsilon = var(epsilon);
mean_epsilon=mean(epsilon);
figure(6)
subplot(1,2,1)
qqplot((epsilon-mean_epsilon)/sqrt(var_epsilon))
x = -4:.05:4;
[f,xi] = ksdensity((epsilon-mean_epsilon)/sqrt(var_epsilon));
subplot(1,2,2)
plot(xi,f,'k','LineWidth',2);
hold on
plot(x,normpdf(x),'r--','LineWidth',2);
legend('标准化残差','标准正态')
hold off
figure(7)
subplot(2,1,1)
plot((epsilon-mean_epsilon)/sqrt(var_epsilon));
title('标准化残差的时序图')
subplot(2,1,2)
autocorr((epsilon-mean_epsilon)/sqrt(var_epsilon))
title('标准化残差的自相关图像')
disp('检查残差是否存在相关性')
[hLBQ,pLBQ] = lbqtest(epsilon);
disp('检验结果如下')
hLBQ,pLBQ
命令行窗口输出
检查残差是否存在相关性
检验结果如下
hLBQ =
logical
0
pLBQ =
0.1111
输出变量说明
hLBQ 表示测试的结果
hLBQ = 1 表示拒绝数据无自相关的零假设而选择备择假设.(非白噪声序列)
hLBQ = 0 表示接受数据无自相关的零假设.(白噪声序列)
pLBQ 表示 lb 检验统计量的概率 p 值.
可以看到此时 hLBQ = 0, 于是可判定残差不具有相关性, 因此模型可以信任.
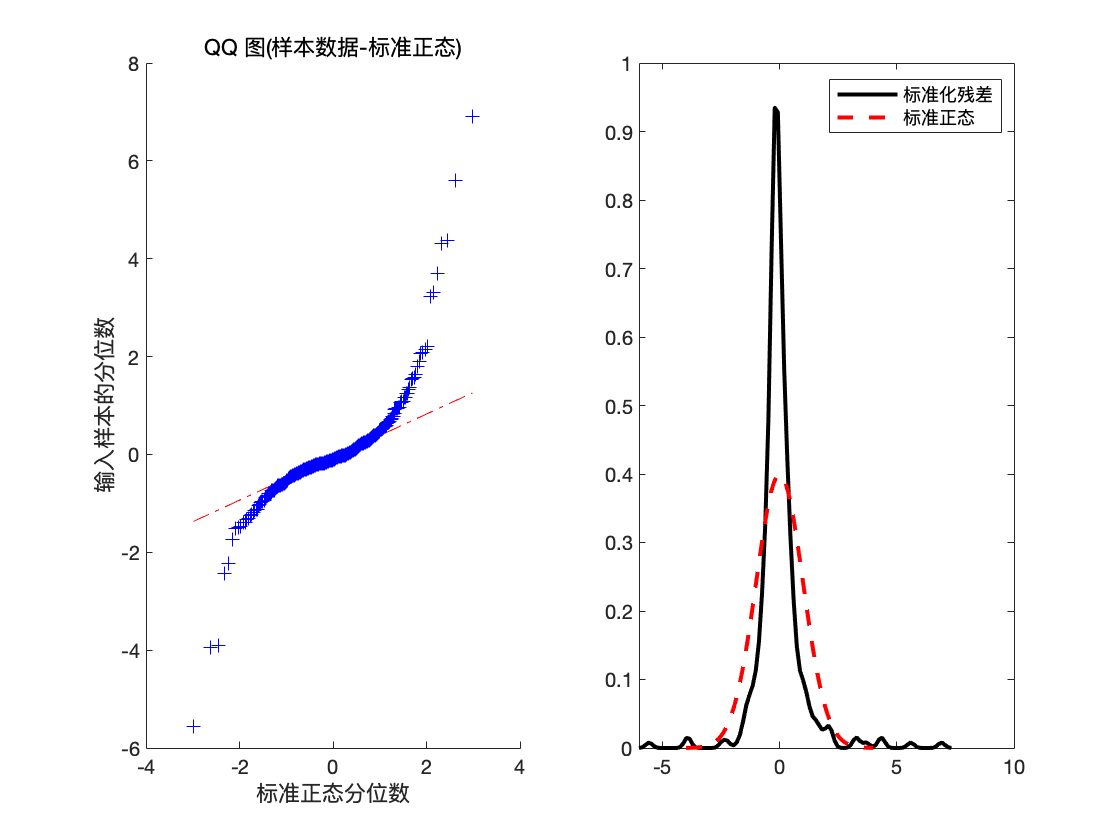
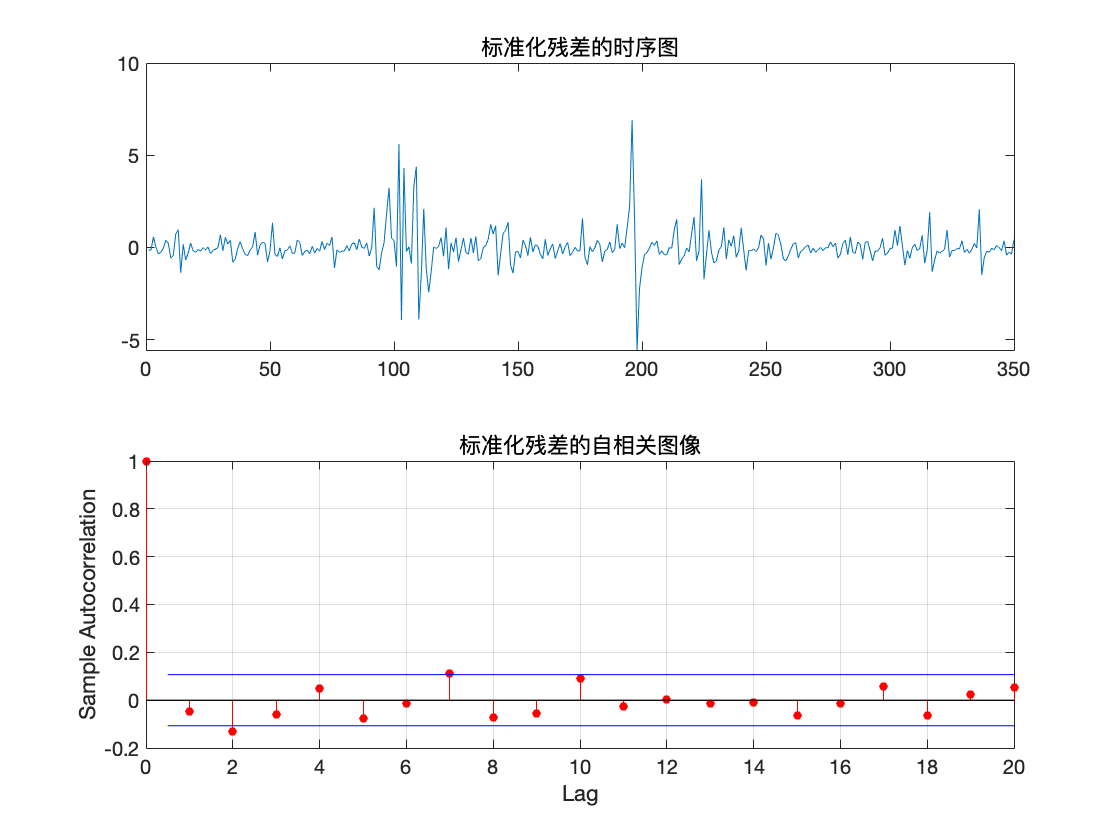
预测
我们利用建好的模型进行最佳线性预测,预测训练集后的数据,并画出预测数据的 95 % 95\% 95% 置信区间.
X t + k X_{t+k} Xt+k 的最佳线性预测可表示为
X ^ t ( k ) = L ( X t + k ∣ X t ) = { ∑ j = 1 p a j X t + 1 − j k = 1 ∑ j = 1 k − 1 a j X ^ t ( k − j ) + ∑ j = k p a j X t + k − j , 1 < k ⩽ p ∑ j = 1 p a j X ^ t ( k − j ) , k > p \begin{aligned} \hat{X}_{t}(k) &=L\left(X_{t+k} \mid \boldsymbol{X}_{t}\right) \\ &= \begin{cases}\sum_{j=1}^{p} a_{j} X_{t+1-j}& k=1 & \\ \sum_{j=1}^{k-1} a_{j} \hat{X}_{t}(k-j)+\sum_{j=k}^{p} a_{j} X_{t+k-j}, & 1<k \leqslant p \\ \sum_{j=1}^{p} a_{j} \hat{X}_{t}(k-j), & k>p\end{cases} \end{aligned} X^t(k)=L(Xt+k∣Xt)=⎩⎪⎨⎪⎧∑j=1pajXt+1−j∑j=1k−1ajX^t(k−j)+∑j=kpajXt+k−j,∑j=1pajX^t(k−j),k=11<k⩽pk>p
预测的 ( 1 − α ) (1-\alpha) (1−α) 的置信区间为
( x ^ t ( k ) ± z α 2 ( 1 + g 1 2 + ⋯ + g k − 1 2 ) 1 2 σ ) \left(\hat{x}_{t}(k) \pm z_{\frac{\alpha}{2}}\left(1+g_{1}^{2}+\cdots+g_{k-1}^{2}\right)^{\frac{1}{2}} \sigma\right) (x^t(k)±z2α(1+g12+⋯+gk−12)21σ)
式中 z α 2 z_{\frac{\alpha}{2}} z2α 表示标准正态分布的上 α 2 \frac{\alpha}{2} 2α 分位数.
程序源代码
%% 预测
step = 150;
% 计算 AR(2) 的 Green 系数
g = zeros(step,1);
g(1) = 1;
g(2) = a(1)*g(1);
for j = 3:step
g(j) = a(1)*g(j-1) + a(2)*g(j-2);
end
Yf_1 = forecast(mdl,smooth_data,step);
Yf_2 = zeros(N,1);
Yf_2(1:length(smooth_data))=smooth_data;
YMSE = zeros(N,1);
for k =length(TrainData)+1:length(TrainData)+step
Yf_2(k) = Yf_2(k-OptimalARLags_BIC:k-1)'*flipud(a(1:length(mdl.Report.Parameters.ParVector)));
YMSE(k) = sum(g(1:k-length(TrainData)).^2)*var(epsilon);
end
error = Yf_1-Yf_2(length(smooth_data)+1:end);
figure(8)
plot(error)
ylabel('差值')
max_error = max(error);
fprintf('最大模范数:%f\n',max_error);
upper = Yf_2 + 1.96*sqrt(YMSE);
lower = Yf_2 - 1.96*sqrt(YMSE);
figure(9)
h1 = plot(data,'b');
hold on
h2 = plot(trg + 1:trg + step,Yf_2(trg + 1:trg + step),'r','LineWidth',2);
h3 = plot(trg + 1:trg + step,upper(trg + 1:trg + step),'k--','LineWidth',1.5);
plot(trg + 1:trg + step,lower(trg + 1:trg + step),'k--','LineWidth',1.5);
title('预测结果(95% 置信区间)')
ylabel('成交量')
legend([h1,h2,h3],'原始数据','预测值','95% 置信区间','Location','NorthWest')
hold off
命令行窗口输出
最大模范数:0.000000
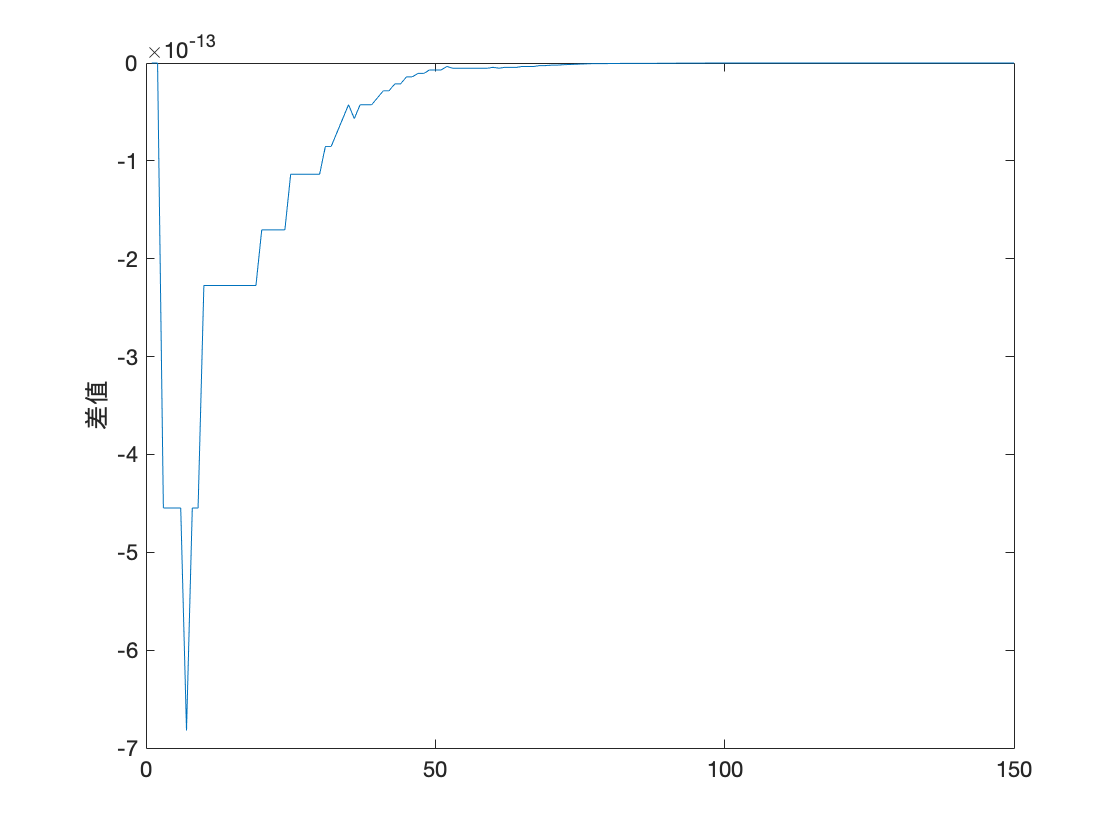
可以看到调用
Matlab自带的预测函数forecast与使用作者根据最佳线性预测公式计算的预测值残差达到 1 0 − 13 10^{-13} 10−13 量级, 由此可以验证此部分程序的正确性.
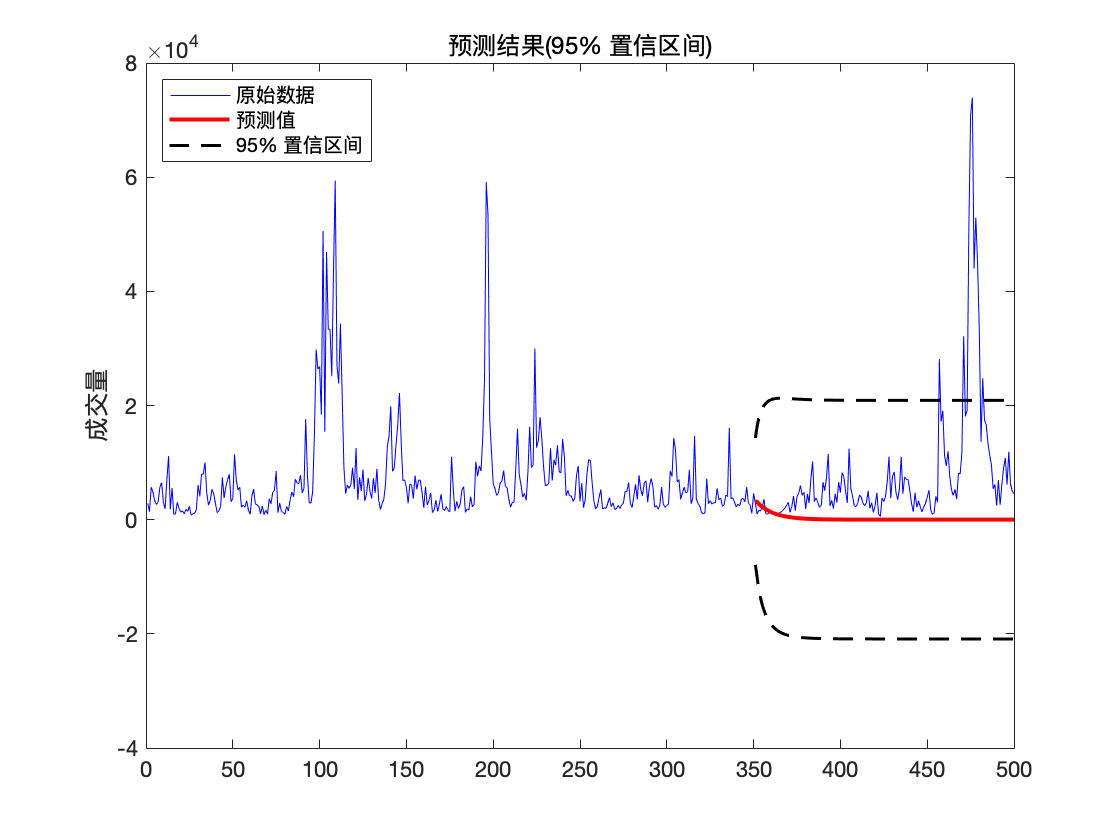
可以看到未来走势在 95 % 95\% 95% 置信区间内.
修正预测
预测的步长越长, 末知信息就越多, 从而估计的精度就越差. 然而, 随着时间的发展, 我们在原有的观测值 { ⋯ , x t − 1 , x t } \left\{\cdots, x_{t-1}, x_{t}\right\} { ⋯,xt−1,xt} 的基础上, 不断获得新的观测 值 { x t + 1 , x t + 2 , ⋯ } \left\{x_{t+1}, x_{t+2}, \cdots\right\} { xt+1,xt+2,⋯}. 这些新观测值带来更多的信息, 从而预测末来时刻的末知信息逐渐减少. 因此, 利用新观测值的信息, 我们可以更好地预测末来的序列值 x t + k x_{t+k} xt+k, 预测精度将提高. 这就是所谓的修正预测.
修正预测有两种处理方式. 一种处理方法是把新的观测值和原数据合并, 重新拟合模型, 然后再利用拟合后的模型预测 x t + k x_{t+k} xt+k; 另一种处理方法是利用原 来的拟合模型, 然后利用新观测值修正原来的拟合模型, 从而得到新的拟合模型. 当新的观测序列很多时或易于操作时, 可采用第一种方法. 然而, 当新的观 测并不多时, 第一种方法不是最佳选择. 此时, 第二种方法将更加简便. 下面介绍第二种处理方法.
一般地, 假如获得新观测值 x t + 1 , ⋯ , x t + l ( 1 ⩽ l < k ) x_{t+1}, \cdots, x_{t+l}(1 \leqslant l<k) xt+1,⋯,xt+l(1⩽l<k), 则 x t + k x_{t+k} xt+k 的修正预测值为
x ^ t + 1 ( k − 1 ) = g k − l ε t + l + ⋯ + g k − 1 ε t + 1 + g k ε t + g k + 1 ε t − 1 + ⋯ = g k − l ε t + l + ⋯ + g k − 1 ε t + 1 + x ^ t ( k ) \begin{aligned} \hat{x}_{t+1}(k-1) &=g_{k-l} \varepsilon_{t+l}+\cdots+g_{k-1} \varepsilon_{t+1}+g_{k} \varepsilon_{t}+g_{k+1} \varepsilon_{t-1}+\cdots \\ &=g_{k-l} \varepsilon_{t+l}+\cdots+g_{k-1} \varepsilon_{t+1}+\hat{x}_{t}(k) \end{aligned} x^t+1(k−1)=gk−lεt+l+⋯+gk−1εt+1+gkεt+gk+1εt−1+⋯=gk−lεt+l+⋯+gk−1εt+1+x^t(k)
其中 ε t + j = x t + j − x ^ ( t + j − 1 ) + 1 ( 1 ⩽ j ⩽ l ) \varepsilon_{t+j}=x_{t+j}-\hat{x}_{(t+j-1)+1}(1 \leqslant j \leqslant l) εt+j=xt+j−x^(t+j−1)+1(1⩽j⩽l) 为 x t + j x_{t+j} xt+j 的一步预测误差. 此时, 修正后的预测方差为
Var ( e t + l ( k − l ) ) = ( 1 + g 1 2 + ⋯ + g k − l − 1 2 ) σ 2 . \operatorname{Var}\left(e_{t+l}(k-l)\right)=\left(1+g_{1}^{2}+\cdots+g_{k-l-1}^{2}\right) \sigma^{2} . Var(et+l(k−l))=(1+g12+⋯+gk−l−12)σ2.
从上面的分析可知, 当我们获得新的观测值时, 修正后的预测方差将减少, 从而提高了预测精度. 而且这种修正方式简单, 易于操作.
程序源代码
%% 修正预测
step = 150;
% 计算 AR(2) 的 Green 系数
g = zeros(N,1);
g(N-step + 1) = 1;
g(N-step + 2) = a(1)*g(N-step + 1);
for j = N-step + 3:N
g(j) = a(1)*g(j-1) + a(2)*g(j-2);
end
% Revised_forecast = forecast(mdl,smooth_data,step);
Revised_forecast = zeros(N,1);
Revised_forecast(1:length(smooth_data))=smooth_data;
YMSE = zeros(N,1);
epsilon_hat = zeros(N,1);
for l = 1:120
for k =length(TrainData)+1:length(TrainData)+l
Revised_forecast(k) = Revised_forecast(k-OptimalARLags_BIC:k-1)'*flipud(a(1:length(mdl.Report.Parameters.ParVector)));
epsilon_hat(k) = TestData(k-length(TrainData)) - Revised_forecast(k);
end
for k =length(TrainData)+1:length(TrainData)+step
Revised_forecast(k) = Revised_forecast(k-OptimalARLags_BIC:k-1)'*flipud(a(1:length(mdl.Report.Parameters.ParVector)));
Revised_forecast(k) = Revised_forecast(k) + g(k+1-l:k+1-1)'*flipud(epsilon_hat(length(TrainData)+1:length(TrainData)+l));
YMSE(k) = sum(g(1:k).^2)*var(epsilon);
end
upper = Revised_forecast + 1.96*sqrt(YMSE);
lower = Revised_forecast - 1.96*sqrt(YMSE);
figure(10)
h1 = plot(data,'b');
hold on
h2 = plot(trg + 1:trg + step,Revised_forecast(trg + 1:trg + step),'r','LineWidth',2);
h3 = plot(trg + 1:trg + step,upper(trg + 1:trg + step),'k--','LineWidth',1.5);
plot(trg + 1:trg + step,lower(trg + 1:trg + step),'k--','LineWidth',1.5);
title(['获得 ',num2str(l),' 个新观测值后修正预测结果(95% 置信区间)'])
ylabel('成交量')
legend([h1,h2,h3],'原始数据','预测值','95% 置信区间','Location','NorthWest')
hold off
getframe;
end
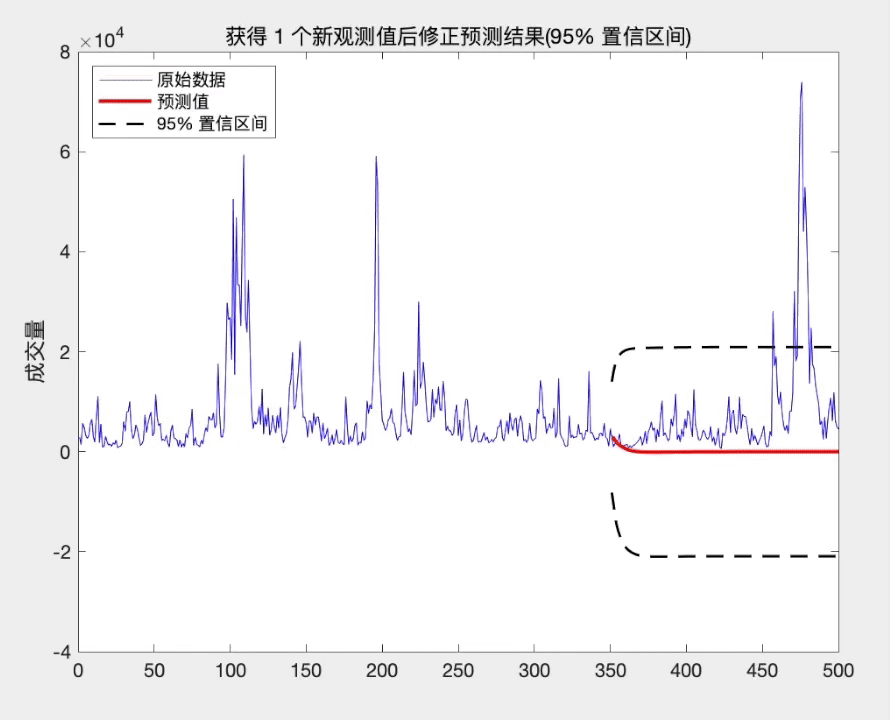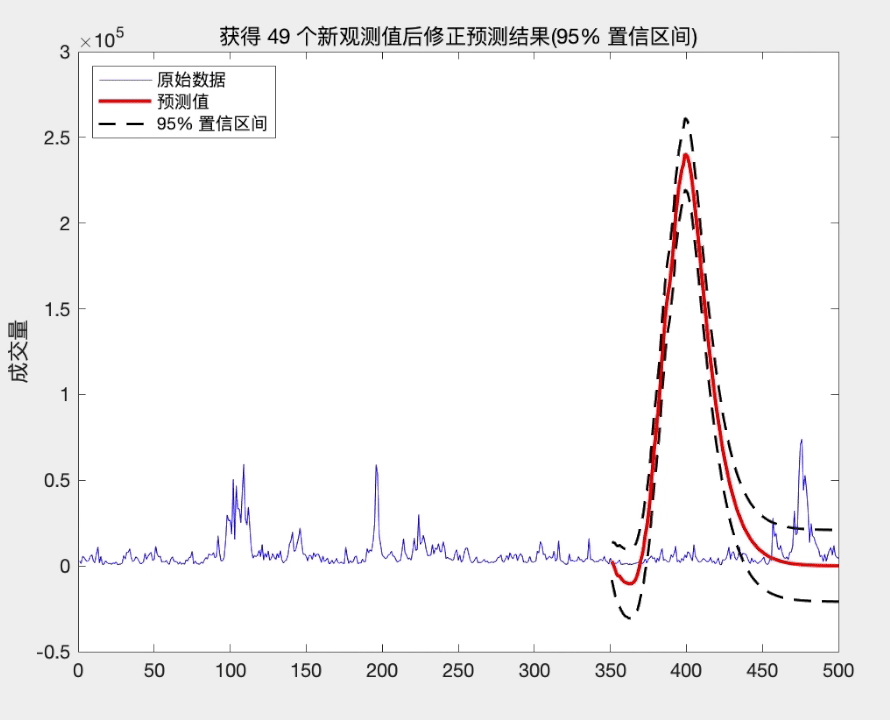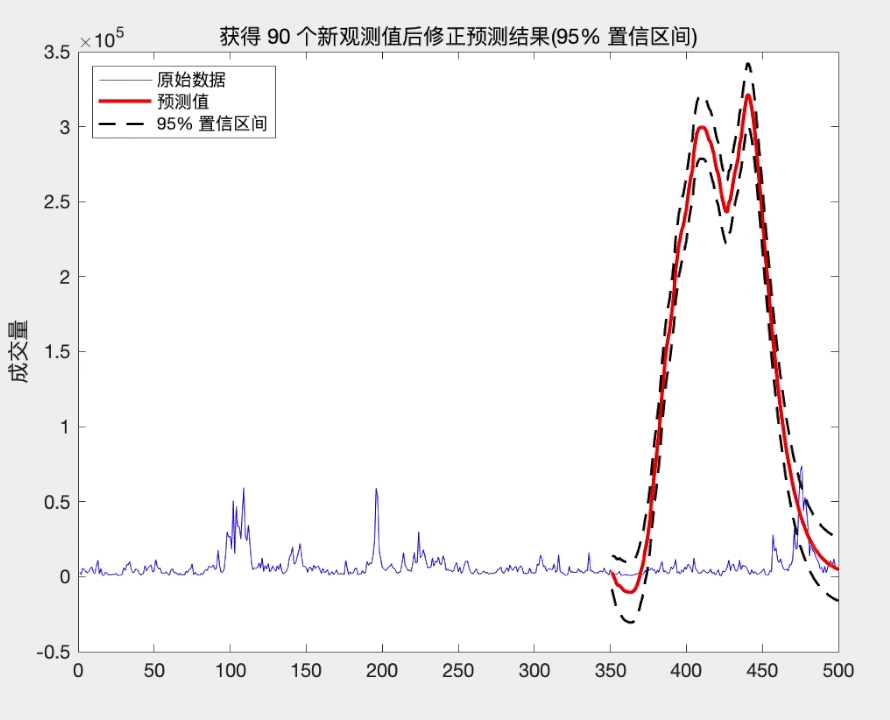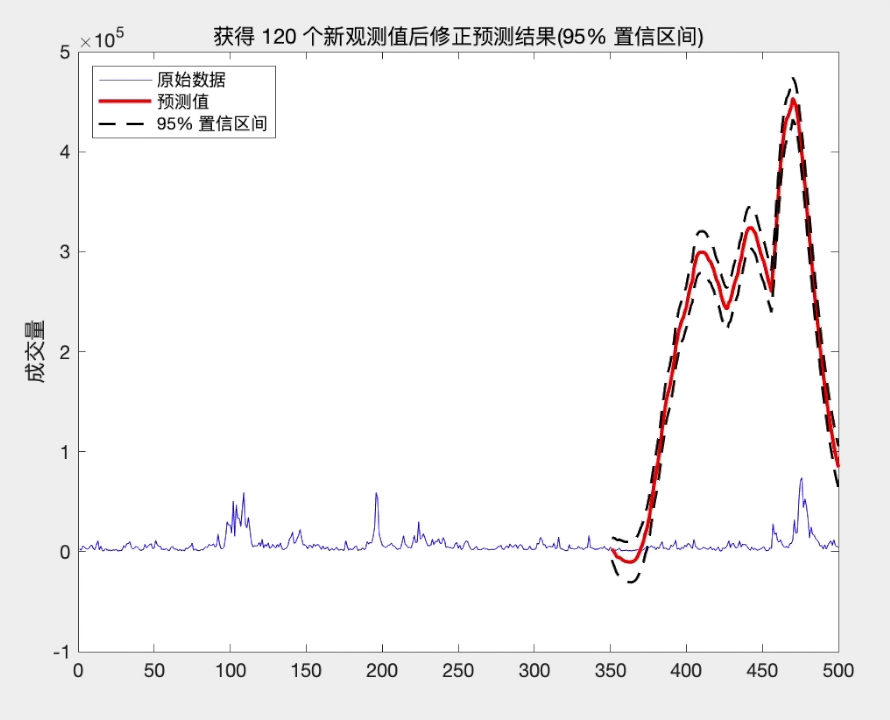
参考文献
[1] 周永道,王会琦,吕王勇. 时间序列分析及应用. 北京:高等教育出版社,2015.
[2] 江渝,李幸,卓金武. MATLAB时间序列方法与实践. 北京:电子工业出版社,2019.
[3] 茆诗松,程依明,濮晓龙. 概率论与数理统计教程. 北京:高等教育出版社,2011.
本人非统计专业,若有不妥之处, 恳请批评指正.
作者: 图灵的猫
作者邮箱: [email protected]