1.实现一个计数器
class Calculator{
private int num1;
private int num2;
public int getNum1() {
return num1;
}
public void setNum1(int num1) {
this.num1 = num1;
}
public int getNum2() {
return num2;
}
public void setNum2(int num2) {
this.num2 = num2;
}
public int add()
{
return num1+num2;
}
public int sub()
{
return num1-num2;
}
public double mul()
{
return num1*num2;
}
public double dev()
{
return num1/num2;
}
}
public class test {
public static void main(String[] args) {
Calculator calculator=new Calculator();
calculator.setNum1(10);
calculator.setNum2(5);
System.out.println(calculator.add());
System.out.println(calculator.sub());
}
}
2.交换两个数的值
public static void swap(Integer s1,Integer s2)
{
int temp=s1.num;
s1.num=s2.num;
s2.num=temp;
}
public static void main(String[] args) {
Integer s1=new Integer();
s1.num=10;
Integer s2=new Integer();
s2.num=20;
swap(s1,s2);
System.out.println(s1.num);
System.out.println(s2.num);
}3.时间复杂度与空间复杂度
时间复杂度是衡量一个算法的运行速度,空间复杂度是衡量一个算法所需要的额外空间
算法中基本操作的执行次数称之为算法的时间复杂度
我们再进行计算时间复杂度的时候
1)用常数1取代运行时间的所有加法常数
2)在修改后的运行次数函数中,只保留最高阶项
3)如果在高阶项存在况且不是1,那么就去除与这个项相乘的常数,得到的结果就是O阶
例1:
注意:我们根据第三条来说,如果算出的时间复杂度是3N^2;那么最终的时间复杂度就是N^2
void func1(int N){
int count = 0;
for (int i = 0; i < N ; i++) {
for (int j = 0; j < N ; j++){
count++;
}
}
for (int k = 0; k < 2 * N ; k++)
{
count++;
}
int M = 10;
while ((M--) > 0)
{count++;}
System.out.println(count);
}
他的时间复杂度为N^2+2N+10
只保留最高阶项,那么就把2N去掉,常数全部变成1,那么最终只剩下N^2+1;最终也就是N^2// 计算func3的时间复杂度
void func3(int N, int M)
{int count = 0;
for (int k = 0; k < M; k++)
{count++;
}
for (int k = 0; k < N ; k++)
{count++;
}
System.out.println(count);
}
O(M+N)
//计算他的时间复杂度
for (int k = 0; k < 2 * N ; k++)
{count++;}
int M = 10;
while ((M--) > 0)
{count++;}
2N+10--->O(N)
// for(int i=0;i<1000;i++)
count++;
所有常数均变成1000,那么时间复杂度就是O(1)
冒泡排序:
O(N^2)
优化O(N^2)
二分查找:log2N;
//求阶乘的时间复杂度
// 计算阶乘递归factorial的时间复杂度?
long factorial(int N) {
return N < 2 ? N : factorial(N-1) * N;
}
O(N)
//求斐波那契数列的时间复杂度
int fibonacci(int N) {
return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);
}
2^N空间复杂度:找额外的数据空间
// 计算斐波那契递归fibonacci的时间复杂度?
int fibonacci(int N) {
return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);
}
O(N)
// 计算阶乘递归factorial的时间复杂度?
long factorial(int N) {
return N < 2 ? N : factorial(N-1) * N;
}
O(N)
//冒泡排序的时间复杂度是O(1)
1.顺序表----将数组写到类里面,就可以面向对象了,实现了很多功能;
1)我现在new 了一个数组,长度是10,我现在要放以下元素22,33,44,55,66,77,现在我开始进行存放
2)我放了22,33,44之后我想要知道数组的有效元素的个数怎么办?
有的人可能会想,我放了22,33,44之后,后面的元素不都默认是0了吗?我现在进行遍历数组,使用一个count变量,来进行++,遇到0就进行返回,但是如果我此时放的元素是0,22,33,44,那么此时与遍历返回的count变量是0,那么这显然是不正确的;所以数组中的元素恰好是0就不行,所以一个单独的数组是不可以进行有效数据的;
3)我已我们需要有一个数据来进行记录数组的个数;
他是一段物理地址连续的存储单元依次储存数据元素的线性结构,一般情况下采用数组进行储存,他主要是适用于确定知道要存多少数据的场景,否则开辟的空间大了浪费,开辟的空间小了还不够用
1.在进行新增元素的时候,要考虑数组长度满了(usedsize==arr1.length)的时候如何进行扩容(Arrays.copyOf),新增元素的数组下标是否合法(pos<0||pos>usedsize)
int i=usedsize-1;i>=pos;i--;---->arr1[i+1]=arr1[i]------->arr1[pos]=data;所以我们在新进行挪元素的时候,一定要从数组的最后一个位置开始挪;
class MyarrayList{
public int[] arr1;
public int usedsize;
MyarrayList(){
//初始化的时候给数组一个长度
this.arr1=new int[10];//此处的arr1这个引用在堆上面,new int[10]也是在堆上
usedsize=0;//表式当前的有效的数据个数
}
public void display()//打印数组的每一个元素
{
for(int i=0;i<usedsize;i++)
{
System.out.println(arr1[i]+"");
}
}
public int getUsedsize()//获取到数组的长度
{
return usedsize;
}
//在pos位置添加一个元素
public boolean isFull()
{
return arr1.length==usedsize;
}
public void put(int pos,int data)
{
//1.顺序表在这里面插入元素的时候,插入元素的位置的前面一定要有元素,一定是有前驱的
//2.也要考虑到顺序表放满的条件
if(pos<0||pos>usedsize)
{
System.out.println("pos的位置是不合法的");
return;
}
if(isFull())
{
this.arr1=Arrays.copyOf(this.arr1,2*this.arr1.length);
}
for(int i=this.usedsize-1;i>=pos;i--)//从数组的最后一个位置往后挪,直到要放新数据的那个下标
{
this.arr1[i+1]=arr1[i];
}
arr1[pos]=data;
usedsize++;
}
}
MyarrayList myarrayList=new MyarrayList();
myarrayList.put(0,7);
myarrayList.put(1,1);
myarrayList.put(2,3);
myarrayList.put(3,7);
myarrayList.put(4,5);
myarrayList.put(0,90);
myarrayList.display();
放元素的时候要从0下标开始放2)获取到指定位置的元素,首先注意这里面也要判断数组下标的位置是否合法,我们在进行插入元素的时候,一定要保证有效元素的后一位之前,例如现在数组中有1,2,3,4;我们可以在0,1,2,3位置进行插入元素;我们也可以在4号位置插入元素;其次我们还要保证判断数组是否为空
public int GetPos(int pos)//获取到当前下标的元素
{
if(pos<0||pos>=usedsize)
{
System.out.println("pos位置是不合法的");
return -1;
}
if(usedsize==0)
{
System.out.println("当前数组的长度是0");
return -1;
}
return this.arr1[pos];
}
//更新当前下标的元素
public void update(int pos,int value)
{
if(pos<0||pos>=usedsize)
{
System.out.println("pos的位置是不合法的");
return;
}
if(usedsize==0)
{
System.out.println("顺序表里面没有元素");
return;
}
this.arr1[pos]=value;
}3)删除操作,我们在进行删除元素的时候,要考虑到以下几个点;
1)你所要删除的元素的顺序表是不是空的
2)查找你要删除的数字的下标
3)arr1[i]=arr1[i+1];条件i<usedsize-1;
public void remove(int data)
{
if(usedsize==0)
{
System.out.println("数组里面没有数据是不可以进行删除的");
return;
}
int index=search(data);
if(index==-1)
{
System.out.println("当下的数据在顺序表中是不存在的");
return;
}
//程序能走到这里,说明已经找到了要删除的数字,即将进行删除
for(int i=index;i<usedsize-1;i++)
{
arr1[i]=arr1[i+1];//这里面的i的值不可以写成index,arr1[index]=arr1[index+1]
}
//arr1[usesize]=null;
usedsize--;
}
public void clear()
{
usedsize=0;
//for(int i=0;i<usedsize;i++)
// {
// arr1[usedsize]=null;
// }
}2.链表(重点)
1)在顺序表中,我们不光引入了一段连续的内存,还引入了一块连续的内存空间,叫做usedsize,来表示对应数组中元素的个数,在我们增加和删除元素的时候,都会涉及到一定范围内下标的移动;
2)在我进行扩容的时候,例如说我原来想要进行扩容,以数组的二倍形式来进行扩容,但是我进行而被扩容之后只放了一个元素,扩容的效率就会大大降低,我们想要一种数据结构,再进行插入元素和删除元素的时候,都不要涉及到原来元素的插入和删除;
下面我们主要介绍的是单向,不带头非循环的和双向,不带头,非循环的链表
带头:也是有一个head(是一个傀儡节点),head里面的数据是任意的,真正的有效数据放到head.next的下一个节点之后;
循环:尾巴节点的next域指向head节点,如果next指向了head.next或者其他节点,就是带有环的链表
双向:每一个节点即存放下一个结点的地址,也保存前一个结点地址
节点:有数据域(主要是进行存放数据)和指针域(存放下一个结点的地址),本质上是一个类;
下面我们来实现一个链表:
1)用一个类来进行描述一个节点,因为链表就是一个一个的节点构成的
2)实现一个链表的类
class Node{
int data;
Node next;
public Node(int data)
{
this.data=data;
}
//经过构造方法之后,就产生了一个新的节点
}
class LinkedList {
//head和tail是每一个链表都有的属性
public Node head = null;
public Node tail = null;
public void display() {
if (head == null) {
System.out.println("此时链表中没有元素,此时是不可以进行打印的");
return;
}
Node current = head;
while (current != null)//这里不可以写成head.next!=null,否则就会少打印一个节点
{
System.out.println(current.data);
current = current.next;
}
}
public Node research(int data) {
if (head == null) {
System.out.println("此时链表中是没有元素的,是不可以进行打印的");
return null;
}
Node current = this.head;
while (current != null) {
if (current.data == data) {
return current;
}
current = current.next;
}
return null;
}
public int size() {
int count = 0;
Node current = head;
while (current != null) {
count++;
current = current.next;
}
return count;
}
public void addFirst(int data) {
//根据传过来的数据新创建一个节点,即将插入到链表里面,绑定位置的时候,一定先要搞后面
Node node = new Node(data);
//所谓的头插法就是让每一次进行新插入的元素形成的节点成为新的头节点
if (head == null) {
head = node;
tail = node;
} else {
node.next = head;
head = node;
}
}
public void addLast(int data) {
//每一次都插到链表的末尾
Node node = new Node(data);
if (head == null) {
head = node;
tail = node;
} else {
tail.next = node;
tail = tail.next;
}
}
public void addIndex(int pos, int data)
//进行插入到某一个位置,例如我们现在想要往二号位置进行插入元素
// 我们就要先进行想办法先找到一号位置的下标和对应的节点
{
//我们可以先进行定义一个节点,先走index-1步,找到前一个前驱节点,然后再进行插入
//此时我们还要进行考虑插入下标元素的位置是否是合法的,还有如果index的值是0,那么此时进行的就是头插法,如果此时index恰好等于链表的长度,此时进行的就是尾插法
if (pos < 0 || pos > size()) {
System.out.println("你进行输入的插入位置不合法");
return;
}
if (pos == 0) {
addFirst(data);
return;
} else if (pos == size()) {
addLast(data);
return;
} else {
Node front = head;
Node node = new Node(data);
while (pos - 1 != 0) {
front = front.next;
}
node.next = front.next;
front.next = node;
}
}
//删除第一次出现关键字为Key的节点
public void remove(int Key)
{
//如果我们想要删除一个链表中第一次出现的数字,就要知道这个数所在的节点A,和这个节点的前一个结点,那么我们就可以通过front.next.data=key就可以找到前一个结点了,那么我们此时一定要注意,front是不可以走到链表的最后一个节点了,如果走到了最后一个节点,那么此时就一定会出现空指针异常
//也就是说front.next.next==null,那么这个关键字在链表中是不存在的
//针对我们的头节点我们要进行特殊处理
if(head==null)
{
head=head.next;
return;
}
Node front=head;
Node cur=research(Key);
while(front.next.data!=Key&&front.next.next!=null)
{
front=front.next;
}
front.next=cur.next;
}
//删除所有出现关键字为Key的节点
public void removeAll(int key)
{
//current代表我们要进行删除的节点
//front代表我们要进行删除结点的前一个结点
Node current=head;
Node front=null;
while(current!=null)
{
if(head.data==key)
{
head=head.next;
current=head;
}else if(current.data==key){
front.next=current.next;
current=current.next;
}else{
front=current;
current=current.next;
}
}
}
public void clear()
{
head=null;
while(this.head!=null)
{
Node curNext=head.next;
head.next=null;
head=curNext;
}
}
}
class TestEnum{
public static void main(String[] args) {
LinkedList list=new LinkedList();
list.addLast(1);
list.addLast(1);
list.addLast(1);
list.addLast(4);
list.addLast(1);
list.removeAll(1);
list.display();
}
}
2.单链表常见的OJ题
1)进行反转单链表
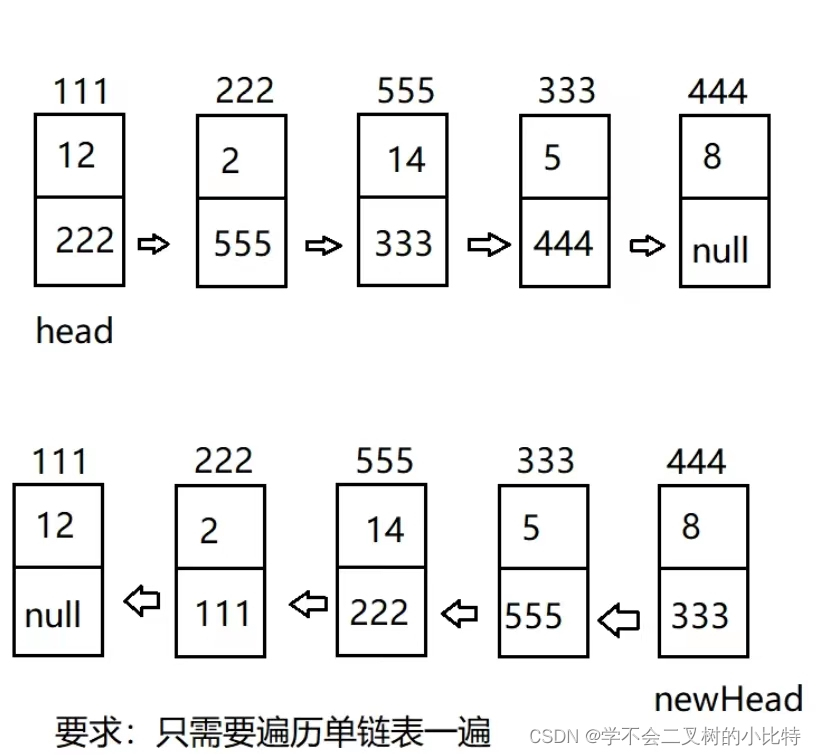
输入:1,2,3,4,5;
输出:5,4,3,2,1;
1)我们先写两个变量,front=head,current=front.next;我们设想一下只用这两个变量是否可以进行反转单链表的操作呢;
我让current.next=front,再让front=current;这是我们就发现current已经无法走到下一个节点了,因为此时current.next已经被修改了,所以我们可以让curNext来进行保存每一次反转操作的current.next的值(这个操作再循环中的第一条语句)
2)循环条件为current.next!=null;
public Node resverse()
{
if(head==null)
{
throw new RuntimeException("链表长度为空");
}
Node front=null;
Node current=head;
Node currentNext=head.next;
while(current!=null)
{ currentNext=current.next;
current.next=front;
front=current;
current=currentNext;
}
return front;
}
2.只遍历单链表一遍,找出链表的中间节点
输入:1,2,3,4,5; 返回:3
输入:1,2,3,4,5,6;返回:4;如果一个链表有两个中间节点,那么我们返回第二个节点
思路:进行快慢指针,我们可以定义一个快慢指针,一开始让fast节点和slow节点都指向head,然后我们指向循环,让fast一次走两步,让slow一次走一步;
最终slow就是中间节点
我们可以自己画图演示一下,链表长度为奇数或者链表长度是偶数的截至条件是不一样的
public ListNode middleNode(ListNode head) {
ListNode fast=head;
ListNode slow=head;
while(fast!=null&&fast.next!=null)
{
fast=fast.next.next;
slow=slow.next;
}
return slow;
3.找出链表中的倒数第K个节点,能不能遍历单链表一遍
要找到倒数第K个,要从前向后走len-k步(至少要遍历两遍,因为首先要知道链表的长度);
思路:我们进行定义两个快慢指针,fast为快指针,slow是慢指针,我们先让fast走k-1步,然后再让fast和slow同时走;等到fast.next为空的时候,并返回slow节点,这时的slow才为倒数第K个节点;
public Node returnLastK(int index)
{
if(index<0)
{
throw new UnsupportedOperationException("此时的链表的倒数第K个节点位置不正确");
}
if(head==null)
{
throw new UnsupportedOperationException("此时链表长度是空");
}
Node fast=head;
Node slow=head;
for(int i=0;i<index-1;i++)
{ fast=fast.next;
if(fast==null)
{
throw new UnsupportedOperationException("当前你输入的index的值已经超过了链表的长度");
}
}
while(fast.next!=null)
{
fast=fast.next;
slow=slow.next;
}
return slow;
}
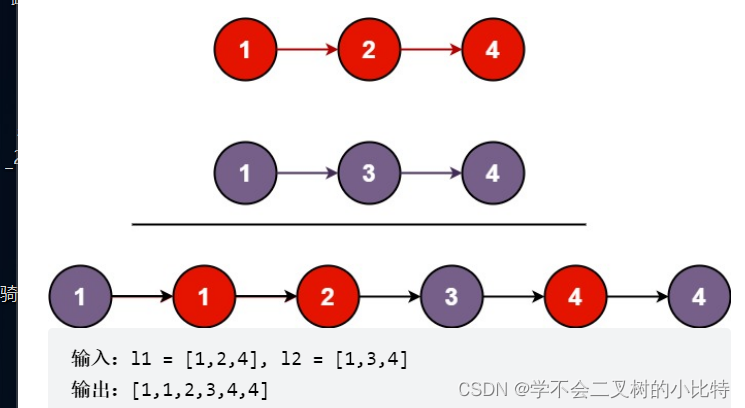
4.合并两个有序链表
思路:
1)我们首先定义一个虚拟节点是newHead作为要合并在一起的总链表的新节点,注意它是一个虚拟节点,里面的值是任意的
2)我们再合并headA和headB这两个链表的时候,保存两个链表的右节点是没有什么用处的,如果发现headA.data>headB.data,我们就把HeadA指向的这个头结点放到先开辟的链表后面,同时让headA进行向后移动
if(headA.data>headB.data)
{
}else if(HeadA.data<HeadB.data){
}else{
}
3)再进行合并的过程中,两个链表所走的过程中都不可以是空的,所以循环条件是HeadA!=null&&HeadB!=null
4)在循环出来之后,会出现一种情况,HeadA过长或者HeadB过长,此时我们还要进行特殊处理
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
ListNode HeadA=list1;
ListNode HeadB=list2;
ListNode newHead=new ListNode(-1);
ListNode temp=newHead;
while(HeadA!=null&&HeadB!=null)
{
if(HeadA.val<HeadB.val)
{
temp.next=HeadA;
HeadA=HeadA.next;
temp=temp.next;
}else
{
temp.next=HeadB;
HeadB=HeadB.next;
temp=temp.next;
}
}
if(HeadA!=null)
{
temp.next=HeadA;
}
if(HeadB!=null)
{
temp.next=HeadB;
}
return newHead.next;