目录
一.买股票的最佳时机I
1.对应letecode链接:
2.题目描述:
3.解题思路:
1.由于题目限制了我们只能进行一次股票交易。那么我们可以这样搞,我们尝试每个位置都卖出股票能获得的利润。那么最大值一定就在其中
2.假设我们在第 i天卖出股票,要想使得获利最大,那么我们一定会贪心地考虑在第 i 天之前的最低价时入手该股票。因此我们需要定义一个变量prev记录i位置之前的最小值是多少。然后按照上述流程尝试每个位置卖出能获得的利润
这时候不管股价是多少,我的收益都是0,为什么呢?因为必须要先买后卖,只有一天的情况下无法卖出,所以卖出的收益是0。
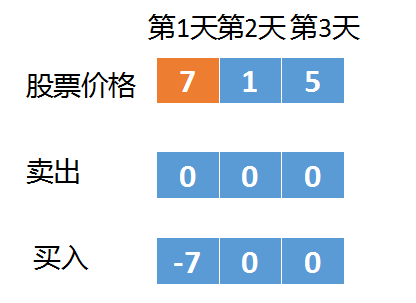
我们再来看一个复杂点的,假设有三天这里卖出数组记录了每次卖出的最大收益,数组下标i即对应第i天的最大收益买入数组记录了每次买入的最大收益,数组下标i即对应第i天的最大收益第一天的时候还是老样子,卖出是0,买入是-7。
三天卖出的利润就变了卖出收益是:第二天买入的值-1,加上第三天的股票价格,也就是前一天买入的最大收益 -1加上第三天的股票价格5,于是第三天买入的收益就变成了4买入的收益是:第二天买入的值-1vs第三天买入的股价-5,选择不动。
4.对应代码
class Solution { public: int maxProfit(vector<int>& prices) { int prevVal=prices[0];//[0....i-1]范围内的最小值 int maxRet=0; int N=prices.size(); for(int i=1;i<N;i++){ maxRet=max(maxRet,prices[i]-prevVal);//尝试以每个位置卖出能获得的利润 prevVal=min(prevVal,prices[i]); } return maxRet; } };
二.买股票的最佳时机II
1.对应letecode链接:
2.题目描述
3.解题思路:
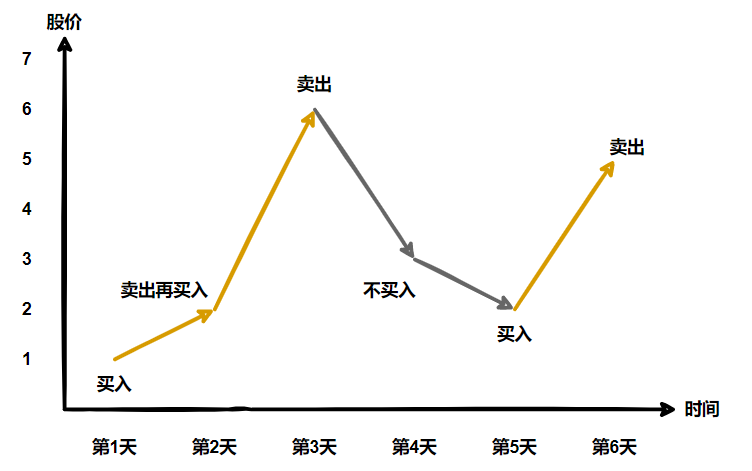
本题和上题不同的是可以交易无数次。下面我们来看一个例子:
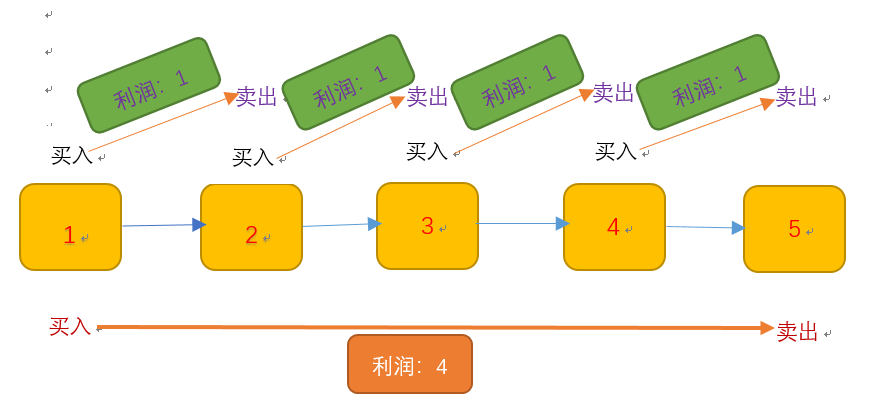
由于我们可以交易无数次,那是不是我们只要将波峰-波谷的值全部累加起来就是最大利润了。下坡的我们不要因为那是亏本的
而波峰减波谷我们也可以这样算如果后面一个位置的值减前面一个位置的值大于0那么我们就将其累加上,小于0就累加0就相当于不要它。
4.对应代码
class Solution { public: int maxProfit(vector<int>& prices) { int ans=0; for(int i=1;i<prices.size();i++){ //计算波峰-波谷的值分解成后一个减前一个是否大于0 ans+=prices[i]-prices[i-1]>0?prices[i]-prices[i-1]:0; } return ans; } };
三.买股票的最佳时机III
1.对应letecode链接:
2.题目描述:
3.解题思路:
这题其实就是股票问题四的特例具体请看股票问题四。在这里给出代码
class Solution { public: int maxProfit(vector<int>& nums) { if (nums.size() < 2) { return 0; } int N = nums.size(); vector<vector<int>>dp(N, vector<int>(2 + 1)); for (int j = 1; j <= 2; j++) { int p1 = dp[0][j]; int best = max(dp[1][j - 1] - nums[1], dp[0][j - 1] - nums[0]); dp[1][j] = max(best + nums[1], p1); for (int i = 2; i < N; i++) { int curA = dp[i - 1][j]; int a = dp[i][j - 1] - nums[i]; best = max(best, a); dp[i][j] = max(curA, best + nums[i]); } } return dp[N - 1][2]; } //prices从[0.....index]范围内任意交换能获得的最大利润 };
四.股票问题IV
1.对应letecode链接
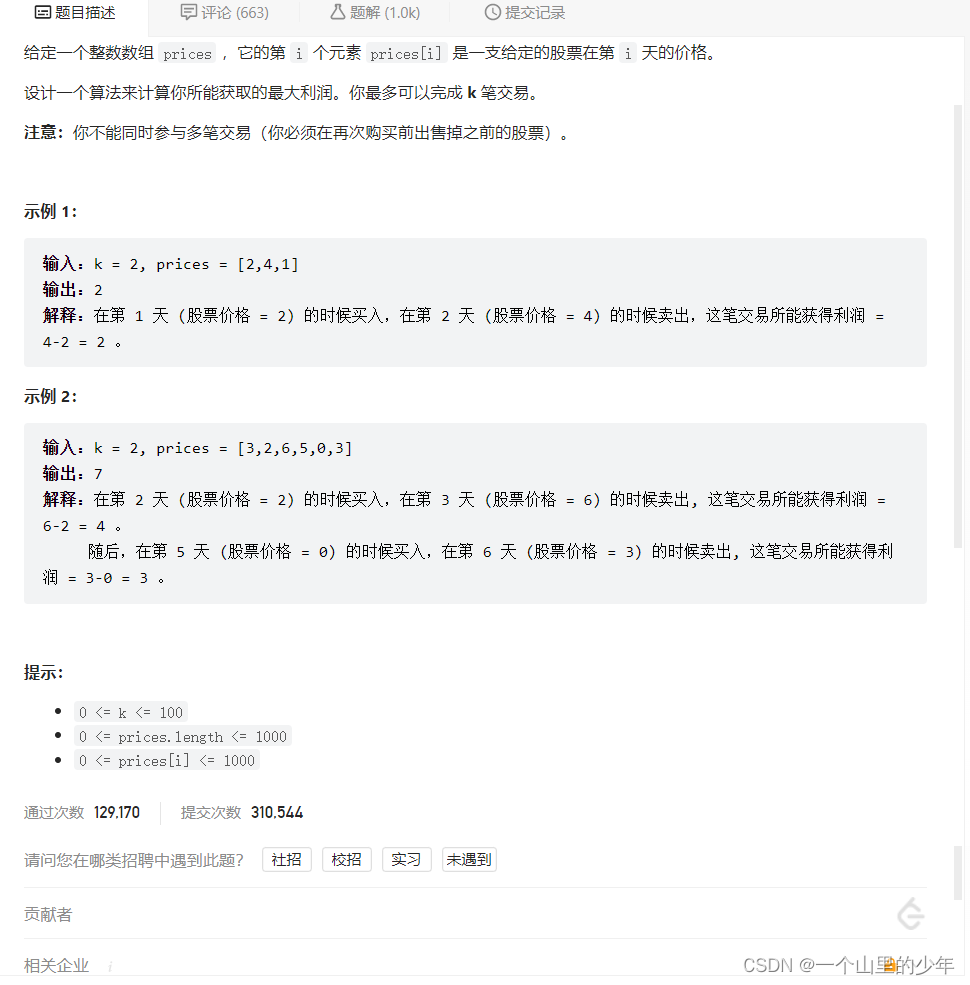
2.题目描述:
3.解题思路:
首先我们先确定模型这是一个从左到右的尝试模型。所以我们可以定义一个定义递归函数process:
int process(vector<int>&nums,int index,int k);递归含义是数组nums[0.....index]范围内最多交易k次能够获得的最大收益。下面我们来分析可能性:
1.index位置的数要参与交易那么只能在index位置卖出。但是买入时机可以是[0....index]中的任何一个时候。所以我们需要枚举所有可能。
2.index位置的数不参与交易那么最大利润就是[0....index-1]范围内进行交易。
4.对应代码:
class Solution { public: int maxProfit(int k, vector<int>& prices) { if(prices.empty()){ return 0; } return process(prices,prices.size()-1,k); } //递归含义[0....index]范围内最多交易k次能够获得的最大例如 int process(vector<int>&nums,int index,int k){ if(index==0){ return 0; } if(k==0){ return 0; } //可能性1:index位置的数不参与交易 int p1=process(nums,index-1,k); //可能性2:index位置的数参与交易那么只能在index位置时卖出 //但是买入时机可能有多种可能[0.....index]范围内每个位置都可以买入 int p2=0; for(int i=index;i>=0;i--){ p2=max(p2,process(nums,i,k-1)+nums[index]-nums[i]); } return max(p1,p2); } };
对应记忆化搜索版本:
class Solution { public: vector<vector<int>>dp; int maxProfit(int k, vector<int>& prices) { if(prices.empty()){ return 0; } dp.resize(prices.size(),vector<int>(k+1,-1)); return process(prices,prices.size()-1,k); } //递归含义[0....index]范围内最多交易k次能够获得的最大例如 int process(vector<int>&nums,int index,int k){ if(index==0){ return 0; } if(k==0){ return 0; } if(dp[index][k]!=-1){ return dp[index][k]; } //可能性1:index位置的数不参与交易 int p1=process(nums,index-1,k); //可能性2:index位置的数参与交易那么只能在index位置时卖出 //但是买入时机可能有多种可能[0.....index]范围内每个位置都可以买入 int p2=0; for(int i=index;i>=0;i--){ p2=max(p2,process(nums,i,k-1)+nums[index]-nums[i]); } int ans= max(p1,p2); dp[index][k]=ans;//缓存 return ans; } };
对应严格位置依赖的dp:
class Solution { public: int maxProfit(int k, vector<int>& nums) { if(nums.empty()){ return 0; } int N=nums.size(); vector<vector<int>>dp(N,vector<int>(k+1)); //动态规划的版本由暴力递归改出来 for(int i=1;i<N;i++){ for(int j=1;j<=k;j++){ int p1=dp[i-1][j]; int p2=0; for(int t=i;t>=0;t--){ p2=max(p2,dp[t][j-1]+nums[i]-nums[t]); } dp[i][j]=max(p1,p2); } } return dp[N-1][k]; } //递归含义[0....index]范围内最多交易k次能够获得的最大例如 int process(vector<int>&nums,int index,int k){ if(index==0){ return 0; } if(k==0){ return 0; } //可能性1:index位置的数不参与交易 int p1=process(nums,index-1,k); //可能性2:index位置的数参与交易那么只能在index位置时卖出 //但是买入时机可能有多种可能[0.....index]范围内每个位置都可以买入 int p2=0; for(int i=index;i>=0;i--){ p2=max(p2,process(nums,i,k-1)+nums[index]-nums[i]); } int ans= max(p1,p2); return ans; } };
斜率优化:
当我们发现在严格位置依赖的动态规划当中发现了有枚举行为。此时我们可以进行斜率优化。下面我们来举一个例子比如说我们要求dp[5][2]:
可能性1:5位置的值不参与那么就是dp[4][2].
可能性2:5位置的数要参与那么就只能是卖出时机。而买入时机有很多首先是5位置买入5位置卖出:dp[5][2]=
dp[5][1]+nums[5]-nums[5].
4位置买入5位置卖出:
dp[4][1]+nums[5]-nums[4];
3位置买入5位置卖出:
dp[3][1]+nums[5]-nums[3];
2位置买入5位置卖出:
dp[2][1]+nums[5]-nums[2];
那么dp[5][2]的值就是这几种可能性中求最大即可
下面我们同理按照上述方法看看dp[6][2].
情况一:6位置的数不参与交易
dp[6][2]=dp[5][2];
情况二:6位置的数参与交易那么就必须是卖出时机
同理dp[6][1]+nums[6]-nums[6];
dp[5][1]+nums[6]-nums[5];
dp[4][1]+nums[6]-nums[4];
dp[3][1]+nums[6]-nums[3];
..............
下面我们来看看dp[5][2]列出来的状态能不能简化dp[6][2]列出来的状态。看起来好像dp[5][2]的状态无法优化dp[6][2]的状态。但是如果我们在求dp[5][2]的时候暂时不加哪个nums[5],而是先求出这么多可能性中哪个最大,将最大的哪个加上nums[5]。这样dp[5][2]的状态不就可以优化dp[6][2]吗
对应斜率优化代码:
class Solution { public: int maxProfit(int k, vector<int>& nums) { if (nums.size() < 2) { return 0; } int N = nums.size(); vector<vector<int>>dp(N, vector<int>(k + 1)); for (int j = 1; j <= k; j++) { //需要先填写第一行的值才能优化后面的 int p1 = dp[0][j]; int best = max(dp[1][j - 1] - nums[1], dp[0][j - 1] - nums[0]); dp[1][j] = max(best + nums[1], p1); for (int i = 2; i < N; i++) { int curA = dp[i - 1][j]; int a = dp[i][j - 1] - nums[i]; best = max(best, a); dp[i][j] = max(curA, best + nums[i]); } } return dp[N - 1][k]; } //递归含义[0....index]范围内最多交易k次能够获得的最大例如 int process(vector<int>& nums, int index, int k) { if (index == 0) { return 0; } if (k == 0) { return 0; } //可能性1:index位置的数不参与交易 int p1 = process(nums, index - 1, k); //可能性2:index位置的数参与交易那么只能在index位置时卖出 //但是买入时机可能有多种可能[0.....index]范围内每个位置都可以买入 int p2 = 0; for (int i = index; i >= 0; i--) { p2 = max(p2, process(nums, i, k - 1) + nums[index] - nums[i]); } int ans = max(p1, p2); return ans; } };