目录
题目介绍
题目链接
题目描述
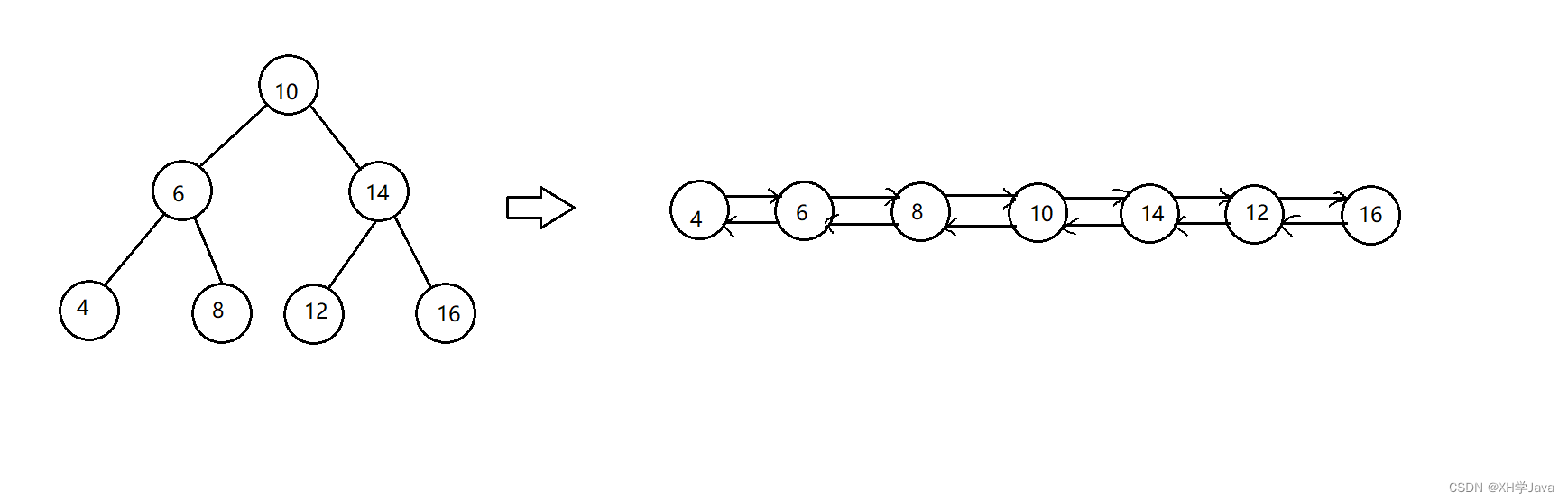
输入一颗二叉搜索树,将该二叉搜索树转换为一个排序的双向链表
如:
题目要求及数据范围
数据范围:输入二叉树的结点数0 <= n <= 1000,二叉树中每个结点的值0 <= val <= 1000
要求:空间复杂度为O(1),时间复杂度O(n)
题目注意事项
要求不能创建新的结点,只能调整树中的结点指向,树中结点的左指针指向前驱,右指针指向后继
返回链表中第一个结点的指针
函数返回的TreeNode,有左右指针,其实可以看成一个双向链表
不用输出双向链表,程序会根据返回值自动打印输出
二叉搜索树性质介绍
二叉搜索树又称二叉排序树,它具有以下性质:
- 若它的左子树不为空,则左子树结点的值都小于根结点的值
- 若它的右子树不为空,则右子树结点的值都大于根结点的值
- 它的左右子树也是二叉搜索树
题目分析
题目要将一颗二叉搜索树转化为一个有序的双向链表,从上面二叉搜索树的性质不难得出,该二叉搜索树的中序遍历出的结果刚好是从小到大的顺序,题目要求结点的left指针指向前驱,right指针指向后继,故做题思路如下:
将中序遍历的结点根据题目要求链接起来
解题方法
方法一
画图分析过程:
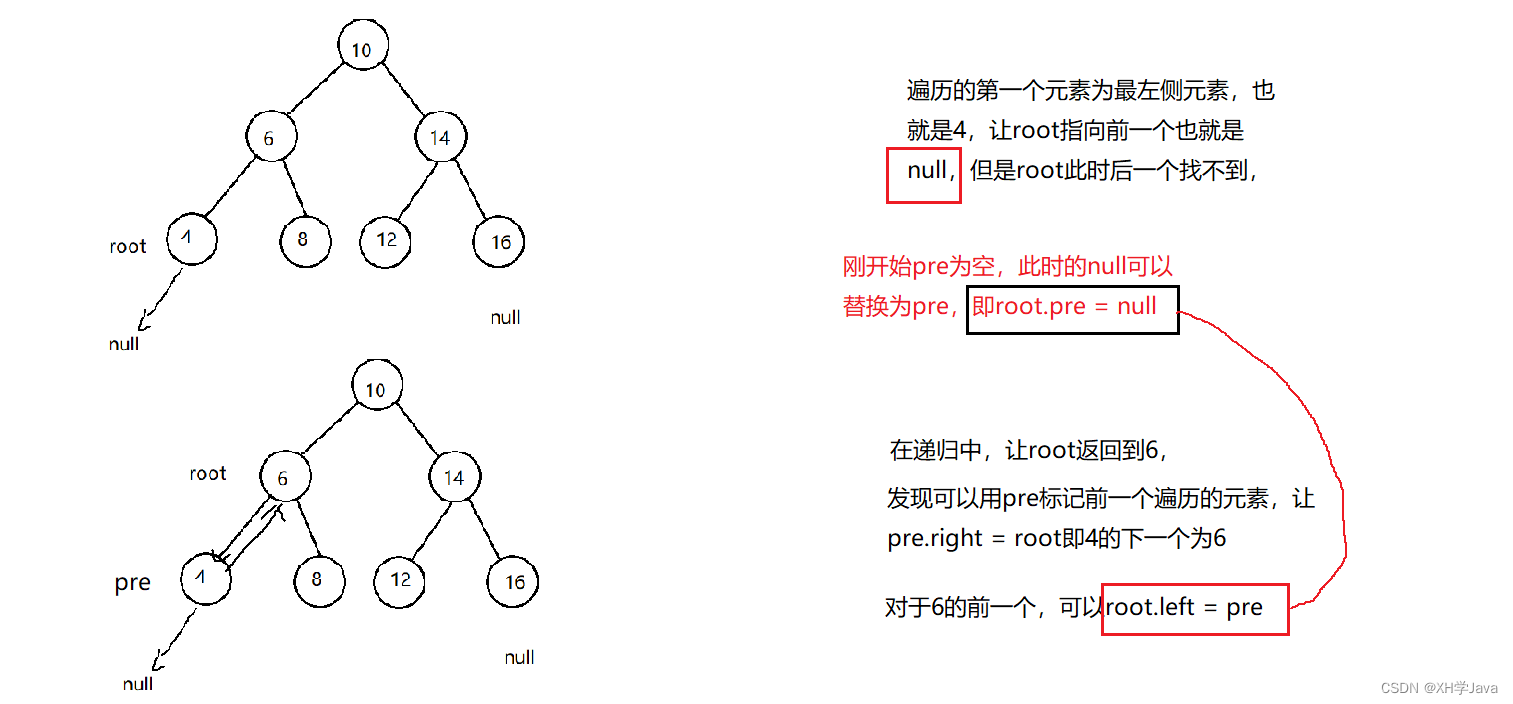
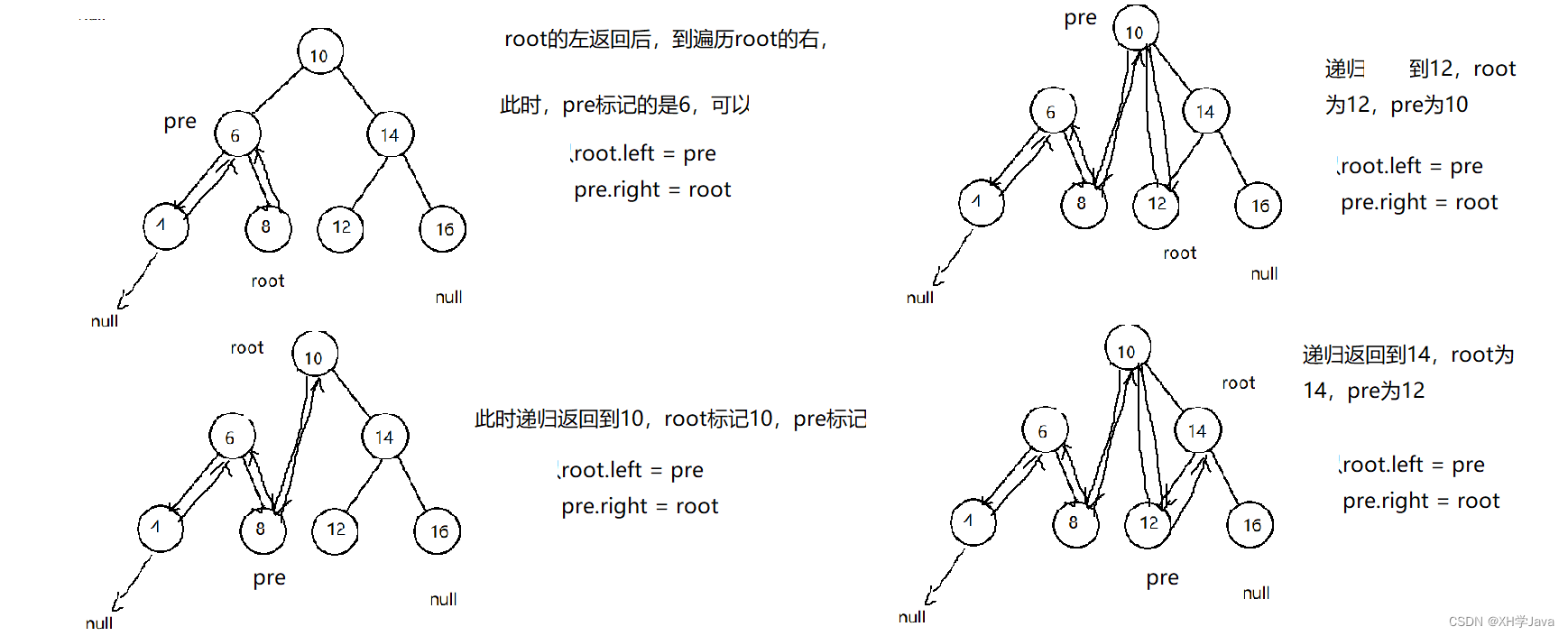
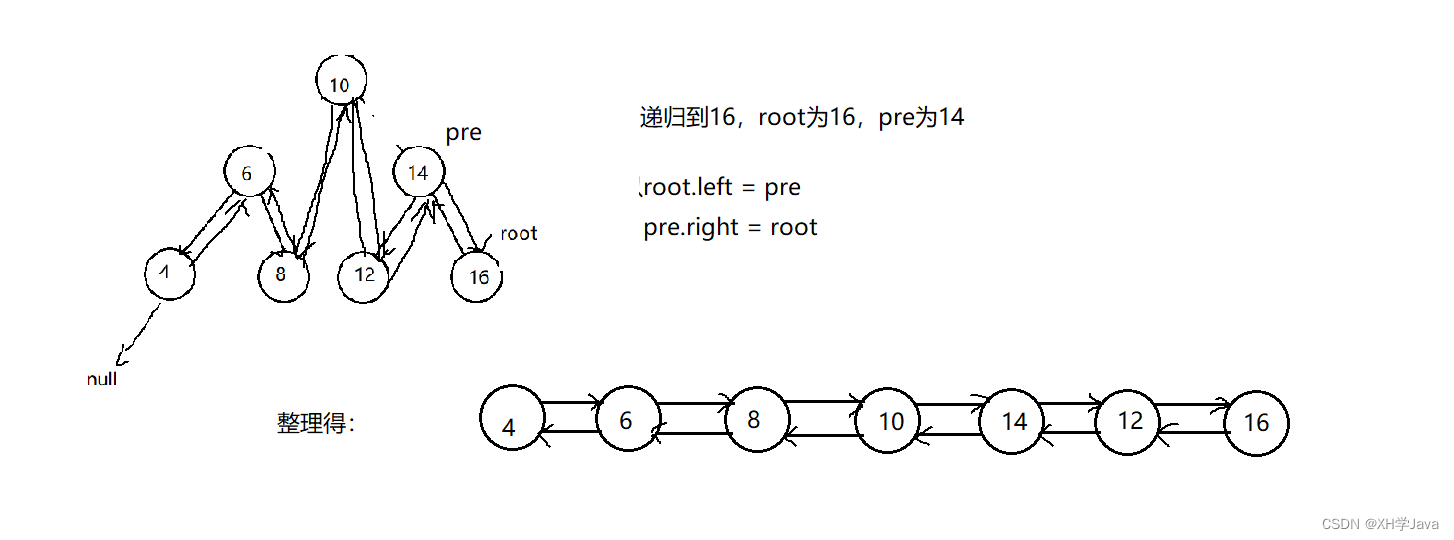
具体步骤如下:
- 写一个中序遍历的方法,链接结点
- 中序遍历采用递归实现,所以在方法外侧先定义pre==null,pre标记遍历root时前一个结点
- 先递归遍历左子树
- 再让root.left == pre,if(pre != null)时,让pre.right = root
- 最后递归遍历右子树
- 题目给出的方法要返回首结点,首结点为该树的最左侧结点,先找到首结点
- 如果树为空,返回null,如果不为空,如果根的左子树不为空,在以根的左子树为树继续找最左侧的结点
- 调用上述中序遍历方法
- 返回首结点
方法二
因为题目给出了结点的最大个数为1000,并且要求空间复杂度为O(1),所以我们可以将中序遍历的结点存入一个数组中,该数组new空间的大小为1000,因为1000为具体数值,所以空间复杂度也满足O(1),再遍历数组将数组中的结点链接起来
具体步骤如下:
- new空间为1000存放结点的数组
- 写一个中序遍历将树中所有的结点存入数组中
- 在题目给出的方法中,先调用上述方法,将结点存入数组中
- 从index=0开始遍历数组,让array[index+1].left = array[index],array[index].right = array[index+1]
代码实现
方法一代码
import java.util.*;
/**
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
public class Solution {
TreeNode pre = null;
public void inOrder(TreeNode root){
if(root == null){
return;
}
inOrder(root.left);
root.left = pre;
if(pre != null){
pre.right = root;
}
pre = root;
inOrder(root.right);
}
public TreeNode Convert(TreeNode pRootOfTree) {
if(pRootOfTree == null){
return null;
}
TreeNode head = pRootOfTree;
while(head.left != null){
head = head.left;
}
inOrder(pRootOfTree);
return head;
}
}方法二代码
import java.util.*;
/**
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
public class Solution {
TreeNode[] array = new TreeNode[1000];
int i = 0;
public void inOrder(TreeNode root){
if(root != null){
inOrder(root.left);
array[i++] = root;
inOrder(root.right);
}
}
public TreeNode Convert(TreeNode pRootOfTree) {
inOrder(pRootOfTree);
int index = 0;
while(array[index+1] != null){
array[index].right = array[index+1];
array[index+1].left = array[index];
index++;
}
return array[0];
}
}