一种改进的蝴蝶优化算法
文章目录
摘要:蝴蝶优化算法作为新提出的自然启发算法,其寻优方式模拟了蝴蝶利用嗅觉来确定花蜜或交配对象位置的行为。针对蝴蝶优化算法求解精度不高和收敛速度慢等问题,提出一种基于自适应扰动的疯狂蝴蝶算法(CIBOA)。首先,在自身认知飞行部分引入自适应惯性权重,平衡算法的局部与全局搜索能力;其次,在全局最优位置引入扰动策略,避免算法陷入局部最优;最后,在花蜜位置引入疯狂因子以增加种群多样性,获取更好的最优解。
1.蝴蝶优化算法
基础蝴蝶优化算法的具体原理参考,我的博客:https://blog.csdn.net/u011835903/article/details/107855860
2. 改进蝴蝶优化算法
2.1 自适应惯性权重
在 BOA 的自身认知飞行部分体现了后置蝴蝶追随前一只 蝴蝶位置的能力。文献 [13] 在 PSO 算法中引入惯性权重 ω \omega ω, 分析指出: 惯性权重较大或较小都有可能引起算法陷入局部最 优, 从而影响算法效率。为了更好地平衡算法的局部与全局搜 索能力, 本文引入线性递减的惯性权重来更新蝴蝶的位置, 表 示为
x i t = { ω ( t ) × x i t + ( r 1 2 × g ∗ − x i t ) × f i r 3 ⩽ P ω ( t ) × x i t + ( r 2 2 × x j t − x k t ) × f i r 3 > P ω ( t ) = ω min + ( ω max − ω min ) exp ( − 0.5 × ( t t max ) 2 ) \begin{array}{r} \boldsymbol{x}_{i}^{t}=\left\{\begin{array}{rr} \omega(t) \times \boldsymbol{x}_{i}^{t}+\left(r_{1}^{2} \times g^{*}-\boldsymbol{x}_{i}^{t}\right) \times f_{i} & r_{3} \leqslant P \\ \omega(t) \times \boldsymbol{x}_{i}^{t}+\left(r_{2}^{2} \times \boldsymbol{x}_{j}^{t}-\boldsymbol{x}_{k}^{t}\right) \times f_{i} & r_{3}>P \end{array}\right. \\ \omega(t)=\omega_{\min }+\left(\omega_{\max }-\omega_{\min }\right) \exp \left(-0.5 \times\left(\frac{t}{t_{\max }}\right)^{2}\right) \end{array} xit={
ω(t)×xit+(r12×g∗−xit)×fiω(t)×xit+(r22×xjt−xkt)×fir3⩽Pr3>Pω(t)=ωmin+(ωmax−ωmin)exp(−0.5×(tmaxt)2)
其中: r 3 r_{3} r3 是 [ 0 , 1 ] [0,1] [0,1] 的随机数; ω max \omega_{\text {max }} ωmax 为初始惯性权重; ω min \omega_{\text {min }} ωmin 为迭代结 束时的惯性权重; t t t 为当前迭代次数; T max T_{\text {max }} Tmax 为最大迭代次数。惯 性权重 ω max = 0.9 , ω min = 0.4 \omega_{\text {max }}=0.9, \omega_{\min }=0.4 ωmax =0.9,ωmin=0.4 时算法具有最佳性能。因此, 随 着迭代的进行, 惯性权重从 0.9 0.9 0.9 线性递减至 0.4 0.4 0.4, 迭代初始阶 段较大的惯性权重让算法保持较好的搜索能力, 而迭代后期较 小的惯性权重有助于算法进行更好的开发能力。
2.2 扰动策略
在 BOA 算法的全局搜索阶段,所有蝴蝶个体都向同一个全局最优位置飞行,这样操作的不足之处在于很容易陷入局部最优,致使该算法在应用于较复杂的多峰函数中时,收敛过早和精度低下的缺点比较明显。对此本文引入文献[11]提出的多段扰动策略用于更新最优花蝊位置 g ∗ g^{*} g∗, 即对全局最优花蝊 位置根据方差可调的正态随机分布进行扰动得到新的全局最 优花蝊位置 g best g_{\text {best }} gbest , 更新公式为
g best = N ( g ∗ , δ ) g_{\text {best }}=N\left(g^{*}, \delta\right) gbest =N(g∗,δ)
其中: δ \delta δ 表示相对于 g ∗ g^{*} g∗ 的不确定度, 是对迭代次数 t t t 的非增函 数,其更新公式为
δ = { δ 1 t < α 1 T δ 2 α 1 T < t < α 2 T δ 3 t > α 2 T \delta= \begin{cases}\delta_{1} & t<\alpha_{1} T \\ \delta_{2} & \alpha_{1} T<t<\alpha_{2} T \\ \delta_{3} & t>\alpha_{2} T\end{cases} δ=⎩
⎨
⎧δ1δ2δ3t<α1Tα1T<t<α2Tt>α2T
其中: δ \delta δ 表示正态扰动的半径参数且 δ 1 > δ 2 > δ 3 ; α 1 、 α 2 \delta_{1}>\delta_{2}>\delta_{3} ; \alpha_{1} 、 \alpha_{2} δ1>δ2>δ3;α1、α2 是半径 变化的控制参数, 且 α 1 < α 2 ; t \alpha_{1}<\alpha_{2} ; t α1<α2;t 是当前迭代次数; T T T 是最大迭代 次数。
2.3 疯狂因子
蝴蝶在飞行的过程中, 其产生的香味大小不可能一直保持 不变, 随着距离浓度的改变来扰乱种群的意外行为。在此用疯 狂因素来描述, 其核心思想是通过疯狂变量对其进行建模, 在 B O A \mathrm{BOA} BOA 的位置公式中引入一个疯狂因子 [ 12 ] { }^{[12]} [12], 确保蝴蝶具有预定 确定的疯狂概率, 以保持种群的多样性, 更新公式为
x i t = { ω ( t ) × x i t + ( r 1 2 × g best − x i t ) × f i + P ( r 4 ) sign ( r 4 ) x craziness r 3 ⩽ P ω ( t ) × x i t + ( r 2 2 × x j t − x k t ) × f i + P ( r 4 ) sign ( r 4 ) x craziness r 3 > P \boldsymbol{x}_{i}^{t}= \begin{cases}\omega(t) \times \boldsymbol{x}_{i}^{t}+\left(r_{1}^{2} \times g_{\text {best }}-\boldsymbol{x}_{i}^{t}\right) \times f_{i}+ & \\ P\left(r_{4}\right) \operatorname{sign}\left(r_{4}\right) x_{\text {craziness }} & r_{3} \leqslant P \\ \omega(t) \times \boldsymbol{x}_{i}^{t}+\left(r_{2}^{2} \times \boldsymbol{x}_{j}^{t}-\boldsymbol{x}_{k}^{t}\right) \times f_{i}+ & \\ P\left(r_{4}\right) \operatorname{sign}\left(r_{4}\right) x_{\text {craziness }} & r_{3}>P\end{cases} xit=⎩
⎨
⎧ω(t)×xit+(r12×gbest −xit)×fi+P(r4)sign(r4)xcraziness ω(t)×xit+(r22×xjt−xkt)×fi+P(r4)sign(r4)xcraziness r3⩽Pr3>P
其中: ω ( t ) \omega(t) ω(t) 表示引入自适应惯性权重; g best g_{\text {best }} gbest 表示引入扰动策略; r 4 r_{4} r4 是 [ 0 , 1 ] [0,1] [0,1] 的随机数; x craziness x_{\text {craziness }} xcraziness 通常取较小的常数; P ( r 4 ) P\left(r_{4}\right) P(r4) 和 sign ( r 4 ) \operatorname{sign}\left(r_{4}\right) sign(r4) 定义分别为
P ( r 4 ) = { 1 if r 4 ⩽ P c r 0 else sign ( r 4 ) = { − 1 if r 4 ⩾ 0.5 1 else \begin{aligned} P\left(r_{4}\right) &= \begin{cases}1 & \text { if } r_{4} \leqslant P_{c r} \\ 0 & \text { else }\end{cases} \\ \operatorname{sign}\left(r_{4}\right) &= \begin{cases}-1 & \text { if } r_{4} \geqslant 0.5 \\ 1 & \text { else }\end{cases} \end{aligned} P(r4)sign(r4)={
10 if r4⩽Pcr else ={
−11 if r4⩾0.5 else
其中: P c r P_{c r} Pcr 为设定的疯狂 概率; x craziness x_{\text {craziness }} xcraziness 为一个非 常小的值 (为 0.0001 0.0001 0.0001 ), 蝴蝶在飞行过程中花䘺位置发生移动的可能性较 小。在这种情况下, 如果 P c r P_{c r} Pcr 取值较小 (为 0.3 0.3 0.3 ), 则随机数 c 4 c_{4} c4 将 有很大概率大于 P c r P_{c r} Pcr, 疯狂因子 P ( c 4 ) P\left(c_{4}\right) P(c4) 也将为 0 , 这是人们实际期 望的。
自适应扰动的 CIBOA 步骤如下:
a) 设置算法参数, 初始化蝴蝶个体位置。根据搜索空间 的上下限, 随机生成一个 N × d N \times d N×d 维矩。
b)计算初始适应度值。根据测试函数计算 N N N 只蝴蝶的适 应度值。
c) 选定花蜜源。把步骤b)中计算后的适应度值进行升序 排列, 适应度值最好的蝴蝶位置选定为花蜜源位置, 并根据 式(1)计算其香味大小。
d) 蝴蝶位置更新。根据式 (8) 和 P P P 值判断当前迭代进行 全局搜索还是局部搜索, 然后对应更新每只蝴蝶的位置。
e) 计算适应值。计算更新后每只蝴蝶所处位置的适应度 值, 并更新最优位置。
f)重复步骤 d) ∼ \sim ∼ e)的更迭过程, 如果达到设置的精度要 求或规定的最大迭代次数, 则终止算法, 输出全局最优解。
3.实验结果
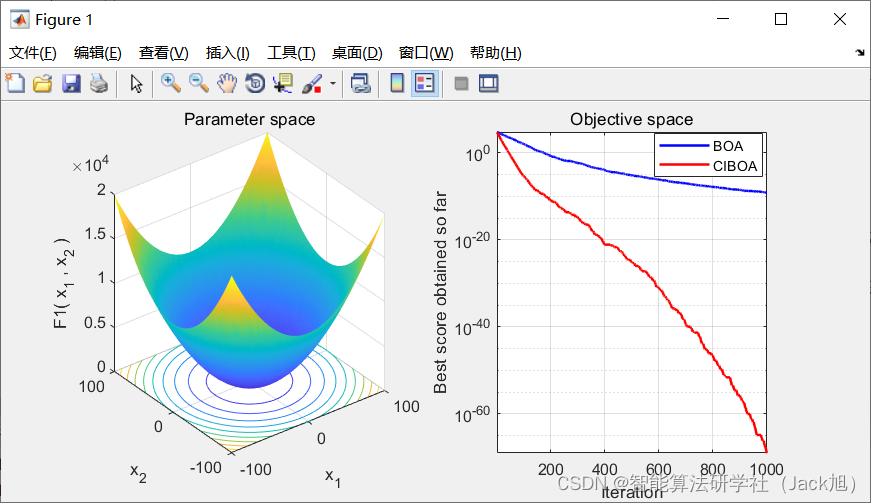
4.参考文献
[1]王依柔,张达敏,徐航,宋婷婷,樊英.基于自适应扰动的疯狂蝴蝶算法[J].计算机应用研究,2020,37(11):3276-3280.